Constrained Bayesian Optimization with Max-Value Entropy Search
Paper and Code
Oct 15, 2019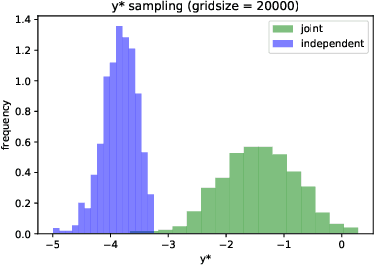
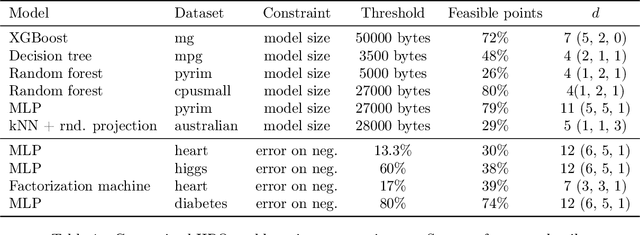
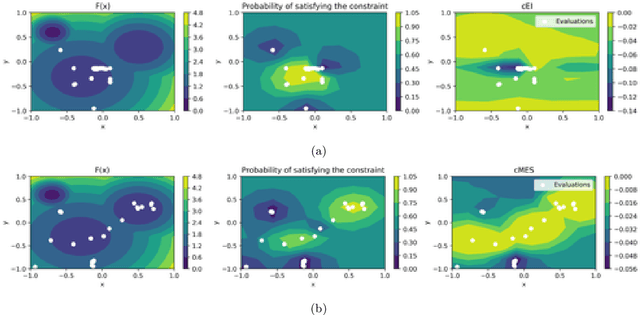
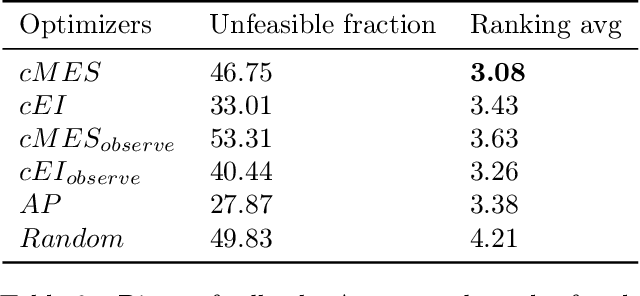
Bayesian optimization (BO) is a model-based approach to sequentially optimize expensive black-box functions, such as the validation error of a deep neural network with respect to its hyperparameters. In many real-world scenarios, the optimization is further subject to a priori unknown constraints. For example, training a deep network configuration may fail with an out-of-memory error when the model is too large. In this work, we focus on a general formulation of Gaussian process-based BO with continuous or binary constraints. We propose constrained Max-value Entropy Search (cMES), a novel information theoretic-based acquisition function implementing this formulation. We also revisit the validity of the factorized approximation adopted for rapid computation of the MES acquisition function, showing empirically that this leads to inaccurate results. On an extensive set of real-world constrained hyperparameter optimization problems we show that cMES compares favourably to prior work, while being simpler to implement and faster than other constrained extensions of Entropy Search.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge