Randomized Asymmetric Chain of LoRA: The First Meaningful Theoretical Framework for Low-Rank Adaptation

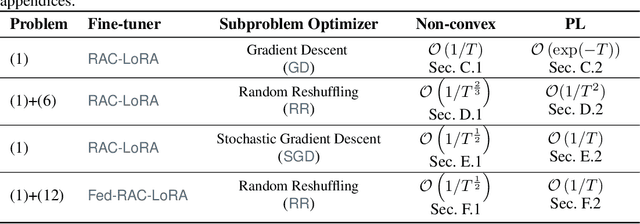
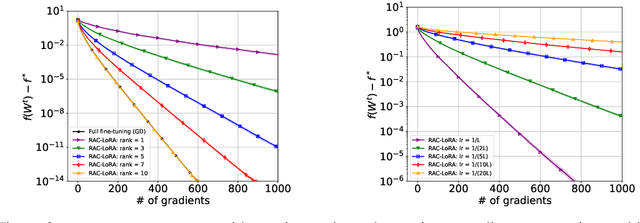
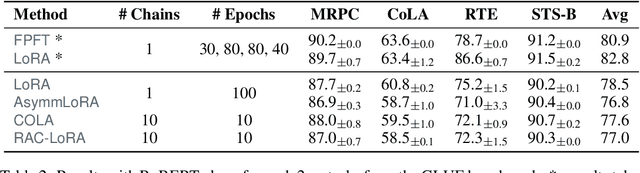
Fine-tuning has become a popular approach to adapting large foundational models to specific tasks. As the size of models and datasets grows, parameter-efficient fine-tuning techniques are increasingly important. One of the most widely used methods is Low-Rank Adaptation (LoRA), with adaptation update expressed as the product of two low-rank matrices. While LoRA was shown to possess strong performance in fine-tuning, it often under-performs when compared to full-parameter fine-tuning (FPFT). Although many variants of LoRA have been extensively studied empirically, their theoretical optimization analysis is heavily under-explored. The starting point of our work is a demonstration that LoRA and its two extensions, Asymmetric LoRA and Chain of LoRA, indeed encounter convergence issues. To address these issues, we propose Randomized Asymmetric Chain of LoRA (RAC-LoRA) -- a general optimization framework that rigorously analyzes the convergence rates of LoRA-based methods. Our approach inherits the empirical benefits of LoRA-style heuristics, but introduces several small but important algorithmic modifications which turn it into a provably convergent method. Our framework serves as a bridge between FPFT and low-rank adaptation. We provide provable guarantees of convergence to the same solution as FPFT, along with the rate of convergence. Additionally, we present a convergence analysis for smooth, non-convex loss functions, covering gradient descent, stochastic gradient descent, and federated learning settings. Our theoretical findings are supported by experimental results.

Synthesizing Mixed-type Electronic Health Records using Diffusion Models

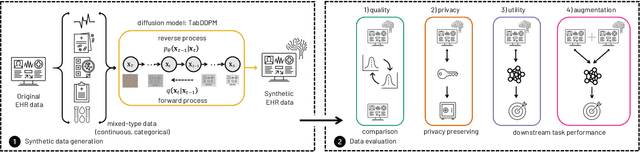
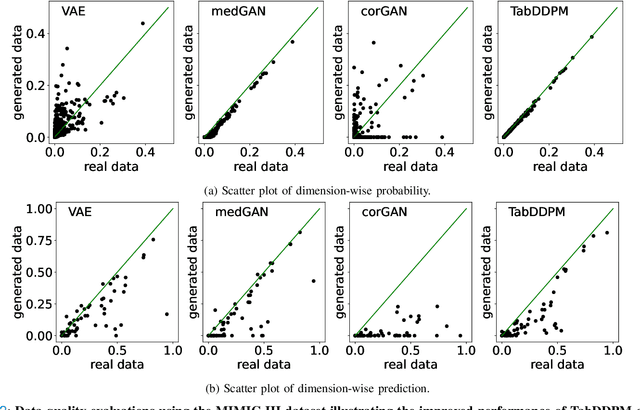
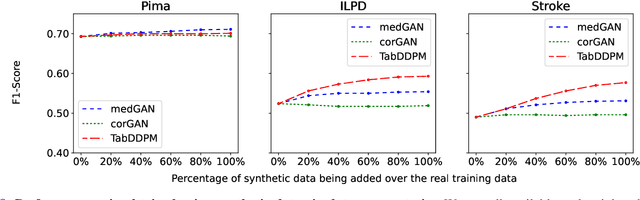
Electronic Health Records (EHRs) contain sensitive patient information, which presents privacy concerns when sharing such data. Synthetic data generation is a promising solution to mitigate these risks, often relying on deep generative models such as Generative Adversarial Networks (GANs). However, recent studies have shown that diffusion models offer several advantages over GANs, such as generation of more realistic synthetic data and stable training in generating data modalities, including image, text, and sound. In this work, we investigate the potential of diffusion models for generating realistic mixed-type tabular EHRs, comparing TabDDPM model with existing methods on four datasets in terms of data quality, utility, privacy, and augmentation. Our experiments demonstrate that TabDDPM outperforms the state-of-the-art models across all evaluation metrics, except for privacy, which confirms the trade-off between privacy and utility.

Mixture of Input-Output Hidden Markov Models for Heterogeneous Disease Progression Modeling

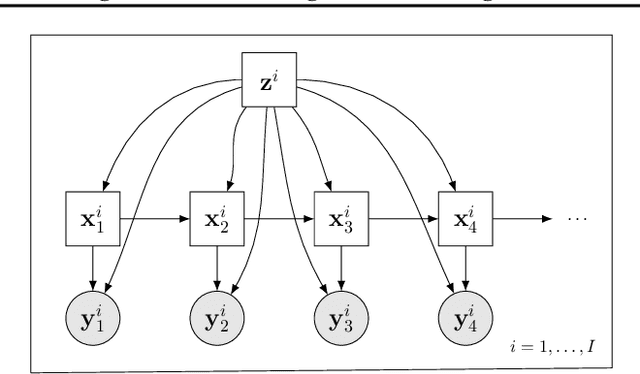
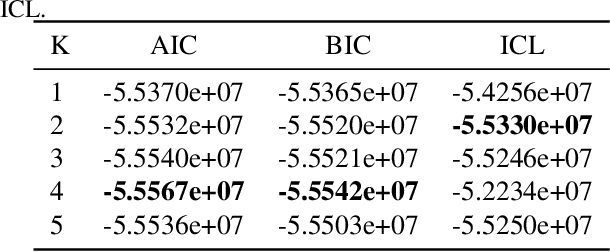
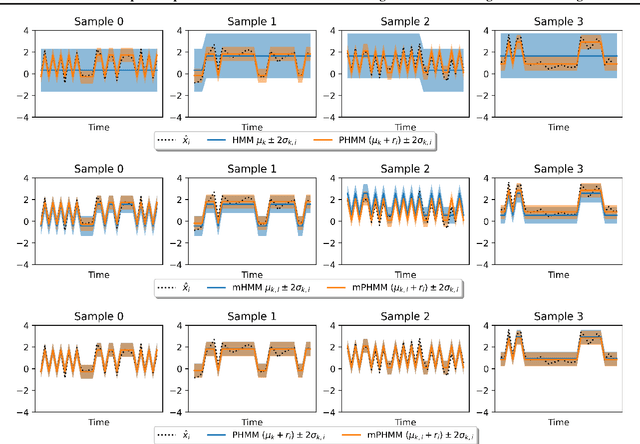
A particular challenge for disease progression modeling is the heterogeneity of a disease and its manifestations in the patients. Existing approaches often assume the presence of a single disease progression characteristics which is unlikely for neurodegenerative disorders such as Parkinson's disease. In this paper, we propose a hierarchical time-series model that can discover multiple disease progression dynamics. The proposed model is an extension of an input-output hidden Markov model that takes into account the clinical assessments of patients' health status and prescribed medications. We illustrate the benefits of our model using a synthetically generated dataset and a real-world longitudinal dataset for Parkinson's disease.

Identifying the Units of Measurement in Tabular Data

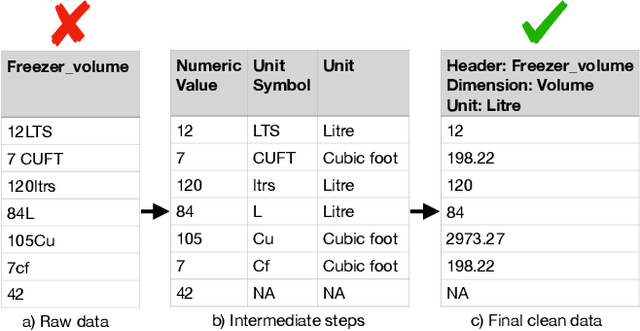
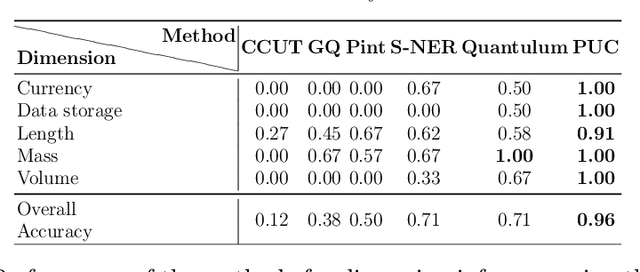
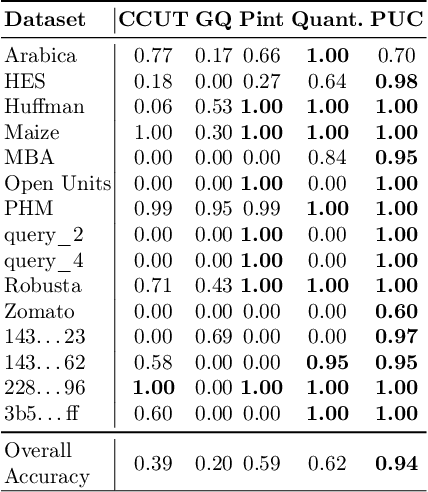
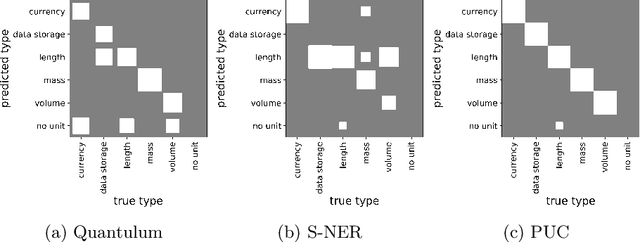
We consider the problem of identifying the units of measurement in a data column that contains both numeric values and unit symbols in each row, e.g., "5.2 l", "7 pints". In this case we seek to identify the dimension of the column (e.g. volume) and relate the unit symbols to valid units (e.g. litre, pint) obtained from a knowledge graph. Below we present PUC, a Probabilistic Unit Canonicalizer that can accurately identify the units of measurement, extract semantic descriptions of quantitative data columns and canonicalize their entries. We present the first messy real-world tabular datasets annotated for units of measurement, which can enable and accelerate the research in this area. Our experiments on these datasets show that PUC achieves better results than existing solutions.

ptype-cat: Inferring the Type and Values of Categorical Variables

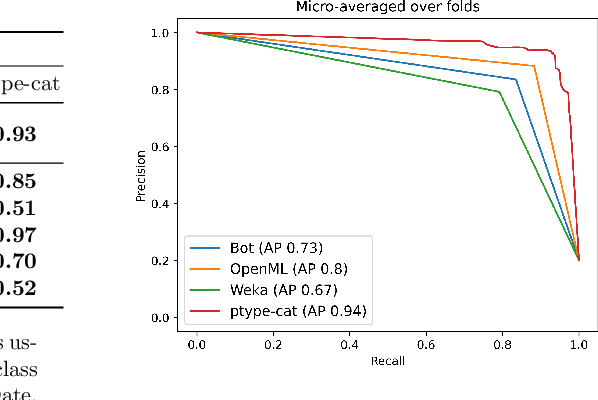
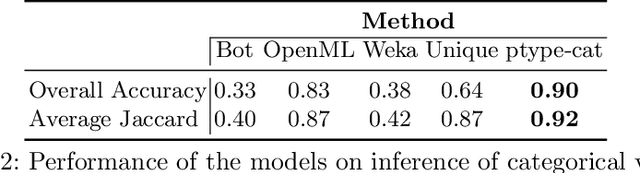
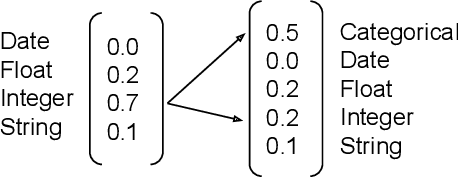
Type inference is the task of identifying the type of values in a data column and has been studied extensively in the literature. Most existing type inference methods support data types such as Boolean, date, float, integer and string. However, these methods do not consider non-Boolean categorical variables, where there are more than two possible values encoded by integers or strings. Therefore, such columns are annotated either as integer or string rather than categorical, and need to be transformed into categorical manually by the user. In this paper, we propose a probabilistic type inference method that can identify the general categorical data type (including non-Boolean variables). Additionally, we identify the possible values of each categorical variable by adapting the existing type inference method ptype. Combining these methods, we present ptype-cat which achieves better results than existing applicable solutions.

ptype: Probabilistic Type Inference

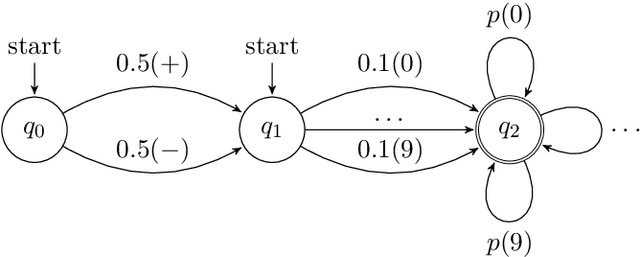
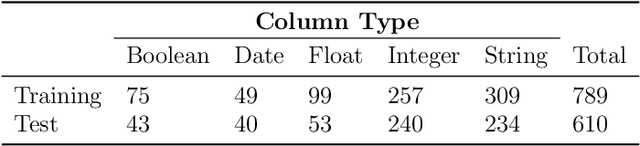
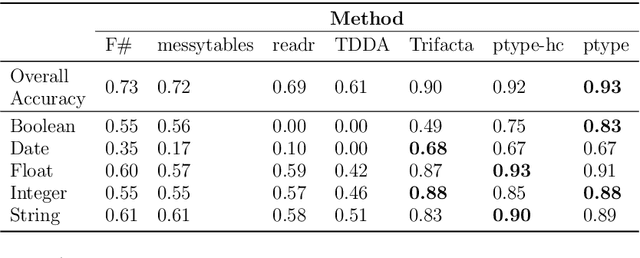
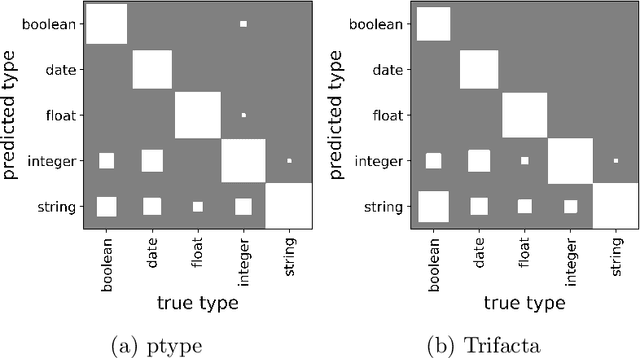
Type inference refers to the task of inferring the data type of a given column of data. Current approaches often fail when data contains missing data and anomalies, which are found commonly in real-world data sets. In this paper, we propose ptype, a probabilistic robust type inference method that allows us to detect such entries, and infer data types. We further show that the proposed method outperforms the existing methods.