Symmetry and Generalisation in Machine Learning

This work is about understanding the impact of invariance and equivariance on generalisation in supervised learning. We use the perspective afforded by an averaging operator to show that for any predictor that is not equivariant, there is an equivariant predictor with strictly lower test risk on all regression problems where the equivariance is correctly specified. This constitutes a rigorous proof that symmetry, in the form of invariance or equivariance, is a useful inductive bias. We apply these ideas to equivariance and invariance in random design least squares and kernel ridge regression respectively. This allows us to specify the reduction in expected test risk in more concrete settings and express it in terms of properties of the group, the model and the data. Along the way, we give examples and additional results to demonstrate the utility of the averaging operator approach in analysing equivariant predictors. In addition, we adopt an alternative perspective and formalise the common intuition that learning with invariant models reduces to a problem in terms of orbit representatives. The formalism extends naturally to a similar intuition for equivariant models. We conclude by connecting the two perspectives and giving some ideas for future work.

Randomized Asymmetric Chain of LoRA: The First Meaningful Theoretical Framework for Low-Rank Adaptation

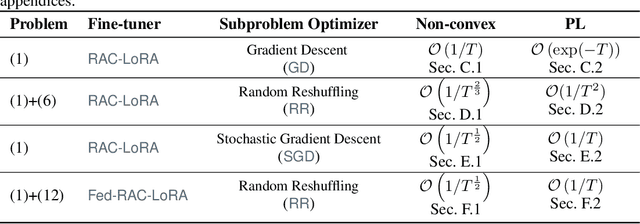
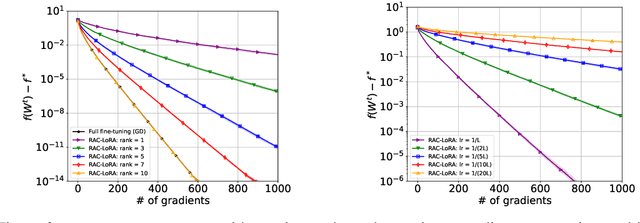
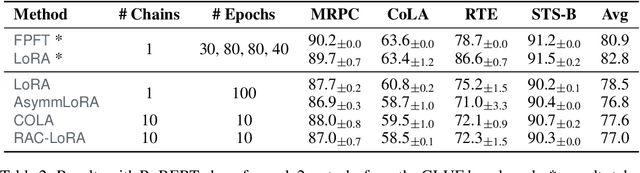
Fine-tuning has become a popular approach to adapting large foundational models to specific tasks. As the size of models and datasets grows, parameter-efficient fine-tuning techniques are increasingly important. One of the most widely used methods is Low-Rank Adaptation (LoRA), with adaptation update expressed as the product of two low-rank matrices. While LoRA was shown to possess strong performance in fine-tuning, it often under-performs when compared to full-parameter fine-tuning (FPFT). Although many variants of LoRA have been extensively studied empirically, their theoretical optimization analysis is heavily under-explored. The starting point of our work is a demonstration that LoRA and its two extensions, Asymmetric LoRA and Chain of LoRA, indeed encounter convergence issues. To address these issues, we propose Randomized Asymmetric Chain of LoRA (RAC-LoRA) -- a general optimization framework that rigorously analyzes the convergence rates of LoRA-based methods. Our approach inherits the empirical benefits of LoRA-style heuristics, but introduces several small but important algorithmic modifications which turn it into a provably convergent method. Our framework serves as a bridge between FPFT and low-rank adaptation. We provide provable guarantees of convergence to the same solution as FPFT, along with the rate of convergence. Additionally, we present a convergence analysis for smooth, non-convex loss functions, covering gradient descent, stochastic gradient descent, and federated learning settings. Our theoretical findings are supported by experimental results.

LoRA-Guard: Parameter-Efficient Guardrail Adaptation for Content Moderation of Large Language Models

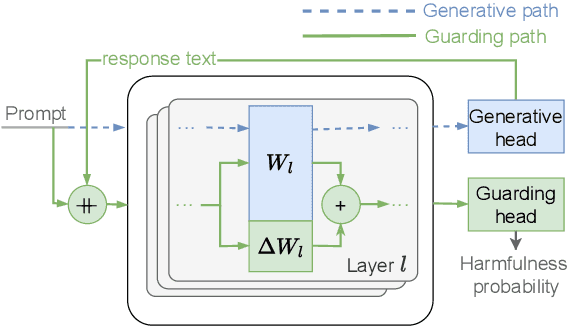
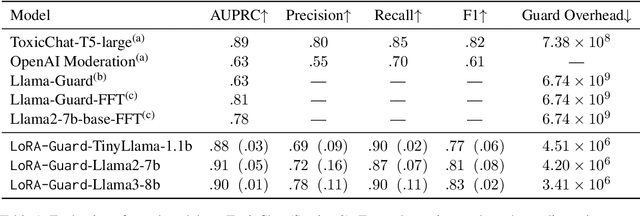
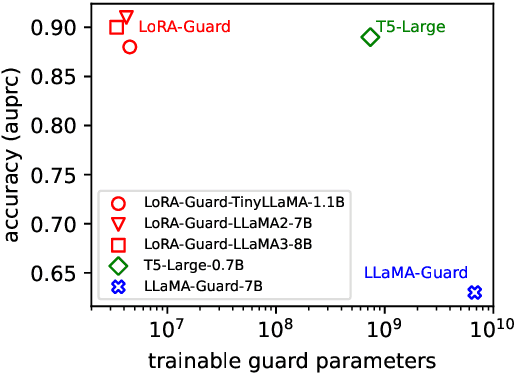
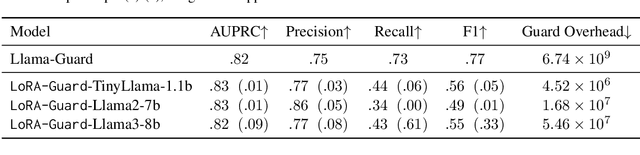
Guardrails have emerged as an alternative to safety alignment for content moderation of large language models (LLMs). Existing model-based guardrails have not been designed for resource-constrained computational portable devices, such as mobile phones, more and more of which are running LLM-based applications locally. We introduce LoRA-Guard, a parameter-efficient guardrail adaptation method that relies on knowledge sharing between LLMs and guardrail models. LoRA-Guard extracts language features from the LLMs and adapts them for the content moderation task using low-rank adapters, while a dual-path design prevents any performance degradation on the generative task. We show that LoRA-Guard outperforms existing approaches with 100-1000x lower parameter overhead while maintaining accuracy, enabling on-device content moderation.