Isometric Representation Learning for Disentangled Latent Space of Diffusion Models

The latent space of diffusion model mostly still remains unexplored, despite its great success and potential in the field of generative modeling. In fact, the latent space of existing diffusion models are entangled, with a distorted mapping from its latent space to image space. To tackle this problem, we present Isometric Diffusion, equipping a diffusion model with a geometric regularizer to guide the model to learn a geometrically sound latent space of the training data manifold. This approach allows diffusion models to learn a more disentangled latent space, which enables smoother interpolation, more accurate inversion, and more precise control over attributes directly in the latent space. Our extensive experiments consisting of image interpolations, image inversions, and linear editing show the effectiveness of our method.

GraphPipe: Improving Performance and Scalability of DNN Training with Graph Pipeline Parallelism

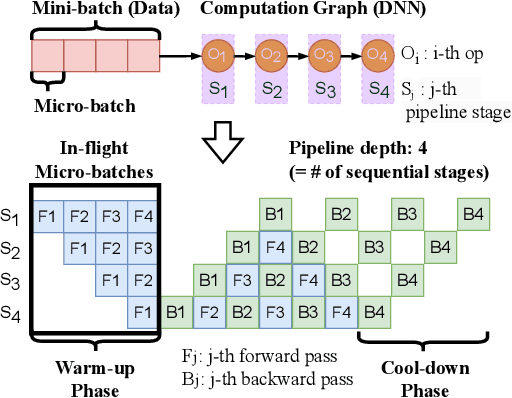
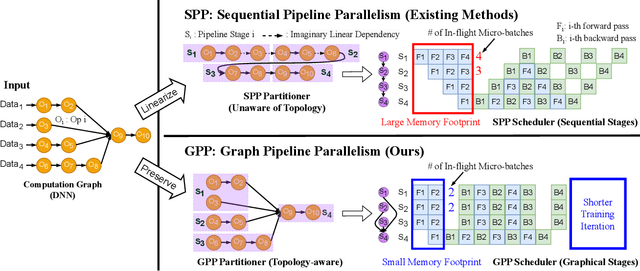
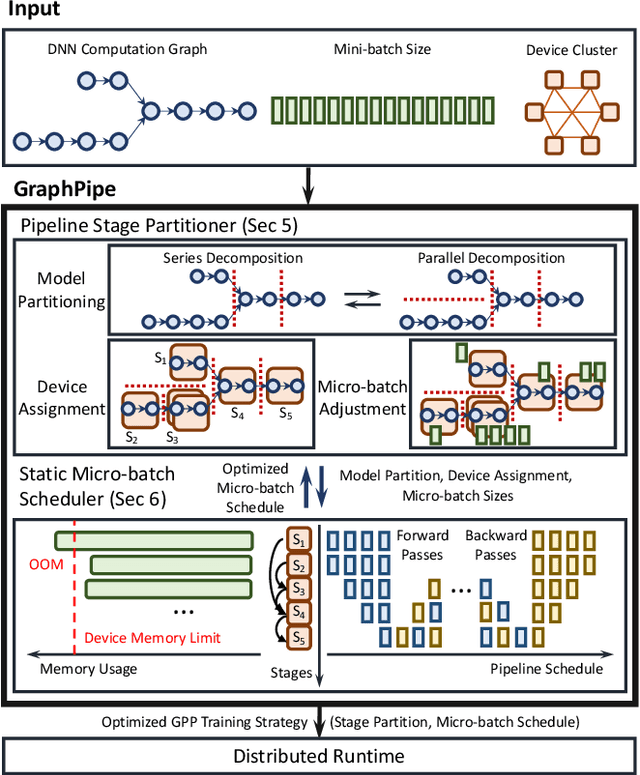
Deep neural networks (DNNs) continue to grow rapidly in size, making them infeasible to train on a single device. Pipeline parallelism is commonly used in existing DNN systems to support large-scale DNN training by partitioning a DNN into multiple stages, which concurrently perform DNN training for different micro-batches in a pipeline fashion. However, existing pipeline-parallel approaches only consider sequential pipeline stages and thus ignore the topology of a DNN, resulting in missed model-parallel opportunities. This paper presents graph pipeline parallelism (GPP), a new pipeline-parallel scheme that partitions a DNN into pipeline stages whose dependencies are identified by a directed acyclic graph. GPP generalizes existing sequential pipeline parallelism and preserves the inherent topology of a DNN to enable concurrent execution of computationally-independent operators, resulting in reduced memory requirement and improved GPU performance. In addition, we develop GraphPipe, a distributed system that exploits GPP strategies to enable performant and scalable DNN training. GraphPipe partitions a DNN into a graph of stages, optimizes micro-batch schedules for these stages, and parallelizes DNN training using the discovered GPP strategies. Evaluation on a variety of DNNs shows that GraphPipe outperforms existing pipeline-parallel systems such as PipeDream and Piper by up to 1.6X. GraphPipe also reduces the search time by 9-21X compared to PipeDream and Piper.

Efficient Strong Scaling Through Burst Parallel Training

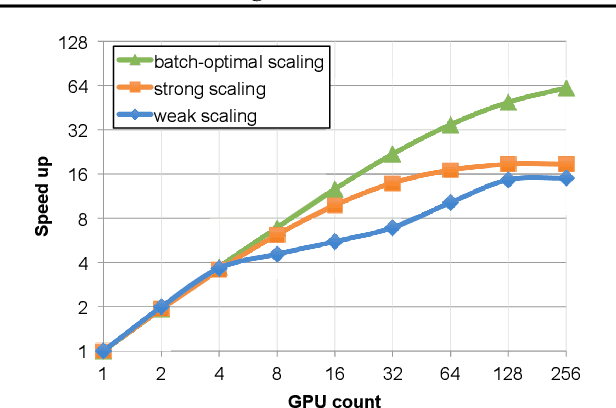
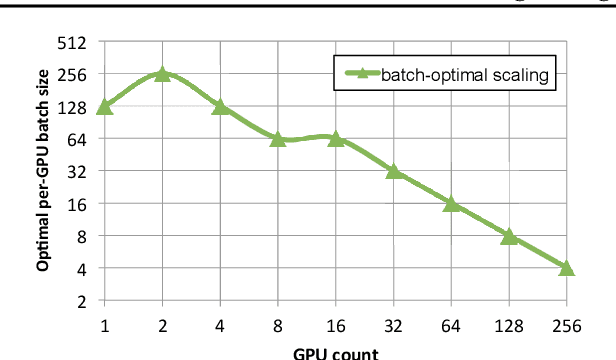
As emerging deep neural network (DNN) models continue to grow in size, using large GPU clusters to train DNNs is becoming an essential requirement to achieving acceptable training times. In this paper, we consider the case where future increases in cluster size will cause the global batch size that can be used to train models to reach a fundamental limit: beyond a certain point, larger global batch sizes cause sample efficiency to degrade, increasing overall time to accuracy. As a result, to achieve further improvements in training performance, we must instead consider "strong scaling" strategies that hold the global batch size constant and allocate smaller batches to each GPU. Unfortunately, this makes it significantly more difficult to use cluster resources efficiently. We present DeepPool, a system that addresses this efficiency challenge through two key ideas. First, burst parallelism allocates large numbers of GPUs to foreground jobs in bursts to exploit the unevenness in parallelism across layers. Second, GPU multiplexing prioritizes throughput for foreground training jobs, while packing in background training jobs to reclaim underutilized GPU resources, thereby improving cluster-wide utilization. Together, these two ideas enable DeepPool to deliver a 2.2 - 2.4x improvement in total cluster throughput over standard data parallelism with a single task when the cluster scale is large.

Top-$K$ Ranking from Pairwise Comparisons: When Spectral Ranking is Optimal

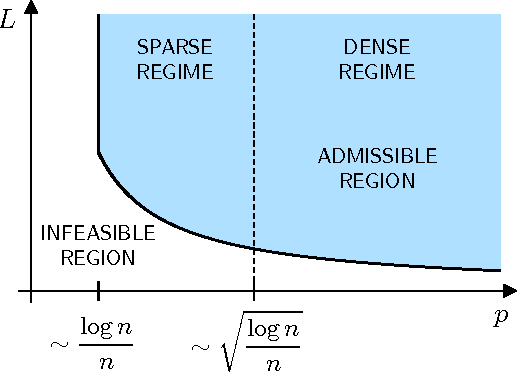
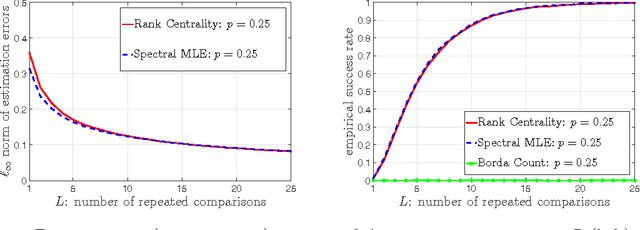
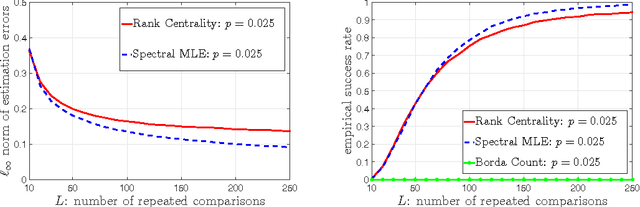
We explore the top-$K$ rank aggregation problem. Suppose a collection of items is compared in pairs repeatedly, and we aim to recover a consistent ordering that focuses on the top-$K$ ranked items based on partially revealed preference information. We investigate the Bradley-Terry-Luce model in which one ranks items according to their perceived utilities modeled as noisy observations of their underlying true utilities. Our main contributions are two-fold. First, in a general comparison model where item pairs to compare are given a priori, we attain an upper and lower bound on the sample size for reliable recovery of the top-$K$ ranked items. Second, more importantly, extending the result to a random comparison model where item pairs to compare are chosen independently with some probability, we show that in slightly restricted regimes, the gap between the derived bounds reduces to a constant factor, hence reveals that a spectral method can achieve the minimax optimality on the (order-wise) sample size required for top-$K$ ranking. That is to say, we demonstrate a spectral method alone to be sufficient to achieve the optimality and advantageous in terms of computational complexity, as it does not require an additional stage of maximum likelihood estimation that a state-of-the-art scheme employs to achieve the optimality. We corroborate our main results by numerical experiments.