Gradient Descent on Logistic Regression with Non-Separable Data and Large Step Sizes

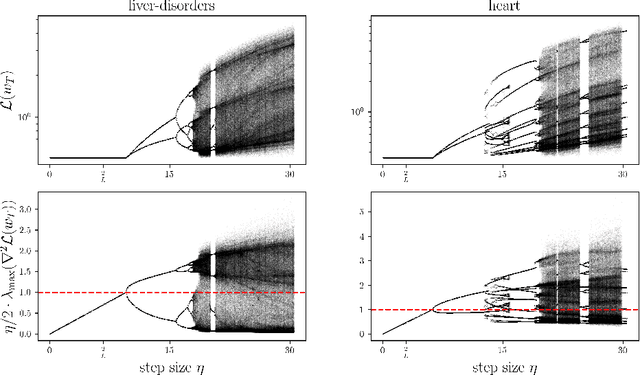
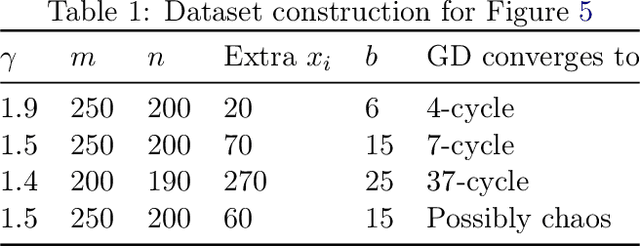
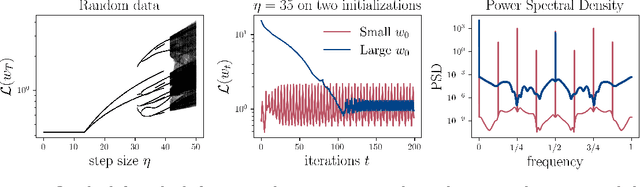
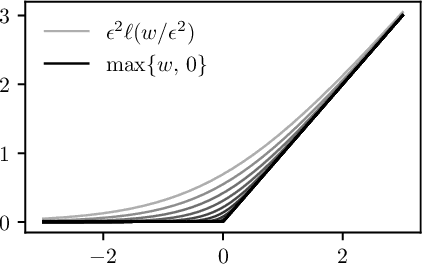
We study gradient descent (GD) dynamics on logistic regression problems with large, constant step sizes. For linearly-separable data, it is known that GD converges to the minimizer with arbitrarily large step sizes, a property which no longer holds when the problem is not separable. In fact, the behaviour can be much more complex -- a sequence of period-doubling bifurcations begins at the critical step size $2/\lambda$, where $\lambda$ is the largest eigenvalue of the Hessian at the solution. Using a smaller-than-critical step size guarantees convergence if initialized nearby the solution: but does this suffice globally? In one dimension, we show that a step size less than $1/\lambda$ suffices for global convergence. However, for all step sizes between $1/\lambda$ and the critical step size $2/\lambda$, one can construct a dataset such that GD converges to a stable cycle. In higher dimensions, this is actually possible even for step sizes less than $1/\lambda$. Our results show that although local convergence is guaranteed for all step sizes less than the critical step size, global convergence is not, and GD may instead converge to a cycle depending on the initialization.

A Model-Based Method for Minimizing CVaR and Beyond

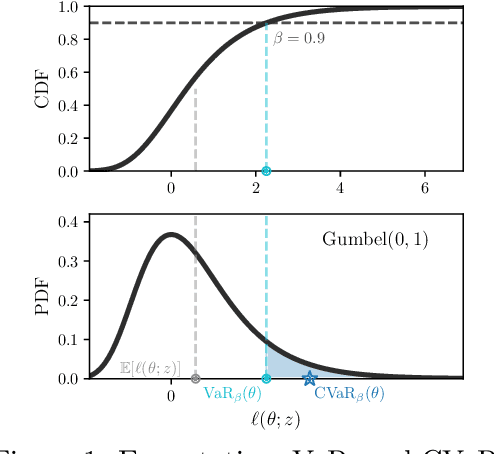
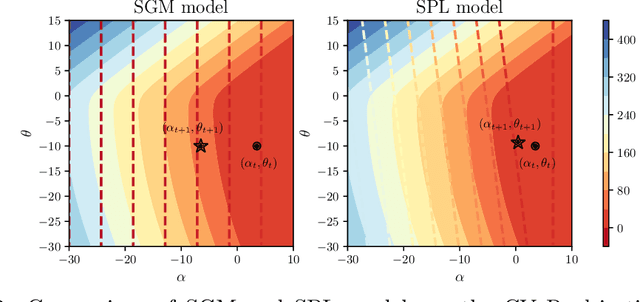
We develop a variant of the stochastic prox-linear method for minimizing the Conditional Value-at-Risk (CVaR) objective. CVaR is a risk measure focused on minimizing worst-case performance, defined as the average of the top quantile of the losses. In machine learning, such a risk measure is useful to train more robust models. Although the stochastic subgradient method (SGM) is a natural choice for minimizing the CVaR objective, we show that our stochastic prox-linear (SPL+) algorithm can better exploit the structure of the objective, while still providing a convenient closed form update. Our SPL+ method also adapts to the scaling of the loss function, which allows for easier tuning. We then specialize a general convergence theorem for SPL+ to our setting, and show that it allows for a wider selection of step sizes compared to SGM. We support this theoretical finding experimentally.

Adaptive Gradient Methods Converge Faster with Over-Parameterization (and you can do a line-search)

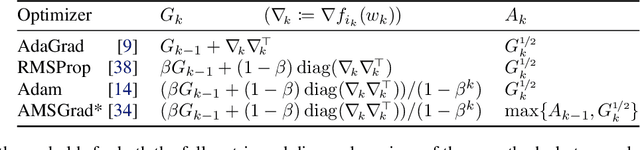
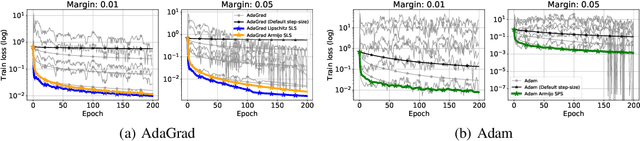
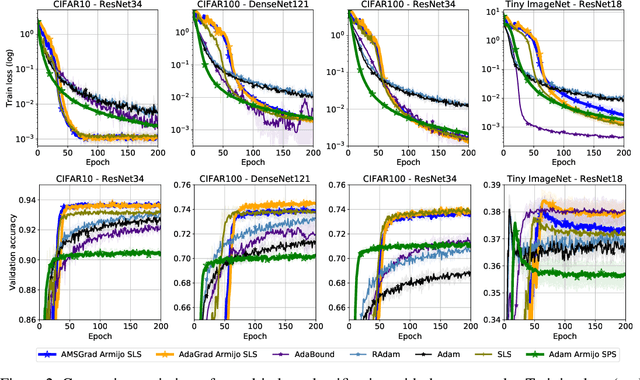
As adaptive gradient methods are typically used for training over-parameterized models capable of exactly fitting the data, we study their convergence in this interpolation setting. Under this assumption, we prove that constant step-size, zero-momentum variants of Adam and AMSGrad can converge to the minimizer at the O(1/T) rate for smooth, convex functions. When this assumption is only approximately satisfied, we show that these methods converge to a neighbourhood of the solution. On the other hand, we show that Adagrad is robust to the violation of interpolation and converges to the minimizer at the optimal rate. However, we demonstrate that even for simple, convex problems satisfying interpolation, the empirical performance of these methods heavily depends on the step-size and requires tuning. We alleviate this problem by making use of stochastic line-search methods (SLS) and Polyak's step-sizes (SPS) to help these methods adapt to the function's local smoothness. We prove that adaptive methods used in conjunction with these techniques do not require knowledge of problem-dependent constants and retain the convergence guarantees of their constant step-size counterparts. Experimentally, we show that using SLS or SPS consistently improves the convergence of adaptive methods across tasks; from binary classification with kernel mappings to classification with deep neural networks. Furthermore, our empirical results show that Adagrad equipped with SLS generalizes better than SGD.

OptiBox: Breaking the Limits of Proposals for Visual Grounding

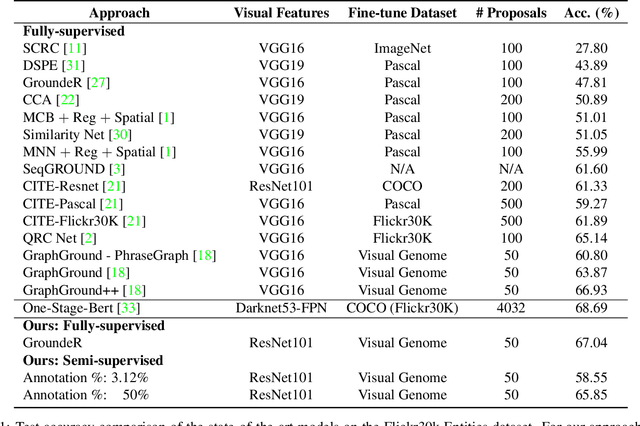
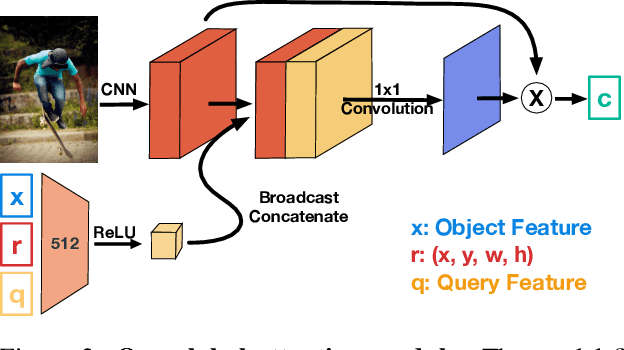
The problem of language grounding has attracted much attention in recent years due to its pivotal role in more general image-lingual high level reasoning tasks (e.g., image captioning, VQA). Despite the tremendous progress in visual grounding, the performance of most approaches has been hindered by the quality of bounding box proposals obtained in the early stages of all recent pipelines. To address this limitation, we propose a general progressive query-guided bounding box refinement architecture (OptiBox) that leverages global image encoding for added context. We apply this architecture in the context of the GroundeR model, first introduced in 2016, which has a number of unique and appealing properties, such as the ability to learn in the semi-supervised setting by leveraging cyclic language-reconstruction. Using GroundeR + OptiBox and a simple semantic language reconstruction loss that we propose, we achieve state-of-the-art grounding performance in the supervised setting on Flickr30k Entities dataset. More importantly, we are able to surpass many recent fully supervised models with only 50% of training data and perform competitively with as low as 3%.

Fast and Furious Convergence: Stochastic Second Order Methods under Interpolation

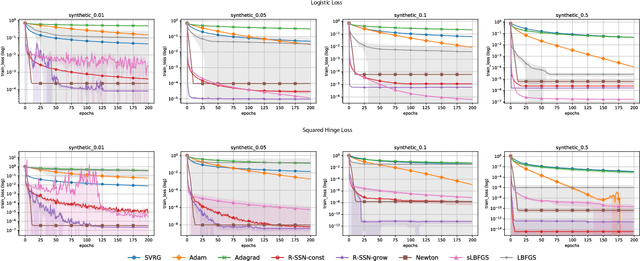
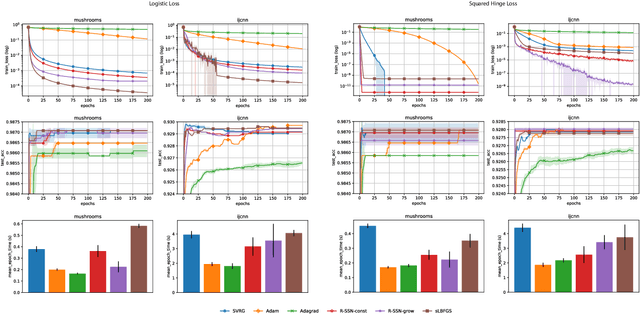
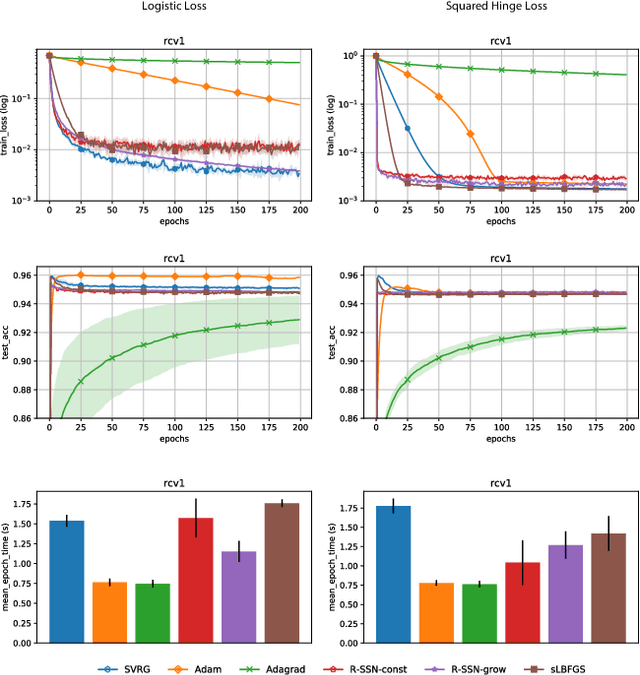
We consider stochastic second order methods for minimizing strongly-convex functions under an interpolation condition satisfied by over-parameterized models. Under this condition, we show that the regularized sub-sampled Newton method (R-SSN) achieves global linear convergence with an adaptive step size and a constant batch size. By growing the batch size for both the sub-sampled gradient and Hessian, we show that R-SSN can converge at a quadratic rate in a local neighbourhood of the solution. We also show that R-SSN attains local linear convergence for the family of self-concordant functions. Furthermore, we analyse stochastic BFGS algorithms in the interpolation setting and prove their global linear convergence. We empirically evaluate stochastic L-BFGS and a "Hessian-free" implementation of R-SSN for binary classification on synthetic, linearly-separable datasets and consider real medium-size datasets under a kernel mapping. Our experimental results show the fast convergence of these methods both in terms of the number of iterations and wall-clock time.