Adaptive Gradient Methods Converge Faster with Over-Parameterization (and you can do a line-search)
Paper and Code
Jun 11, 2020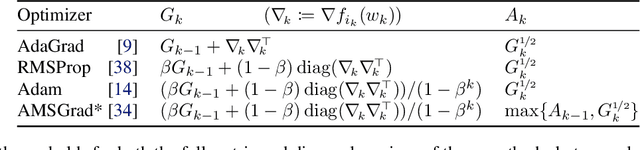
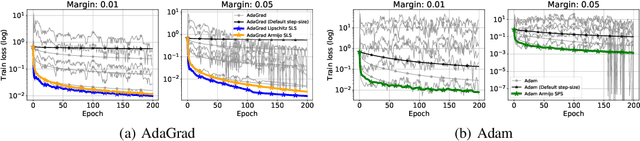

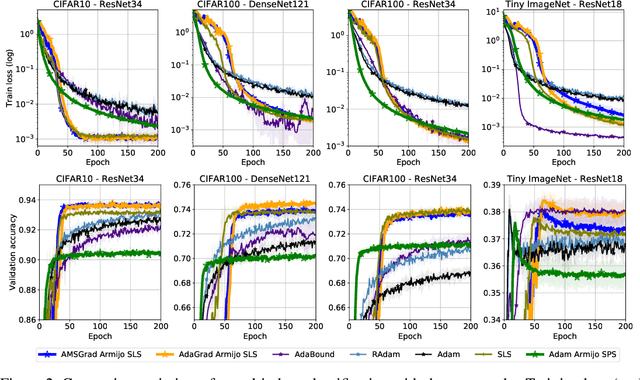
As adaptive gradient methods are typically used for training over-parameterized models capable of exactly fitting the data, we study their convergence in this interpolation setting. Under this assumption, we prove that constant step-size, zero-momentum variants of Adam and AMSGrad can converge to the minimizer at the O(1/T) rate for smooth, convex functions. When this assumption is only approximately satisfied, we show that these methods converge to a neighbourhood of the solution. On the other hand, we show that Adagrad is robust to the violation of interpolation and converges to the minimizer at the optimal rate. However, we demonstrate that even for simple, convex problems satisfying interpolation, the empirical performance of these methods heavily depends on the step-size and requires tuning. We alleviate this problem by making use of stochastic line-search methods (SLS) and Polyak's step-sizes (SPS) to help these methods adapt to the function's local smoothness. We prove that adaptive methods used in conjunction with these techniques do not require knowledge of problem-dependent constants and retain the convergence guarantees of their constant step-size counterparts. Experimentally, we show that using SLS or SPS consistently improves the convergence of adaptive methods across tasks; from binary classification with kernel mappings to classification with deep neural networks. Furthermore, our empirical results show that Adagrad equipped with SLS generalizes better than SGD.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge