Fast and Furious Convergence: Stochastic Second Order Methods under Interpolation
Paper and Code
Oct 11, 2019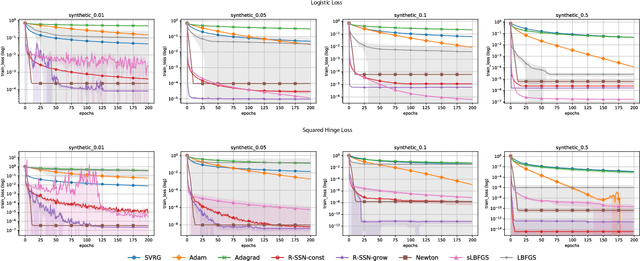
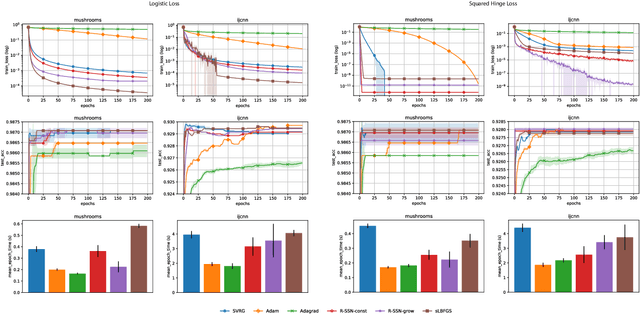
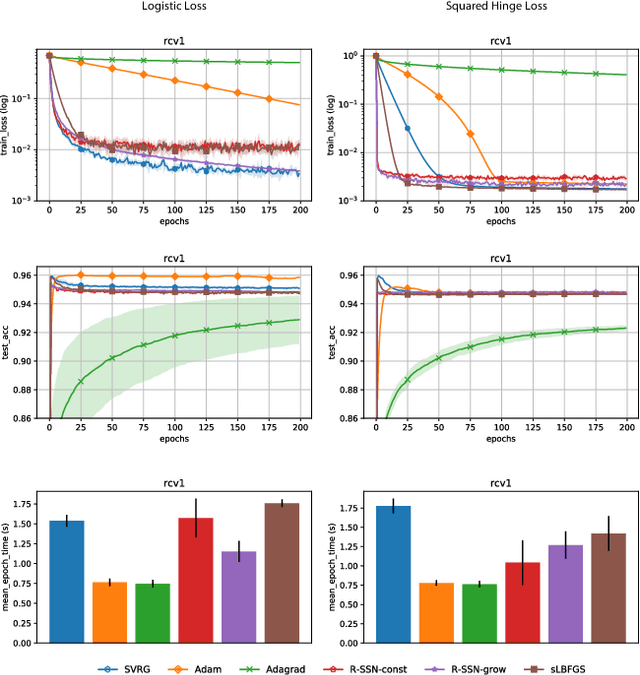
We consider stochastic second order methods for minimizing strongly-convex functions under an interpolation condition satisfied by over-parameterized models. Under this condition, we show that the regularized sub-sampled Newton method (R-SSN) achieves global linear convergence with an adaptive step size and a constant batch size. By growing the batch size for both the sub-sampled gradient and Hessian, we show that R-SSN can converge at a quadratic rate in a local neighbourhood of the solution. We also show that R-SSN attains local linear convergence for the family of self-concordant functions. Furthermore, we analyse stochastic BFGS algorithms in the interpolation setting and prove their global linear convergence. We empirically evaluate stochastic L-BFGS and a "Hessian-free" implementation of R-SSN for binary classification on synthetic, linearly-separable datasets and consider real medium-size datasets under a kernel mapping. Our experimental results show the fast convergence of these methods both in terms of the number of iterations and wall-clock time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge