Edge-aware Hard Clustering Graph Pooling for Brain Imaging Data

Graph Convolutional Networks (GCNs) can capture non-Euclidean spatial dependence between different brain regions, and the graph pooling operator in GCNs is key to enhancing the representation learning capability and acquiring abnormal brain maps. However, the majority of existing research designs graph pooling operators only from the perspective of nodes while disregarding the original edge features, in a way that not only confines graph pooling application scenarios, but also diminishes its ability to capture critical substructures. In this study, a clustering graph pooling method that first supports multidimensional edge features, called Edge-aware hard clustering graph pooling (EHCPool), is developed. EHCPool proposes the first 'Edge-to-node' score evaluation criterion based on edge features to assess node feature significance. To more effectively capture the critical subgraphs, a novel Iteration n-top strategy is further designed to adaptively learn sparse hard clustering assignments for graphs. Subsequently, an innovative N-E Aggregation strategy is presented to aggregate node and edge feature information in each independent subgraph. The proposed model was evaluated on multi-site brain imaging public datasets and yielded state-of-the-art performance. We believe this method is the first deep learning tool with the potential to probe different types of abnormal functional brain networks from data-driven perspective. Core code is at: https://github.com/swfen/EHCPool.

Temporal Dynamic Synchronous Functional Brain Network for Schizophrenia Diagnosis and Lateralization Analysis

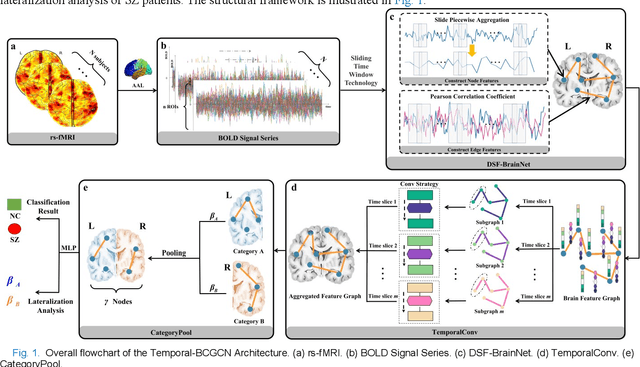
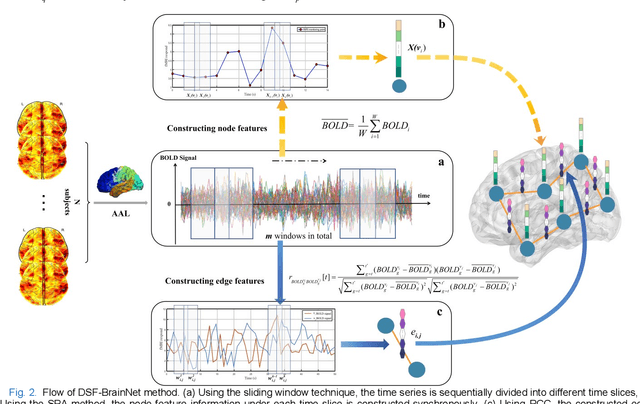
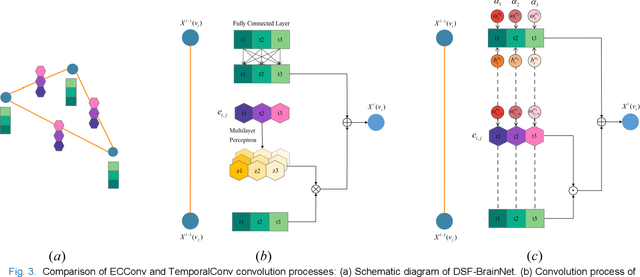
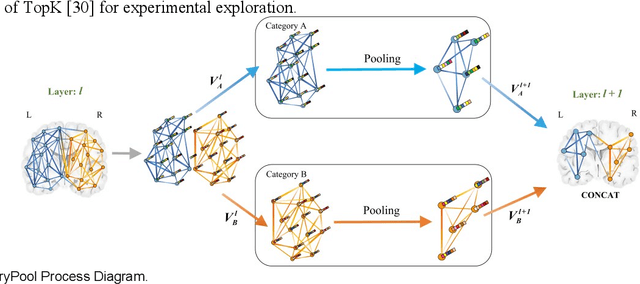
The available evidence suggests that dynamic functional connectivity (dFC) can capture time-varying abnormalities in brain activity in resting-state cerebral functional magnetic resonance imaging (rs-fMRI) data and has a natural advantage in uncovering mechanisms of abnormal brain activity in schizophrenia(SZ) patients. Hence, an advanced dynamic brain network analysis model called the temporal brain category graph convolutional network (Temporal-BCGCN) was employed. Firstly, a unique dynamic brain network analysis module, DSF-BrainNet, was designed to construct dynamic synchronization features. Subsequently, a revolutionary graph convolution method, TemporalConv, was proposed, based on the synchronous temporal properties of feature. Finally, the first modular abnormal hemispherical lateralization test tool in deep learning based on rs-fMRI data, named CategoryPool, was proposed. This study was validated on COBRE and UCLA datasets and achieved 83.62% and 89.71% average accuracies, respectively, outperforming the baseline model and other state-of-the-art methods. The ablation results also demonstrate the advantages of TemporalConv over the traditional edge feature graph convolution approach and the improvement of CategoryPool over the classical graph pooling approach. Interestingly, this study showed that the lower order perceptual system and higher order network regions in the left hemisphere are more severely dysfunctional than in the right hemisphere in SZ and reaffirms the importance of the left medial superior frontal gyrus in SZ. Our core code is available at: https://github.com/swfen/Temporal-BCGCN.

Nonseparable Symplectic Neural Networks

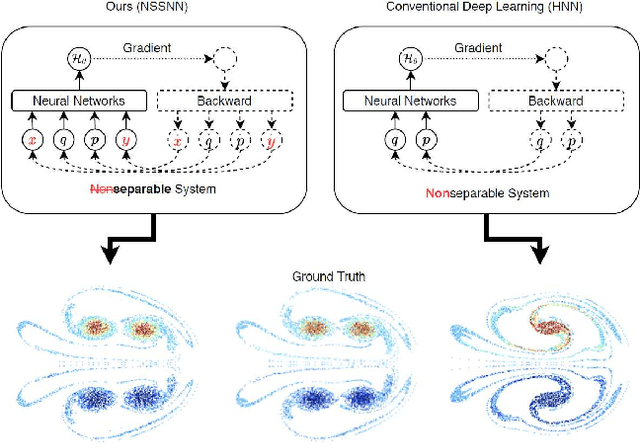
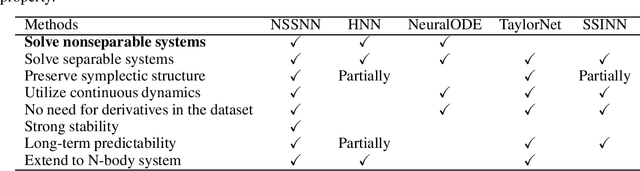
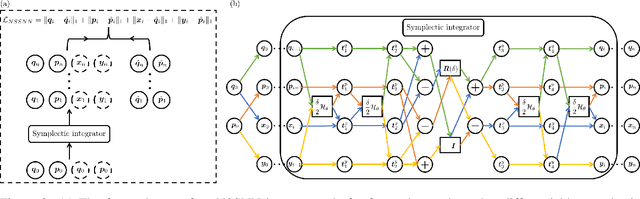
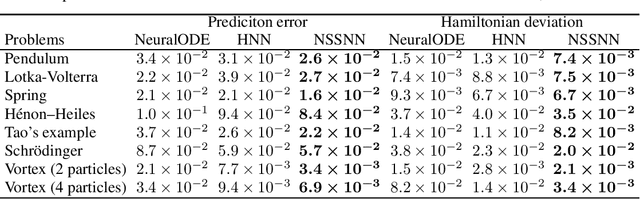
Predicting the behaviors of Hamiltonian systems has been drawing increasing attention in scientific machine learning. However, the vast majority of the literature was focused on predicting separable Hamiltonian systems with their kinematic and potential energy terms being explicitly decoupled, while building data-driven paradigms to predict nonseparable Hamiltonian systems that are ubiquitous in fluid dynamics and quantum mechanics were rarely explored. The main computational challenge lies in the effective embedding of symplectic priors to describe the inherently coupled evolution of position and momentum, which typically exhibits intricate dynamics with many degrees of freedom. To solve the problem, we propose a novel neural network architecture, Nonseparable Symplectic Neural Networks (NSSNNs), to uncover and embed the symplectic structure of a nonseparable Hamiltonian system from limited observation data. The enabling mechanics of our approach is an augmented symplectic time integrator to decouple the position and momentum energy terms and facilitate their evolution. We demonstrated the efficacy and versatility of our method by predicting a wide range of Hamiltonian systems, both separable and nonseparable, including vortical flow and quantum system. We showed the unique computational merits of our approach to yield long-term, accurate, and robust predictions for large-scale Hamiltonian systems by rigorously enforcing symplectomorphism.

Soft Multicopter Control using Neural Dynamics Identification

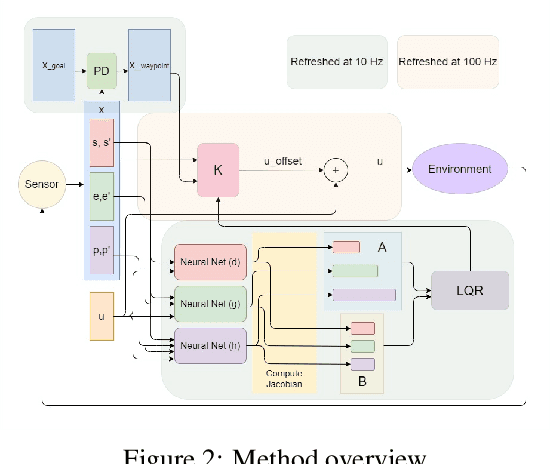
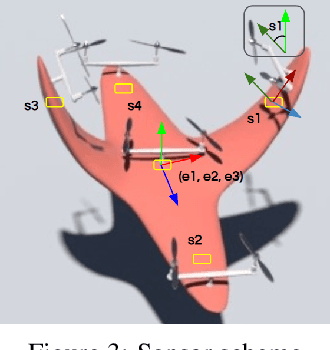
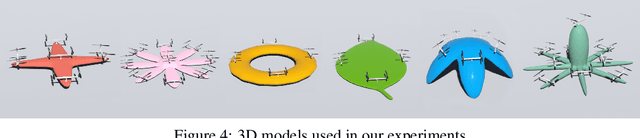
Dynamic control of a soft-body robot to deliver complex behaviors with low-dimensional actuation inputs is challenging. In this paper, we present a computational approach to automatically generate versatile, underactuated control policies that drives soft-bodied machines with complicated structures and nonlinear dynamics. Our target application is focused on the autonomous control of a soft multicopter, featured by its elastic material components, non-conventional shapes, and asymmetric rotor layouts, to precisely deliver compliant deformation and agile locomotion. The central piece of our approach lies in a lightweight neural surrogate model to identify and predict the temporal evolution of a set of geometric variables characterizing an elastic soft body. This physics-based learning model is further integrated into a Linear Quadratic Regulator (LQR) control loop enhanced by a novel online fixed-point relinearization scheme to accommodate the dynamic body balance, allowing an aggressive reduction of the computational overhead caused by the conventional full-scale sensing-simulation-control workflow. We demonstrate the efficacy of our approach by generating controllers for a broad spectrum of customized soft multicopter designs and testing them in a high-fidelity physics simulation environment. The control algorithm enables the multicopters to perform a variety of tasks, including hovering, trajectory tracking, cruising and active deforming.

Learning Physical Constraints with Neural Projections

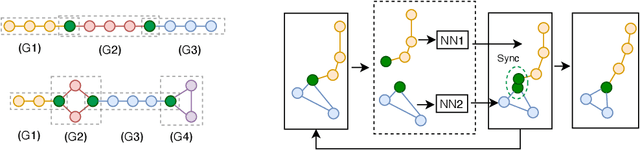
We propose a new family of neural networks to predict the behaviors of physical systems by learning their underpinning constraints. A neural projection operator liesat the heart of our approach, composed of a lightweight network with an embedded recursive architecture that interactively enforces learned underpinning constraints and predicts the various governed behaviors of different physical systems. Our neural projection operator is motivated by the position-based dynamics model that has been used widely in game and visual effects industries to unify the various fast physics simulators. Our method can automatically and effectively uncover a broad range of constraints from observation point data, such as length, angle, bending, collision, boundary effects, and their arbitrary combinations, without any connectivity priors. We provide a multi-group point representation in conjunction with a configurable network connection mechanism to incorporate prior inputs for processing complex physical systems. We demonstrated the efficacy of our approach by learning a set of challenging physical systems all in a unified and simple fashion including: rigid bodies with complex geometries, ropes with varying length and bending, articulated soft and rigid bodies, and multi-object collisions with complex boundaries.