Neural Partial Differential Equations with Functional Convolution

We present a lightweighted neural PDE representation to discover the hidden structure and predict the solution of different nonlinear PDEs. Our key idea is to leverage the prior of ``translational similarity'' of numerical PDE differential operators to drastically reduce the scale of learning model and training data. We implemented three central network components, including a neural functional convolution operator, a Picard forward iterative procedure, and an adjoint backward gradient calculator. Our novel paradigm fully leverages the multifaceted priors that stem from the sparse and smooth nature of the physical PDE solution manifold and the various mature numerical techniques such as adjoint solver, linearization, and iterative procedure to accelerate the computation. We demonstrate the efficacy of our method by robustly discovering the model and accurately predicting the solutions of various types of PDEs with small-scale networks and training sets. We highlight that all the PDE examples we showed were trained with up to 8 data samples and within 325 network parameters.

Nonseparable Symplectic Neural Networks

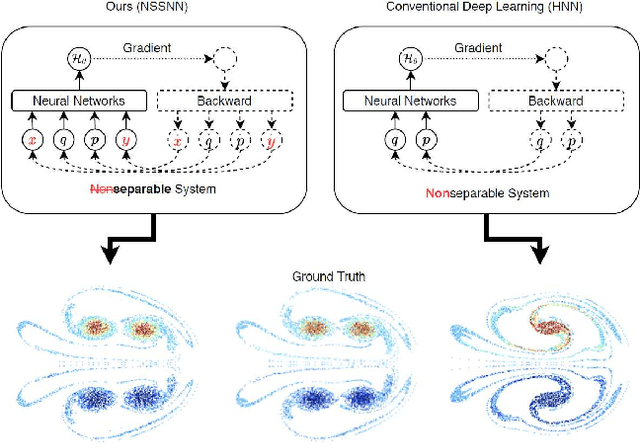
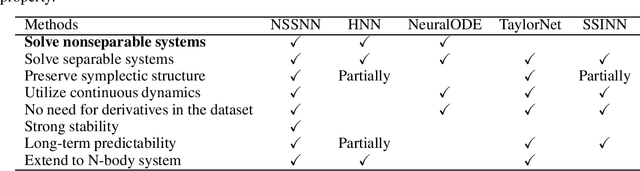
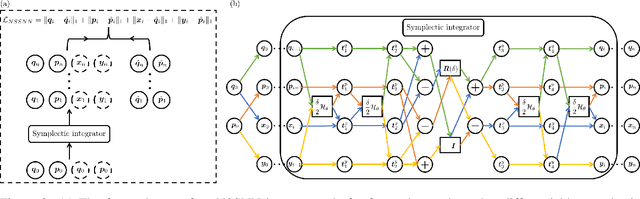
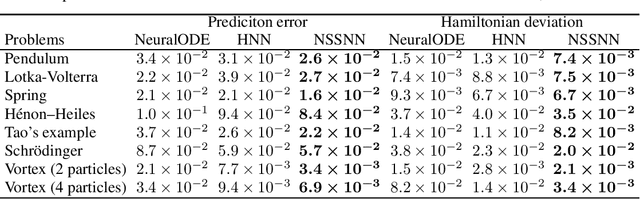
Predicting the behaviors of Hamiltonian systems has been drawing increasing attention in scientific machine learning. However, the vast majority of the literature was focused on predicting separable Hamiltonian systems with their kinematic and potential energy terms being explicitly decoupled, while building data-driven paradigms to predict nonseparable Hamiltonian systems that are ubiquitous in fluid dynamics and quantum mechanics were rarely explored. The main computational challenge lies in the effective embedding of symplectic priors to describe the inherently coupled evolution of position and momentum, which typically exhibits intricate dynamics with many degrees of freedom. To solve the problem, we propose a novel neural network architecture, Nonseparable Symplectic Neural Networks (NSSNNs), to uncover and embed the symplectic structure of a nonseparable Hamiltonian system from limited observation data. The enabling mechanics of our approach is an augmented symplectic time integrator to decouple the position and momentum energy terms and facilitate their evolution. We demonstrated the efficacy and versatility of our method by predicting a wide range of Hamiltonian systems, both separable and nonseparable, including vortical flow and quantum system. We showed the unique computational merits of our approach to yield long-term, accurate, and robust predictions for large-scale Hamiltonian systems by rigorously enforcing symplectomorphism.

Sparse Symplectically Integrated Neural Networks

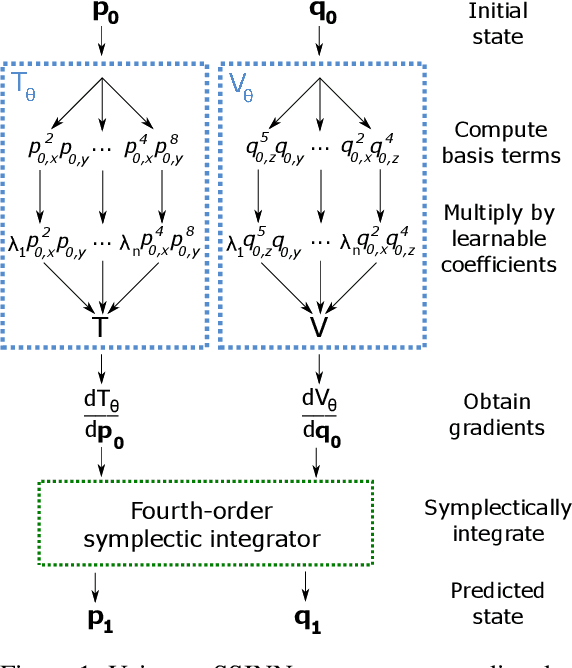
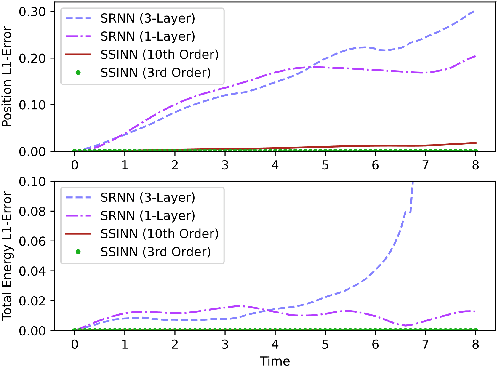
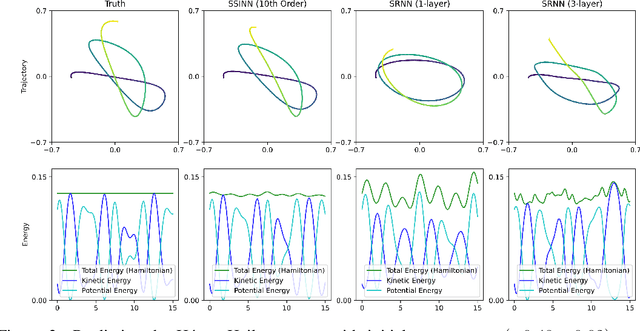
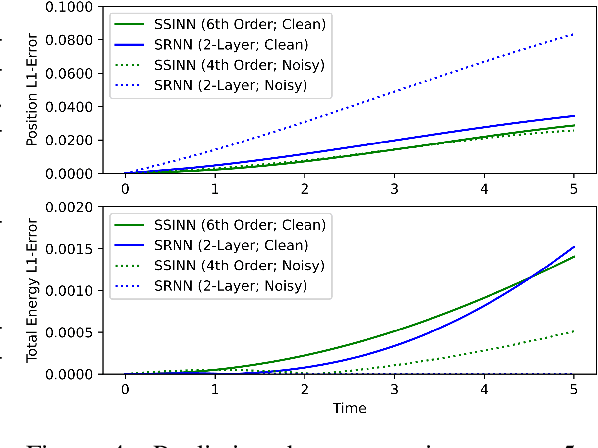
We introduce Sparse Symplectically Integrated Neural Networks (SSINNs), a novel model for learning Hamiltonian dynamical systems from data. SSINNs combine fourth-order symplectic integration with a learned parameterization of the Hamiltonian obtained using sparse regression through a mathematically elegant function space. This allows for interpretable models that incorporate symplectic inductive biases and have low memory requirements. We evaluate SSINNs on four classical Hamiltonian dynamical problems: the H\'enon-Heiles system, nonlinearly coupled oscillators, a multi-particle mass-spring system, and a pendulum system. Our results demonstrate promise in both system prediction and conservation of energy, outperforming the current state-of-the-art black-box prediction techniques by an order of magnitude. Further, SSINNs successfully converge to true governing equations from highly limited and noisy data, demonstrating potential applicability in the discovery of new physical governing equations.

RoeNets: Predicting Discontinuity of Hyperbolic Systems from Continuous Data

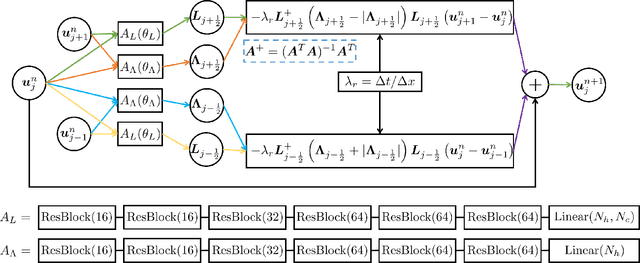
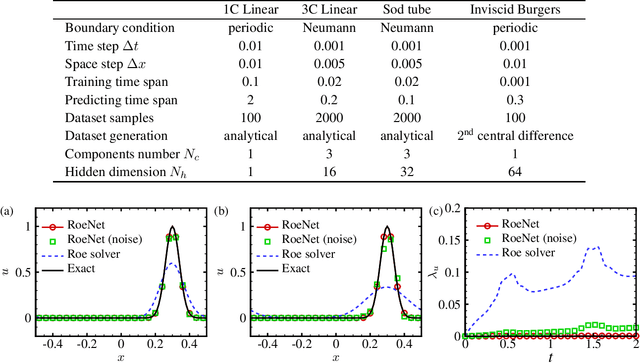
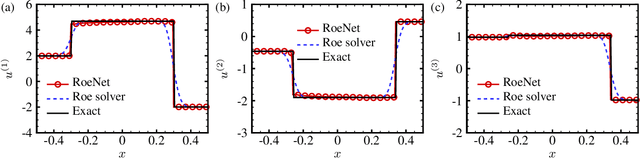
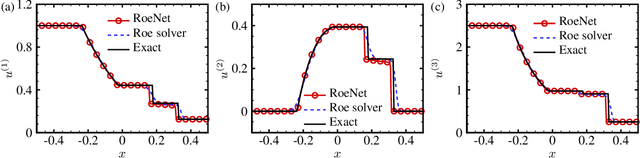
We introduce Roe Neural Networks (RoeNets) that can predict the discontinuity of the hyperbolic conservation laws (HCLs) based on short-term discontinuous and even continuous training data. Our methodology is inspired by Roe approximate Riemann solver (P. L. Roe, J. Comput. Phys., vol. 43, 1981, pp. 357--372), which is one of the most fundamental HCLs numerical solvers. In order to accurately solve the HCLs, Roe argues the need to construct a Roe matrix that fulfills "Property U", including diagonalizable with real eigenvalues, consistent with the exact Jacobian, and preserving conserved quantities. However, the construction of such matrix cannot be achieved by any general numerical method. Our model made a breakthrough improvement in solving the HCLs by applying Roe solver under a neural network perspective. To enhance the expressiveness of our model, we incorporate pseudoinverses into a novel context to enable a hidden dimension so that we are flexible with the number of parameters. The ability of our model to predict long-term discontinuity from a short window of continuous training data is in general considered impossible using traditional machine learning approaches. We demonstrate that our model can generate highly accurate predictions of evolution of convection without dissipation and the discontinuity of hyperbolic systems from smooth training data.

Neural Vortex Method: from Finite Lagrangian Particles to Infinite Dimensional Eulerian Dynamics

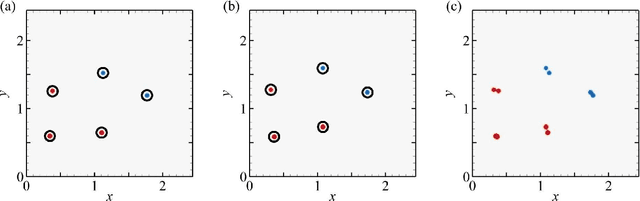
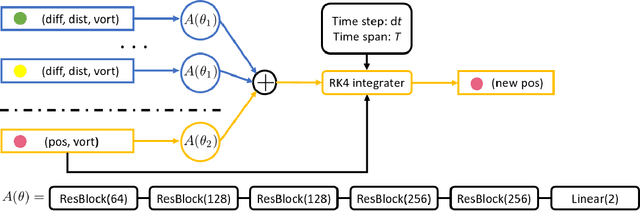
In the field of fluid numerical analysis, there has been a long-standing problem: lacking of a rigorous mathematical tool to map from a continuous flow field to discrete vortex particles, hurdling the Lagrangian particles from inheriting the high resolution of a large-scale Eulerian solver. To tackle this challenge, we propose a novel learning-based framework, the Neural Vortex Method (NVM), which builds a neural-network description of the Lagrangian vortex structures and their interaction dynamics to reconstruct the high-resolution Eulerian flow field in a physically-precise manner. The key components of our infrastructure consist of two networks: a vortex representation network to identify the Lagrangian vortices from a grid-based velocity field and a vortex interaction network to learn the underlying governing dynamics of these finite structures. By embedding these two networks with a vorticity-to-velocity Poisson solver and training its parameters using the high-fidelity data obtained from high-resolution direct numerical simulation, we can predict the accurate fluid dynamics on a precision level that was infeasible for all the previous conventional vortex methods (CVMs). To the best of our knowledge, our method is the first approach that can utilize motions of finite particles to learn infinite dimensional dynamic systems. We demonstrate the efficacy of our method in generating highly accurate prediction results, with low computational cost, of the leapfrogging vortex rings system, the turbulence system, and the systems governed by Euler equations with different external forces.

Symplectic Neural Networks in Taylor Series Form for Hamiltonian Systems

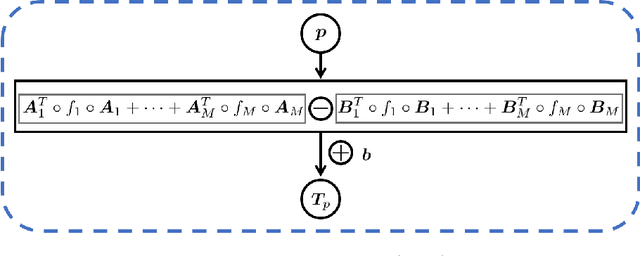
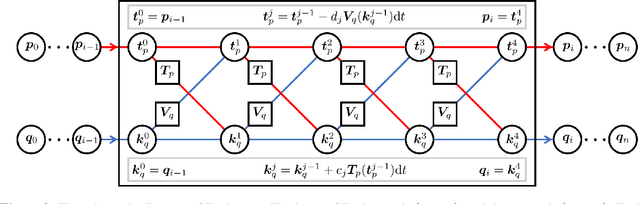
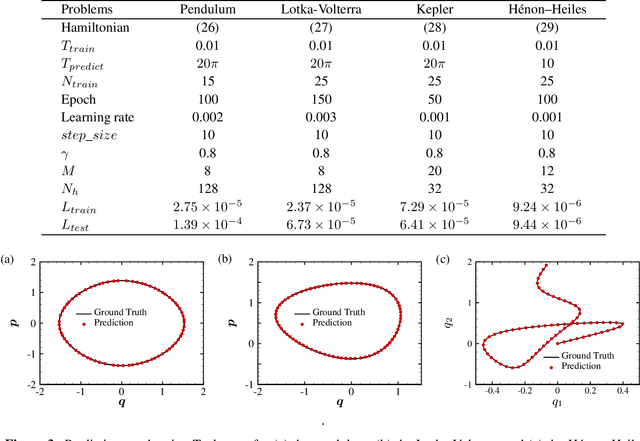
We propose an effective and light-weighted learning algorithm, Symplectic Taylor Neural Networks (Taylor-nets), to conduct continuous, long-term predictions of a complex Hamiltonian dynamic system based on sparse, short-term observations. At the heart of our algorithm is a novel neural network architecture consisting of two sub-networks. Both are embedded with terms in the form of Taylor series expansion that are designed with a symmetric structure. The key mechanism underpinning our infrastructure is the strong expressiveness and special symmetric property of the Taylor series expansion, which can inherently accommodate the numerical fitting process of the spatial derivatives of the Hamiltonian as well as preserve its symplectic structure. We further incorporate a fourth-order symplectic integrator in conjunction with neural ODEs' framework into our Taylor-net architecture to learn the continuous time evolution of the target systems while preserving their symplectic structures simultaneously. We demonstrated the efficacy of our Tayler-net in predicting a broad spectrum of Hamiltonian dynamic systems, including the pendulum, the Lotka-Volterra, the Kepler, and the H\`enon-Heiles systems. Compared with previous methods, our model exhibits its unique computational merits by using extremely small training data with short training period (6000 times shorter than the predicting period), small sample sizes (5 times smaller compared with the state-of-the-art methods), and no intermediary data to train the networks, while outperforming others to a great extent regarding the prediction accuracy, the convergence rate, and the robustness.