DiPietro-Hazari Kappa: A Novel Metric for Assessing Labeling Quality via Annotation

Data is a key component of modern machine learning, but statistics for assessing data label quality remain sparse in literature. Here, we introduce DiPietro-Hazari Kappa, a novel statistical metric for assessing the quality of suggested dataset labels in the context of human annotation. Rooted in the classical Fleiss's Kappa measure of inter-annotator agreement, the DiPietro-Hazari Kappa quantifies the the empirical annotator agreement differential that was attained above random chance. We offer a thorough theoretical examination of Fleiss's Kappa before turning to our derivation of DiPietro-Hazari Kappa. Finally, we conclude with a matrix formulation and set of procedural instructions for easy computational implementation.

Symplectically Integrated Symbolic Regression of Hamiltonian Dynamical Systems

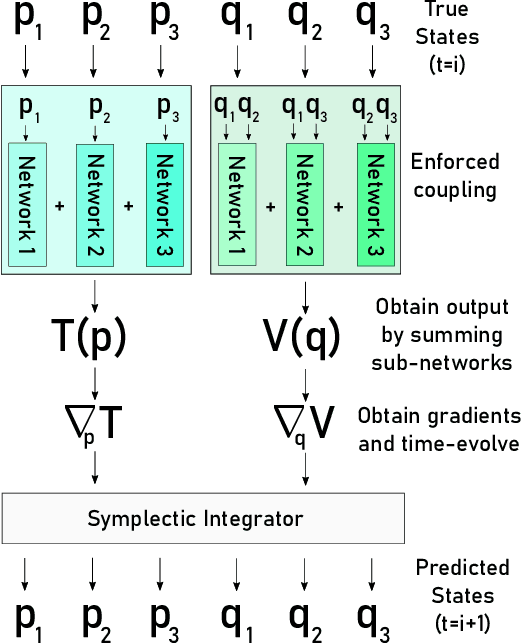
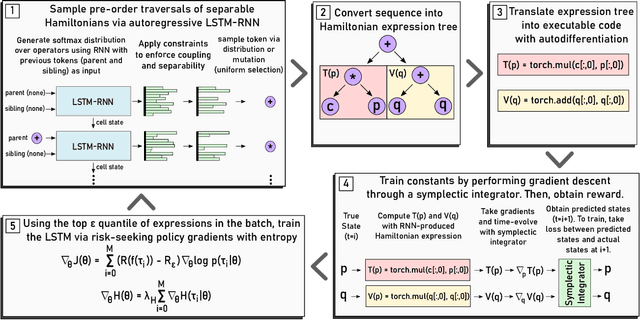
Here we present Symplectically Integrated Symbolic Regression (SISR), a novel technique for learning physical governing equations from data. SISR employs a deep symbolic regression approach, using a multi-layer LSTM-RNN with mutation to probabilistically sample Hamiltonian symbolic expressions. Using symplectic neural networks, we develop a model-agnostic approach for extracting meaningful physical priors from the data that can be imposed on-the-fly into the RNN output, limiting its search space. Hamiltonians generated by the RNN are optimized and assessed using a fourth-order symplectic integration scheme; prediction performance is used to train the LSTM-RNN to generate increasingly better functions via a risk-seeking policy gradients approach. Employing these techniques, we extract correct governing equations from oscillator, pendulum, two-body, and three-body gravitational systems with noisy and extremely small datasets.

Quantitative Stopword Generation for Sentiment Analysis via Recursive and Iterative Deletion

Stopwords carry little semantic information and are often removed from text data to reduce dataset size and improve machine learning model performance. Consequently, researchers have sought to develop techniques for generating effective stopword sets. Previous approaches have ranged from qualitative techniques relying upon linguistic experts, to statistical approaches that extract word importance using correlations or frequency-dependent metrics computed on a corpus. We present a novel quantitative approach that employs iterative and recursive feature deletion algorithms to see which words can be deleted from a pre-trained transformer's vocabulary with the least degradation to its performance, specifically for the task of sentiment analysis. Empirically, stopword lists generated via this approach drastically reduce dataset size while negligibly impacting model performance, in one such example shrinking the corpus by 28.4% while improving the accuracy of a trained logistic regression model by 0.25%. In another instance, the corpus was shrunk by 63.7% with a 2.8% decrease in accuracy. These promising results indicate that our approach can generate highly effective stopword sets for specific NLP tasks.

Sparse Symplectically Integrated Neural Networks

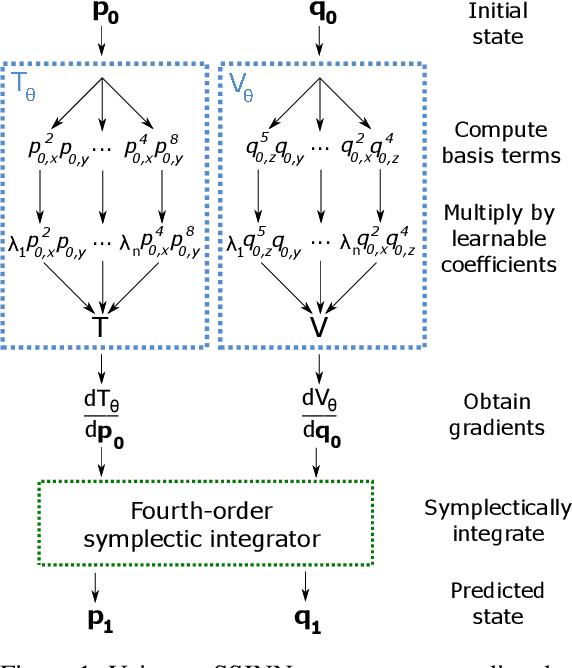
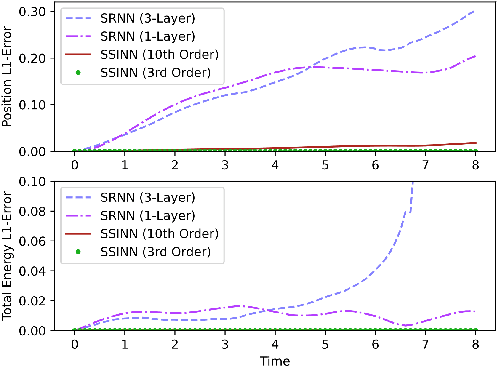
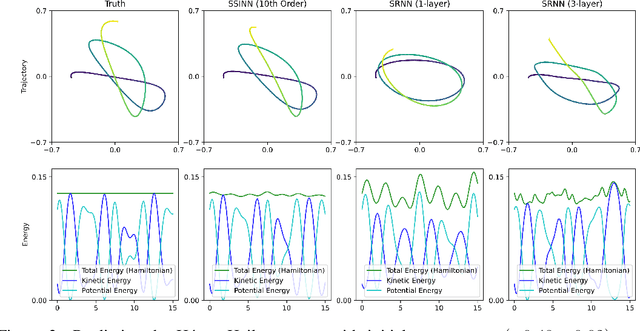
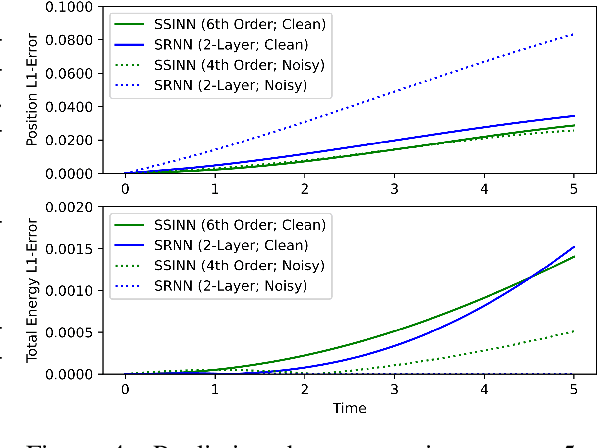
We introduce Sparse Symplectically Integrated Neural Networks (SSINNs), a novel model for learning Hamiltonian dynamical systems from data. SSINNs combine fourth-order symplectic integration with a learned parameterization of the Hamiltonian obtained using sparse regression through a mathematically elegant function space. This allows for interpretable models that incorporate symplectic inductive biases and have low memory requirements. We evaluate SSINNs on four classical Hamiltonian dynamical problems: the H\'enon-Heiles system, nonlinearly coupled oscillators, a multi-particle mass-spring system, and a pendulum system. Our results demonstrate promise in both system prediction and conservation of energy, outperforming the current state-of-the-art black-box prediction techniques by an order of magnitude. Further, SSINNs successfully converge to true governing equations from highly limited and noisy data, demonstrating potential applicability in the discovery of new physical governing equations.