Guanghan Pan
Symplectic Neural Networks in Taylor Series Form for Hamiltonian Systems
May 13, 2020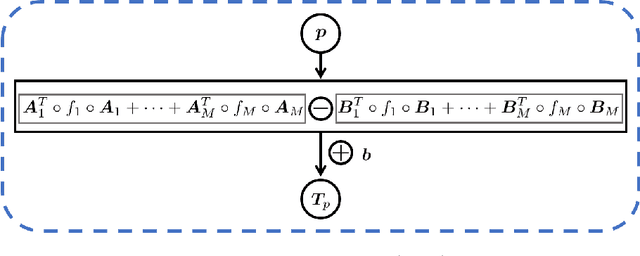
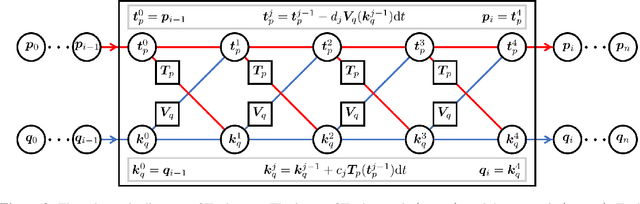

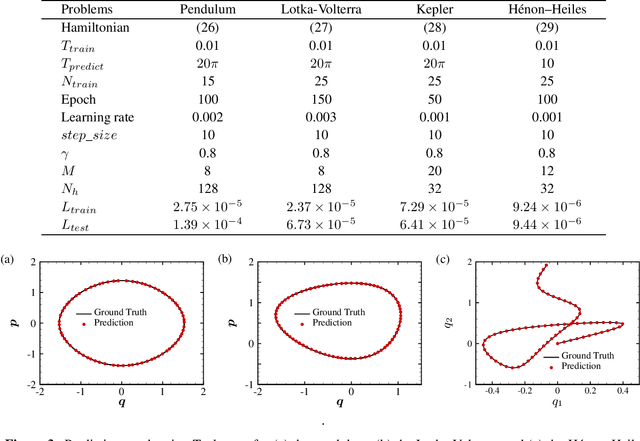
Abstract:We propose an effective and light-weighted learning algorithm, Symplectic Taylor Neural Networks (Taylor-nets), to conduct continuous, long-term predictions of a complex Hamiltonian dynamic system based on sparse, short-term observations. At the heart of our algorithm is a novel neural network architecture consisting of two sub-networks. Both are embedded with terms in the form of Taylor series expansion that are designed with a symmetric structure. The key mechanism underpinning our infrastructure is the strong expressiveness and special symmetric property of the Taylor series expansion, which can inherently accommodate the numerical fitting process of the spatial derivatives of the Hamiltonian as well as preserve its symplectic structure. We further incorporate a fourth-order symplectic integrator in conjunction with neural ODEs' framework into our Taylor-net architecture to learn the continuous time evolution of the target systems while preserving their symplectic structures simultaneously. We demonstrated the efficacy of our Tayler-net in predicting a broad spectrum of Hamiltonian dynamic systems, including the pendulum, the Lotka-Volterra, the Kepler, and the H\`enon-Heiles systems. Compared with previous methods, our model exhibits its unique computational merits by using extremely small training data with short training period (6000 times shorter than the predicting period), small sample sizes (5 times smaller compared with the state-of-the-art methods), and no intermediary data to train the networks, while outperforming others to a great extent regarding the prediction accuracy, the convergence rate, and the robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge