Mingrui Jing
Exploring Large Language Models in Healthcare: Insights into Corpora Sources, Customization Strategies, and Evaluation Metrics
Feb 17, 2025Abstract:This study reviewed the use of Large Language Models (LLMs) in healthcare, focusing on their training corpora, customization techniques, and evaluation metrics. A systematic search of studies from 2021 to 2024 identified 61 articles. Four types of corpora were used: clinical resources, literature, open-source datasets, and web-crawled data. Common construction techniques included pre-training, prompt engineering, and retrieval-augmented generation, with 44 studies combining multiple methods. Evaluation metrics were categorized into process, usability, and outcome metrics, with outcome metrics divided into model-based and expert-assessed outcomes. The study identified critical gaps in corpus fairness, which contributed to biases from geographic, cultural, and socio-economic factors. The reliance on unverified or unstructured data highlighted the need for better integration of evidence-based clinical guidelines. Future research should focus on developing a tiered corpus architecture with vetted sources and dynamic weighting, while ensuring model transparency. Additionally, the lack of standardized evaluation frameworks for domain-specific models called for comprehensive validation of LLMs in real-world healthcare settings.
Virtual Quantum Markov Chains
Dec 04, 2023Abstract:Quantum Markov chains generalize classical Markov chains for random variables to the quantum realm and exhibit unique inherent properties, making them an important feature in quantum information theory. In this work, we propose the concept of virtual quantum Markov chains (VQMCs), focusing on scenarios where subsystems retain classical information about global systems from measurement statistics. As a generalization of quantum Markov chains, VQMCs characterize states where arbitrary global shadow information can be recovered from subsystems through local quantum operations and measurements. We present an algebraic characterization for virtual quantum Markov chains and show that the virtual quantum recovery is fully determined by the block matrices of a quantum state on its subsystems. Notably, we find a distinction between two classes of tripartite entanglement by showing that the W state is a VQMC while the GHZ state is not. Furthermore, we establish semidefinite programs to determine the optimal sampling overhead and the robustness of virtual quantum Markov chains. We demonstrate the optimal sampling overhead is additive, indicating no free lunch to further reduce the sampling cost of recovery from parallel calls of the VQMC states. Our findings elucidate distinctions between quantum Markov chains and virtual quantum Markov chains, extending our understanding of quantum recovery to scenarios prioritizing classical information from measurement statistics.
Statistical Analysis of Quantum State Learning Process in Quantum Neural Networks
Sep 26, 2023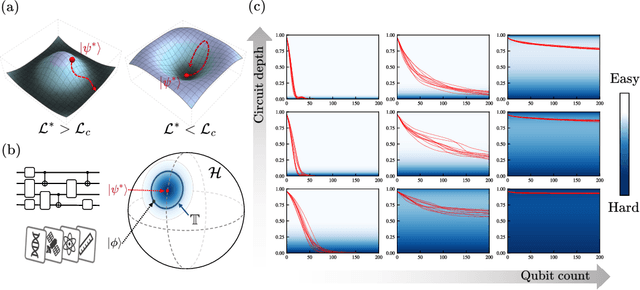
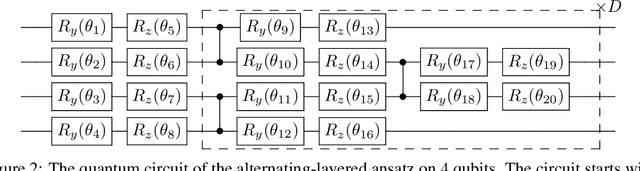
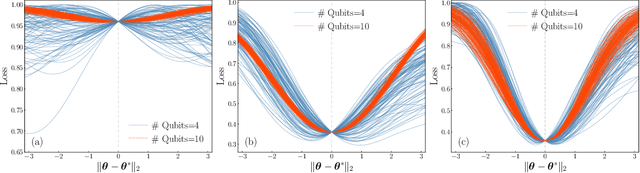
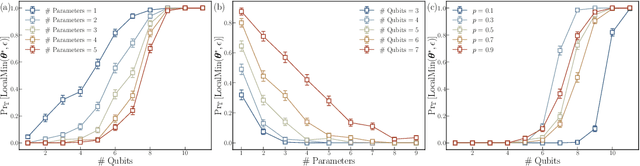
Abstract:Quantum neural networks (QNNs) have been a promising framework in pursuing near-term quantum advantage in various fields, where many applications can be viewed as learning a quantum state that encodes useful data. As a quantum analog of probability distribution learning, quantum state learning is theoretically and practically essential in quantum machine learning. In this paper, we develop a no-go theorem for learning an unknown quantum state with QNNs even starting from a high-fidelity initial state. We prove that when the loss value is lower than a critical threshold, the probability of avoiding local minima vanishes exponentially with the qubit count, while only grows polynomially with the circuit depth. The curvature of local minima is concentrated to the quantum Fisher information times a loss-dependent constant, which characterizes the sensibility of the output state with respect to parameters in QNNs. These results hold for any circuit structures, initialization strategies, and work for both fixed ansatzes and adaptive methods. Extensive numerical simulations are performed to validate our theoretical results. Our findings place generic limits on good initial guesses and adaptive methods for improving the learnability and scalability of QNNs, and deepen the understanding of prior information's role in QNNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge