Chenghong Zhu
Statistical Analysis of Quantum State Learning Process in Quantum Neural Networks
Sep 26, 2023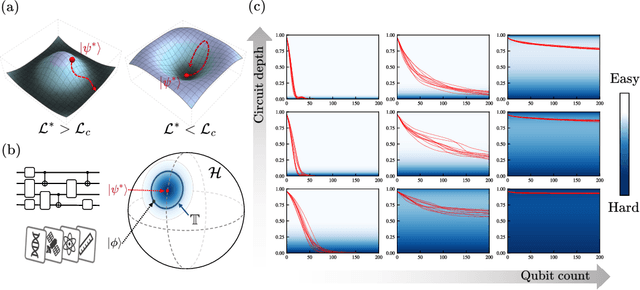
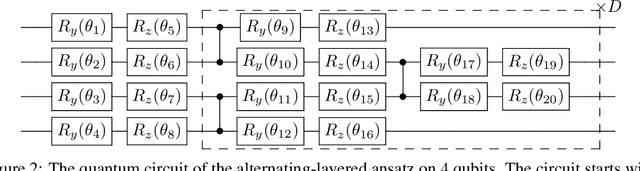
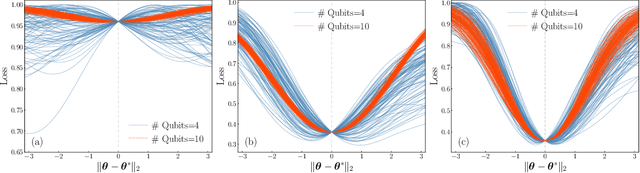
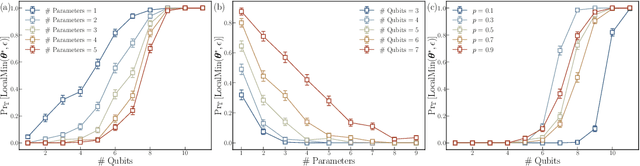
Abstract:Quantum neural networks (QNNs) have been a promising framework in pursuing near-term quantum advantage in various fields, where many applications can be viewed as learning a quantum state that encodes useful data. As a quantum analog of probability distribution learning, quantum state learning is theoretically and practically essential in quantum machine learning. In this paper, we develop a no-go theorem for learning an unknown quantum state with QNNs even starting from a high-fidelity initial state. We prove that when the loss value is lower than a critical threshold, the probability of avoiding local minima vanishes exponentially with the qubit count, while only grows polynomially with the circuit depth. The curvature of local minima is concentrated to the quantum Fisher information times a loss-dependent constant, which characterizes the sensibility of the output state with respect to parameters in QNNs. These results hold for any circuit structures, initialization strategies, and work for both fixed ansatzes and adaptive methods. Extensive numerical simulations are performed to validate our theoretical results. Our findings place generic limits on good initial guesses and adaptive methods for improving the learnability and scalability of QNNs, and deepen the understanding of prior information's role in QNNs.
Efficient information recovery from Pauli noise via classical shadow
May 06, 2023Abstract:The rapid advancement of quantum computing has led to an extensive demand for effective techniques to extract classical information from quantum systems, particularly in fields like quantum machine learning and quantum chemistry. However, quantum systems are inherently susceptible to noises, which adversely corrupt the information encoded in quantum systems. In this work, we introduce an efficient algorithm that can recover information from quantum states under Pauli noise. The core idea is to learn the necessary information of the unknown Pauli channel by post-processing the classical shadows of the channel. For a local and bounded-degree observable, only partial knowledge of the channel is required rather than its complete classical description to recover the ideal information, resulting in a polynomial-time algorithm. This contrasts with conventional methods such as probabilistic error cancellation, which requires the full information of the channel and exhibits exponential scaling with the number of qubits. We also prove that this scalable method is optimal on the sample complexity and generalise the algorithm to the weight contracting channel. Furthermore, we demonstrate the validity of the algorithm on the 1D anisotropic Heisenberg-type model via numerical simulations. As a notable application, our method can be severed as a sample-efficient error mitigation scheme for Clifford circuits.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge