Straightness of Rectified Flow: A Theoretical Insight into Wasserstein Convergence

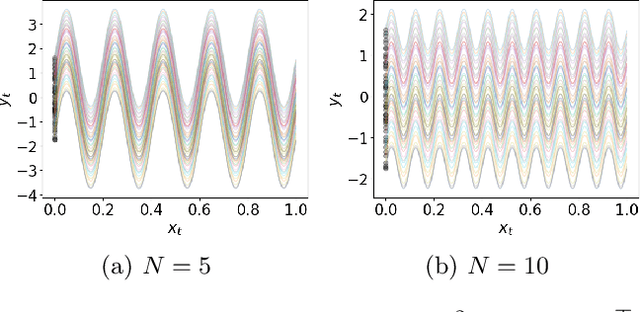
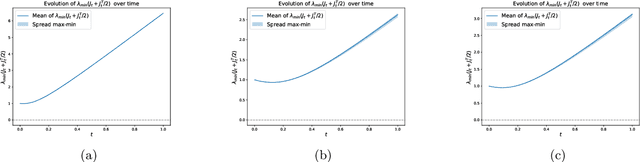
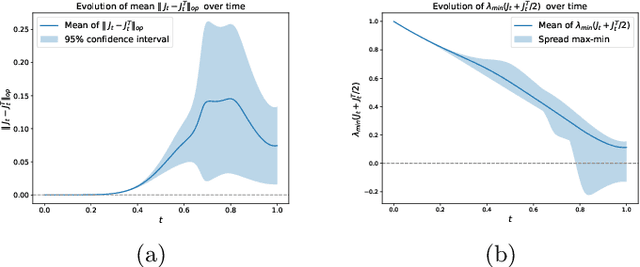
Diffusion models have emerged as a powerful tool for image generation and denoising. Typically, generative models learn a trajectory between the starting noise distribution and the target data distribution. Recently Liu et al. (2023b) designed a novel alternative generative model Rectified Flow (RF), which aims to learn straight flow trajectories from noise to data using a sequence of convex optimization problems with close ties to optimal transport. If the trajectory is curved, one must use many Euler discretization steps or novel strategies, such as exponential integrators, to achieve a satisfactory generation quality. In contrast, RF has been shown to theoretically straighten the trajectory through successive rectifications, reducing the number of function evaluations (NFEs) while sampling. It has also been shown empirically that RF may improve the straightness in two rectifications if one can solve the underlying optimization problem within a sufficiently small error. In this paper, we make two key theoretical contributions: 1) we provide the first theoretical analysis of the Wasserstein distance between the sampling distribution of RF and the target distribution. Our error rate is characterized by the number of discretization steps and a new formulation of straightness stronger than that in the original work. 2) In line with the previous empirical findings, we show that, for a rectified flow from a Gaussian to a mixture of two Gaussians, two rectifications are sufficient to achieve a straight flow. Additionally, we also present empirical results on both simulated and real datasets to validate our theoretical findings.

Feature Selection from Differentially Private Correlations

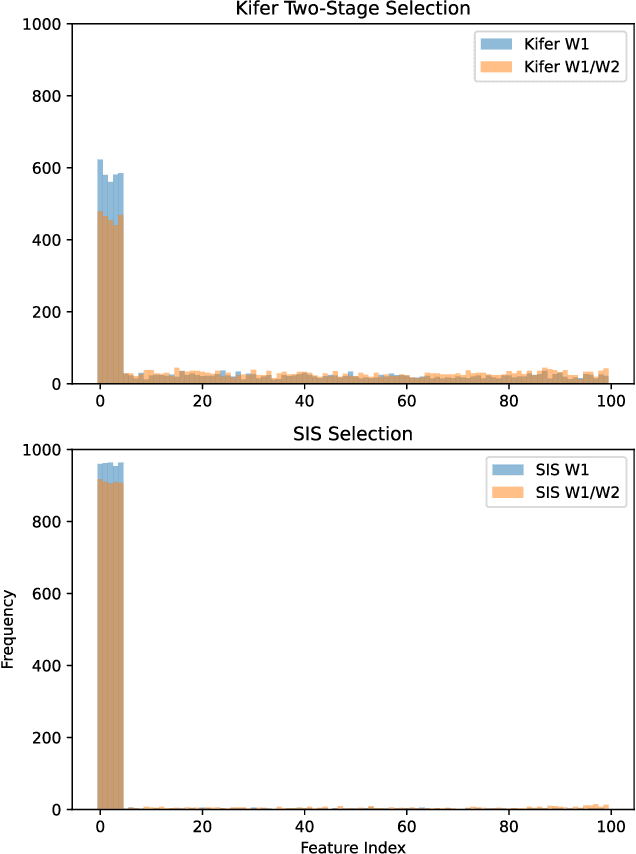
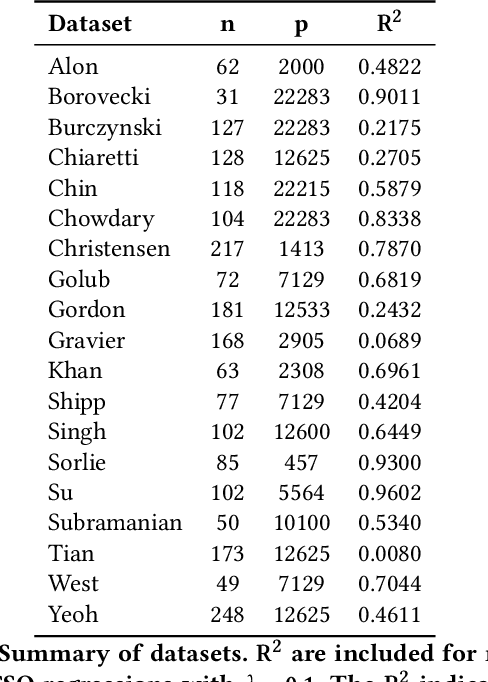
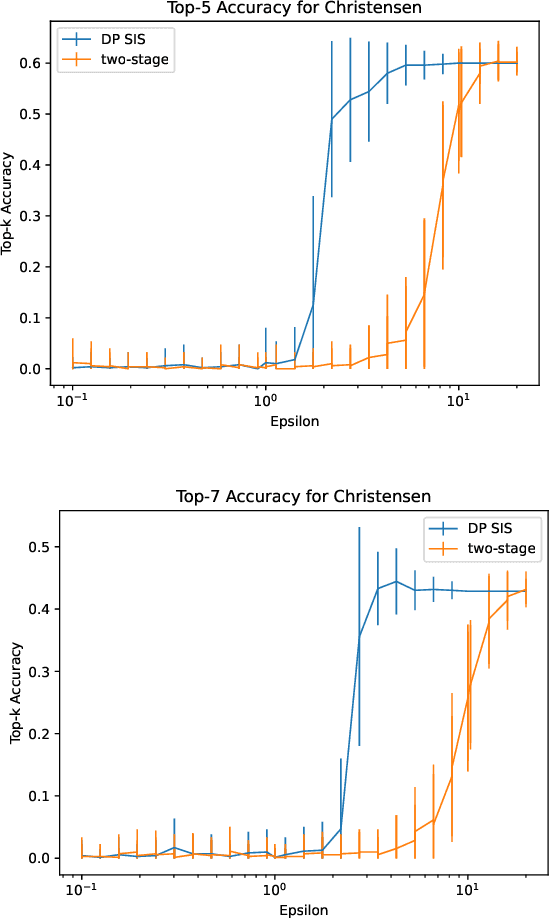
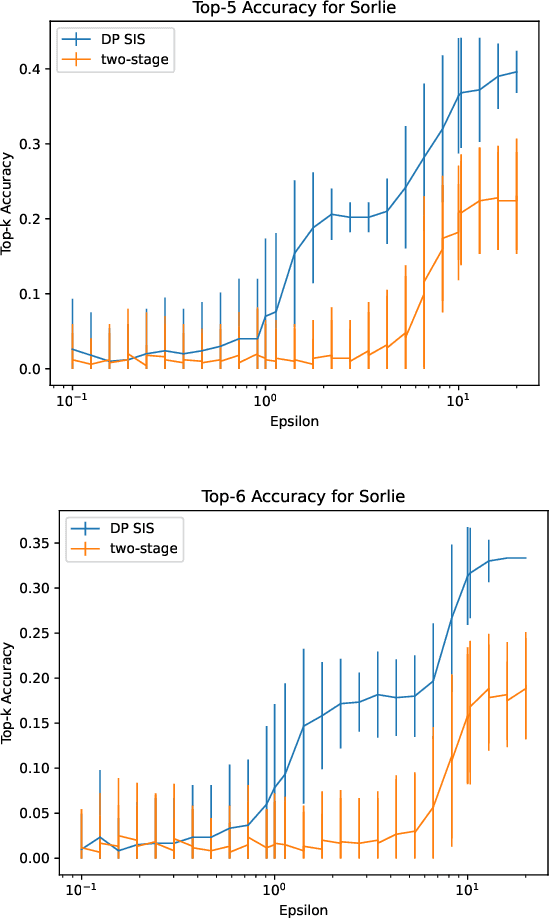
Data scientists often seek to identify the most important features in high-dimensional datasets. This can be done through $L_1$-regularized regression, but this can become inefficient for very high-dimensional datasets. Additionally, high-dimensional regression can leak information about individual datapoints in a dataset. In this paper, we empirically evaluate the established baseline method for feature selection with differential privacy, the two-stage selection technique, and show that it is not stable under sparsity. This makes it perform poorly on real-world datasets, so we consider a different approach to private feature selection. We employ a correlations-based order statistic to choose important features from a dataset and privatize them to ensure that the results do not leak information about individual datapoints. We find that our method significantly outperforms the established baseline for private feature selection on many datasets.

FLIPHAT: Joint Differential Privacy for High Dimensional Sparse Linear Bandits

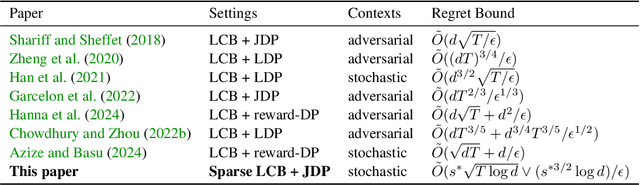
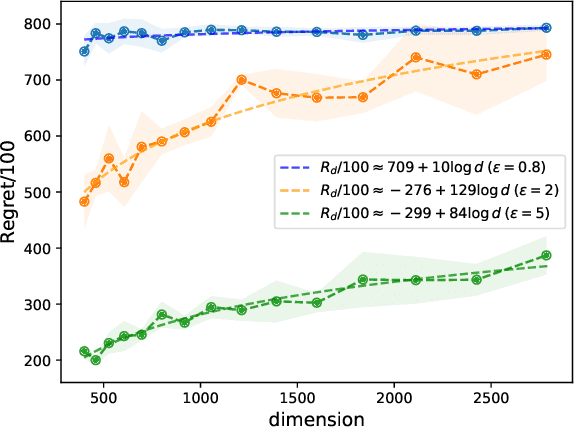
High dimensional sparse linear bandits serve as an efficient model for sequential decision-making problems (e.g. personalized medicine), where high dimensional features (e.g. genomic data) on the users are available, but only a small subset of them are relevant. Motivated by data privacy concerns in these applications, we study the joint differentially private high dimensional sparse linear bandits, where both rewards and contexts are considered as private data. First, to quantify the cost of privacy, we derive a lower bound on the regret achievable in this setting. To further address the problem, we design a computationally efficient bandit algorithm, \textbf{F}orgetfu\textbf{L} \textbf{I}terative \textbf{P}rivate \textbf{HA}rd \textbf{T}hresholding (FLIPHAT). Along with doubling of episodes and episodic forgetting, FLIPHAT deploys a variant of Noisy Iterative Hard Thresholding (N-IHT) algorithm as a sparse linear regression oracle to ensure both privacy and regret-optimality. We show that FLIPHAT achieves optimal regret up to logarithmic factors. We analyze the regret by providing a novel refined analysis of the estimation error of N-IHT, which is of parallel interest.

Directed Cyclic Graph for Causal Discovery from Multivariate Functional Data

Discovering causal relationship using multivariate functional data has received a significant amount of attention very recently. In this article, we introduce a functional linear structural equation model for causal structure learning when the underlying graph involving the multivariate functions may have cycles. To enhance interpretability, our model involves a low-dimensional causal embedded space such that all the relevant causal information in the multivariate functional data is preserved in this lower-dimensional subspace. We prove that the proposed model is causally identifiable under standard assumptions that are often made in the causal discovery literature. To carry out inference of our model, we develop a fully Bayesian framework with suitable prior specifications and uncertainty quantification through posterior summaries. We illustrate the superior performance of our method over existing methods in terms of causal graph estimation through extensive simulation studies. We also demonstrate the proposed method using a brain EEG dataset.

On the Computational Complexity of Private High-dimensional Model Selection via the Exponential Mechanism

We consider the problem of model selection in a high-dimensional sparse linear regression model under the differential privacy framework. In particular, we consider the problem of differentially private best subset selection and study its utility guarantee. We adopt the well-known exponential mechanism for selecting the best model, and under a certain margin condition, we establish its strong model recovery property. However, the exponential search space of the exponential mechanism poses a serious computational bottleneck. To overcome this challenge, we propose a Metropolis-Hastings algorithm for the sampling step and establish its polynomial mixing time to its stationary distribution in the problem parameters $n,p$, and $s$. Furthermore, we also establish approximate differential privacy for the final estimates of the Metropolis-Hastings random walk using its mixing property. Finally, we also perform some illustrative simulations that echo the theoretical findings of our main results.

Tale of two c(omplex)ities

For decades, best subset selection (BSS) has eluded statisticians mainly due to its computational bottleneck. However, until recently, modern computational breakthroughs have rekindled theoretical interest in BSS and have led to new findings. Recently, Guo et al. (2020) showed that the model selection performance of BSS is governed by a margin quantity that is robust to the design dependence, unlike modern methods such as LASSO, SCAD, MCP, etc. Motivated by their theoretical results, in this paper, we also study the variable selection properties of best subset selection for high-dimensional sparse linear regression setup. We show that apart from the identifiability margin, the following two complexity measures play a fundamental role in characterizing the margin condition for model consistency: (a) complexity of residualized features, (b) complexity of spurious projections. In particular, we establish a simple margin condition that only depends only on the identifiability margin quantity and the dominating one of the two complexity measures. Furthermore, we show that a similar margin condition depending on similar margin quantity and complexity measures is also necessary for model consistency of BSS. For a broader understanding of the complexity measures, we also consider some simple illustrative examples to demonstrate the variation in the complexity measures which broadens our theoretical understanding of the model selection performance of BSS under different correlation structures.

On Consistency and Asymptotic Normality of Least Absolute Deviation Estimators for 2-dimensional Sinusoidal Model

Estimation of the parameters of a 2-dimensional sinusoidal model is a fundamental problem in digital signal processing. In this paper, we propose a robust least absolute deviation (LAD) estimators for parameter estimation. The proposed methodology provides a robust alternative to non-robust estimation techniques like the least squares estimators, in situations where outliers are present in the data or in the presence of heavy tailed noise. We study important asymptotic properties of the LAD estimators and establish the strong consistency and asymptotic normality of the LAD estimators. We further illustrate the advantage of using LAD estimators over least squares estimators through extensive simulation studies.

Thompson Sampling for High-Dimensional Sparse Linear Contextual Bandits

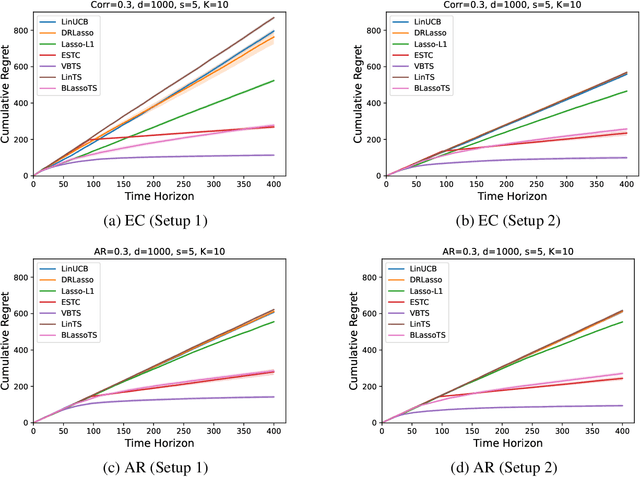
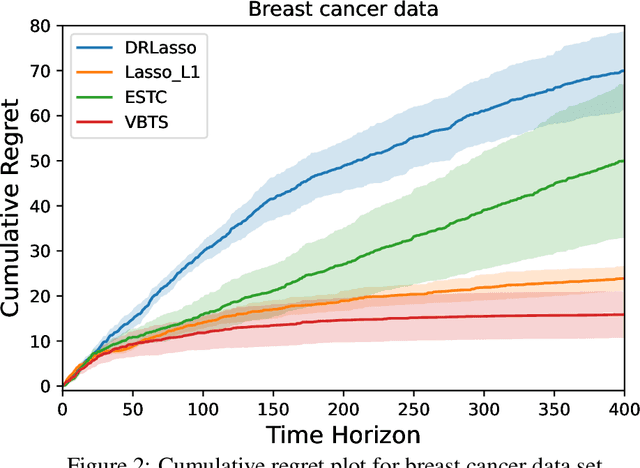
We consider the stochastic linear contextual bandit problem with high-dimensional features. We analyze the Thompson sampling (TS) algorithm, using special classes of sparsity-inducing priors (e.g. spike-and-slab) to model the unknown parameter, and provide a nearly optimal upper bound on the expected cumulative regret. To the best of our knowledge, this is the first work that provides theoretical guarantees of Thompson sampling in high dimensional and sparse contextual bandits. For faster computation, we use spike-and-slab prior to model the unknown parameter and variational inference instead of MCMC to approximate the posterior distribution. Extensive simulations demonstrate improved performance of our proposed algorithm over existing ones.

How does overparametrization affect performance on minority groups?

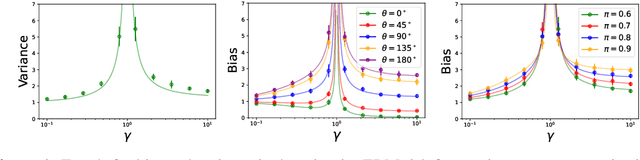
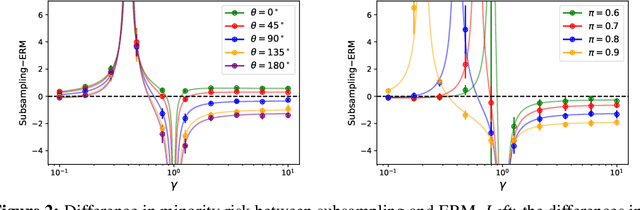
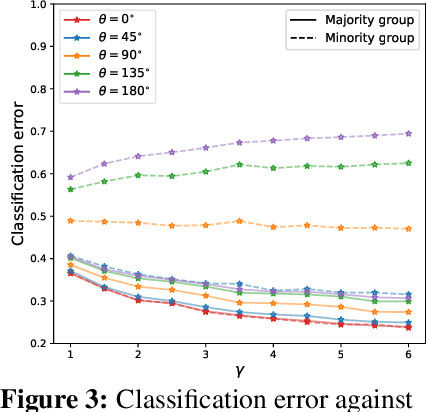
The benefits of overparameterization for the overall performance of modern machine learning (ML) models are well known. However, the effect of overparameterization at a more granular level of data subgroups is less understood. Recent empirical studies demonstrate encouraging results: (i) when groups are not known, overparameterized models trained with empirical risk minimization (ERM) perform better on minority groups; (ii) when groups are known, ERM on data subsampled to equalize group sizes yields state-of-the-art worst-group-accuracy in the overparameterized regime. In this paper, we complement these empirical studies with a theoretical investigation of the risk of overparameterized random feature models on minority groups. In a setting in which the regression functions for the majority and minority groups are different, we show that overparameterization always improves minority group performance.