FLIPHAT: Joint Differential Privacy for High Dimensional Sparse Linear Bandits

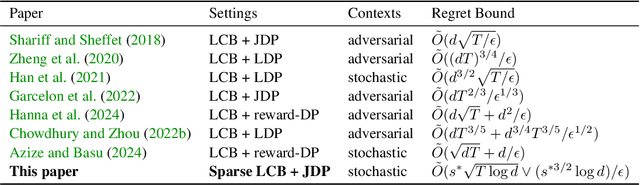
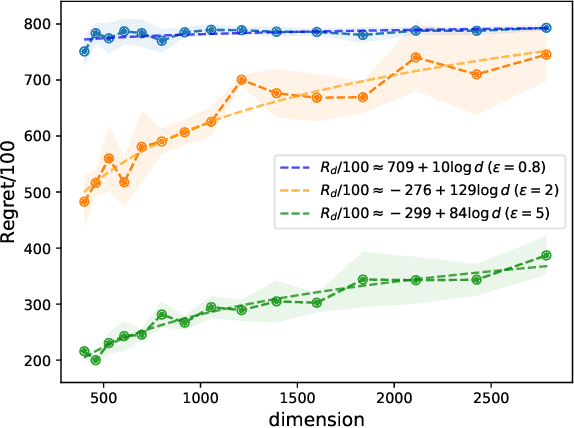
High dimensional sparse linear bandits serve as an efficient model for sequential decision-making problems (e.g. personalized medicine), where high dimensional features (e.g. genomic data) on the users are available, but only a small subset of them are relevant. Motivated by data privacy concerns in these applications, we study the joint differentially private high dimensional sparse linear bandits, where both rewards and contexts are considered as private data. First, to quantify the cost of privacy, we derive a lower bound on the regret achievable in this setting. To further address the problem, we design a computationally efficient bandit algorithm, \textbf{F}orgetfu\textbf{L} \textbf{I}terative \textbf{P}rivate \textbf{HA}rd \textbf{T}hresholding (FLIPHAT). Along with doubling of episodes and episodic forgetting, FLIPHAT deploys a variant of Noisy Iterative Hard Thresholding (N-IHT) algorithm as a sparse linear regression oracle to ensure both privacy and regret-optimality. We show that FLIPHAT achieves optimal regret up to logarithmic factors. We analyze the regret by providing a novel refined analysis of the estimation error of N-IHT, which is of parallel interest.

Thompson Sampling for High-Dimensional Sparse Linear Contextual Bandits

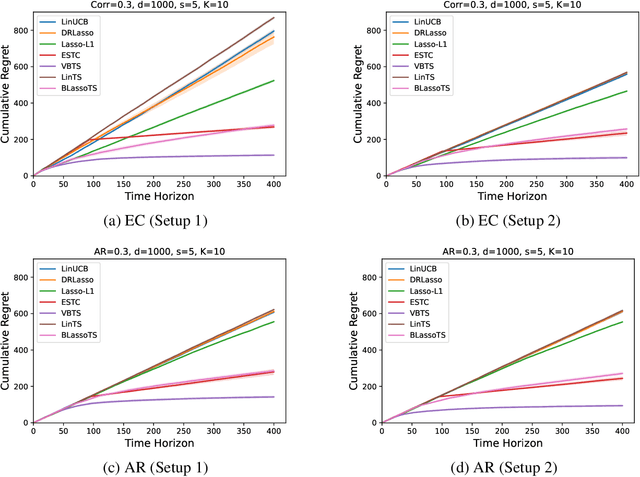
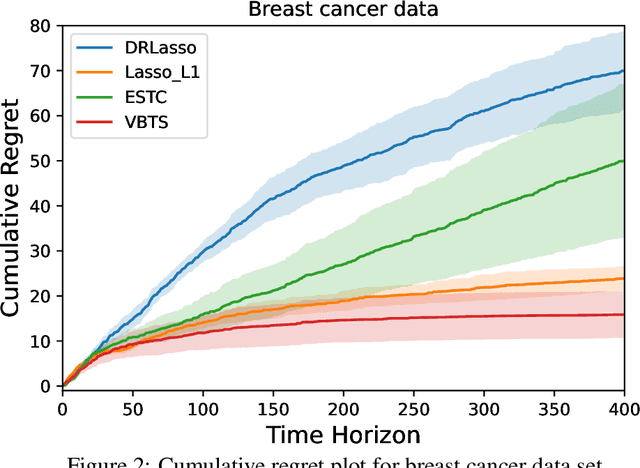
We consider the stochastic linear contextual bandit problem with high-dimensional features. We analyze the Thompson sampling (TS) algorithm, using special classes of sparsity-inducing priors (e.g. spike-and-slab) to model the unknown parameter, and provide a nearly optimal upper bound on the expected cumulative regret. To the best of our knowledge, this is the first work that provides theoretical guarantees of Thompson sampling in high dimensional and sparse contextual bandits. For faster computation, we use spike-and-slab prior to model the unknown parameter and variational inference instead of MCMC to approximate the posterior distribution. Extensive simulations demonstrate improved performance of our proposed algorithm over existing ones.

Scalable nonparametric Bayesian learning for heterogeneous and dynamic velocity fields

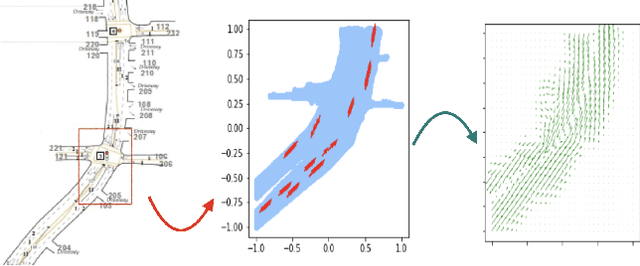
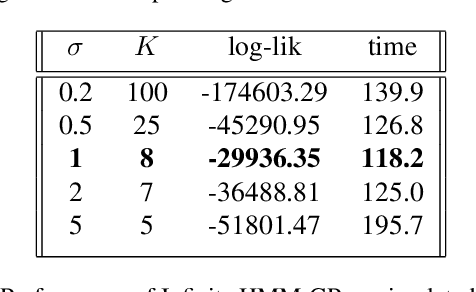
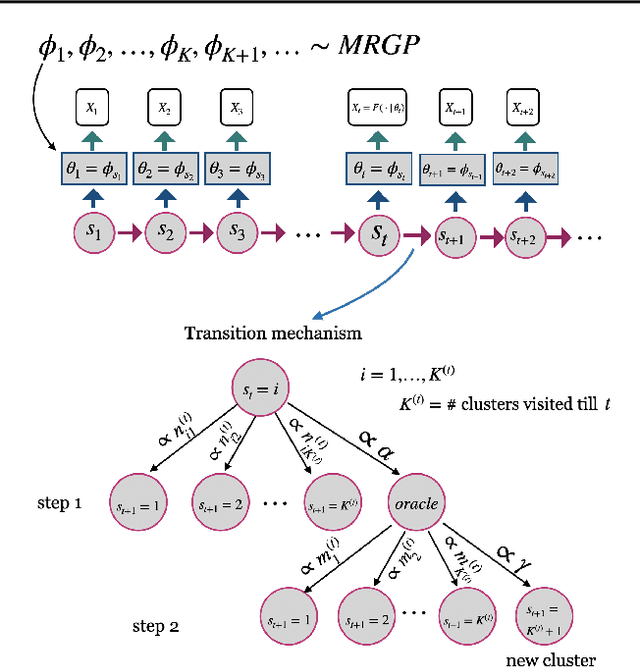
Analysis of heterogeneous patterns in complex spatio-temporal data finds usage across various domains in applied science and engineering, including training autonomous vehicles to navigate in complex traffic scenarios. Motivated by applications arising in the transportation domain, in this paper we develop a model for learning heterogeneous and dynamic patterns of velocity field data. We draw from basic nonparameric Bayesian modeling elements such as hierarchical Dirichlet process and infinite hidden Markov model, while the smoothness of each homogeneous velocity field element is captured with a Gaussian process prior. Of particular focus is a scalable approximate inference method for the proposed model; this is achieved by employing sequential MAP estimates from the infinite HMM model and an efficient sequential GP posterior computation technique, which is shown to work effectively on simulated data sets. Finally, we demonstrate the effectiveness of our techniques to the NGSIM dataset of complex multi-vehicle interactions.