Scalable nonparametric Bayesian learning for heterogeneous and dynamic velocity fields

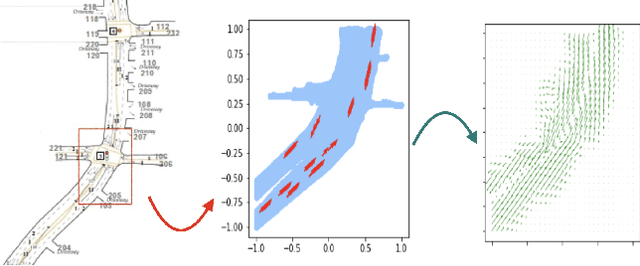
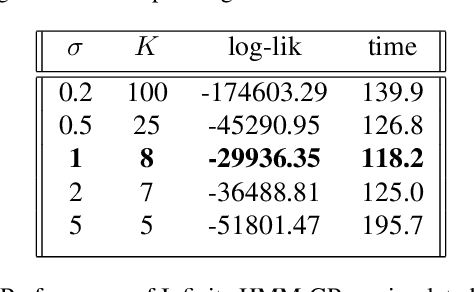
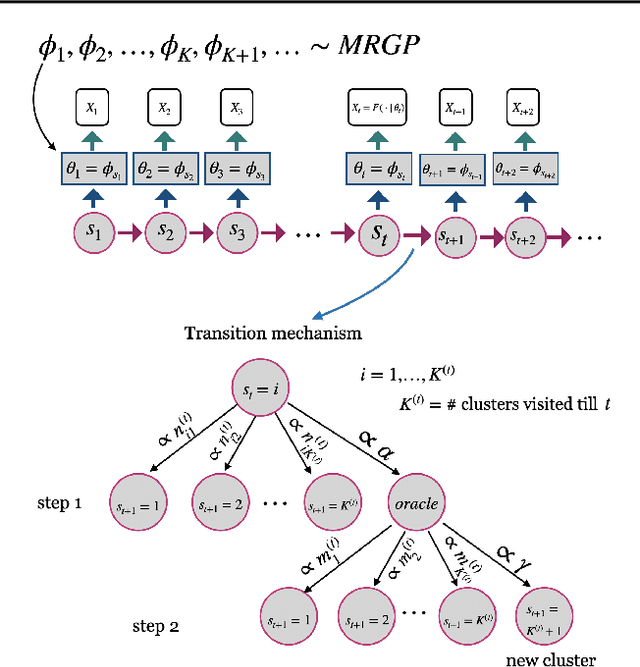
Analysis of heterogeneous patterns in complex spatio-temporal data finds usage across various domains in applied science and engineering, including training autonomous vehicles to navigate in complex traffic scenarios. Motivated by applications arising in the transportation domain, in this paper we develop a model for learning heterogeneous and dynamic patterns of velocity field data. We draw from basic nonparameric Bayesian modeling elements such as hierarchical Dirichlet process and infinite hidden Markov model, while the smoothness of each homogeneous velocity field element is captured with a Gaussian process prior. Of particular focus is a scalable approximate inference method for the proposed model; this is achieved by employing sequential MAP estimates from the infinite HMM model and an efficient sequential GP posterior computation technique, which is shown to work effectively on simulated data sets. Finally, we demonstrate the effectiveness of our techniques to the NGSIM dataset of complex multi-vehicle interactions.

Functional Optimal Transport: Mapping Estimation and Domain Adaptation for Functional data

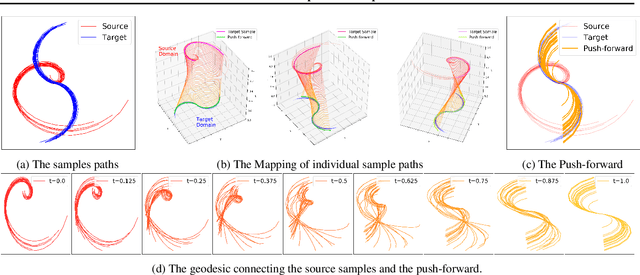
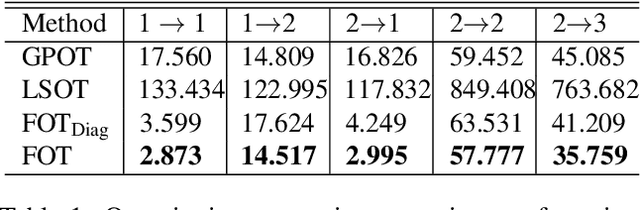
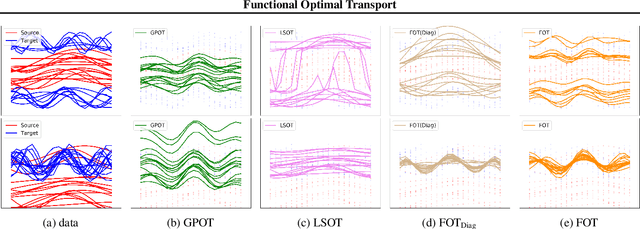
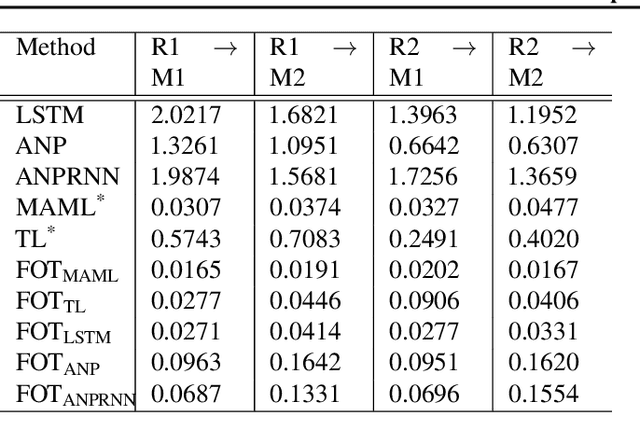
Optimal transport (OT) has generated much recent interest by its capability of finding mappings that transport mass from one distribution to another, and found useful roles in machine learning tasks such as unsupervised learning, domain adaptation and transfer learning. On the other hand, in many applications data are generated by complex mechanisms involving convoluted spaces of functions, curves and surfaces in high dimensions. Functional data analysis provides a useful framework of treatment for such domains. In this paper we introduce a novel formulation of optimal transport problem in functional spaces and develop an efficient learning algorithm for finding the stochastic map between functional domains. We apply our method to synthetic datasets and study the geometric properties of the transport map. Experiments on real-world datasets of robot arm trajectories and digit numbers further demonstrate the effectiveness of our method on applications of domain adaptation and generative modeling.

Robust Unsupervised Learning of Temporal Dynamic Interactions

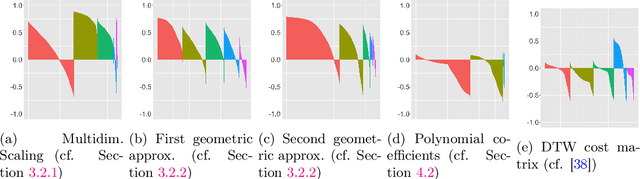
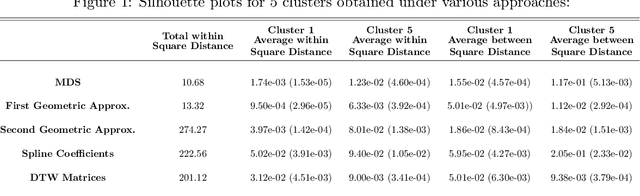
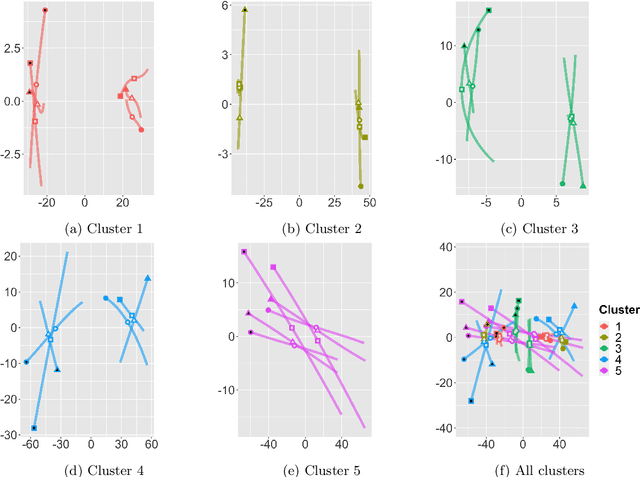
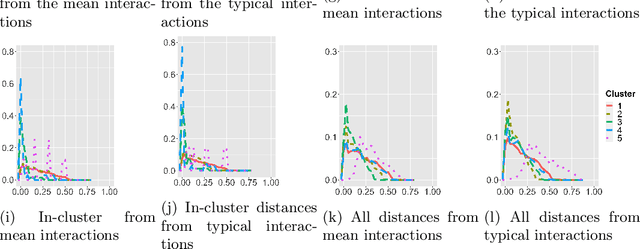
Robust representation learning of temporal dynamic interactions is an important problem in robotic learning in general and automated unsupervised learning in particular. Temporal dynamic interactions can be described by (multiple) geometric trajectories in a suitable space over which unsupervised learning techniques may be applied to extract useful features from raw and high-dimensional data measurements. Taking a geometric approach to robust representation learning for temporal dynamic interactions, it is necessary to develop suitable metrics and a systematic methodology for comparison and for assessing the stability of an unsupervised learning method with respect to its tuning parameters. Such metrics must account for the (geometric) constraints in the physical world as well as the uncertainty associated with the learned patterns. In this paper we introduce a model-free metric based on the Procrustes distance for robust representation learning of interactions, and an optimal transport based distance metric for comparing between distributions of interaction primitives. These distance metrics can serve as an objective for assessing the stability of an interaction learning algorithm. They are also used for comparing the outcomes produced by different algorithms. Moreover, they may also be adopted as an objective function to obtain clusters and representative interaction primitives. These concepts and techniques will be introduced, along with mathematical properties, while their usefulness will be demonstrated in unsupervised learning of vehicle-to-vechicle interactions extracted from the Safety Pilot database, the world's largest database for connected vehicles.