Interpolation for Robust Learning: Data Augmentation on Geodesics

We propose to study and promote the robustness of a model as per its performance through the interpolation of training data distributions. Specifically, (1) we augment the data by finding the worst-case Wasserstein barycenter on the geodesic connecting subpopulation distributions of different categories. (2) We regularize the model for smoother performance on the continuous geodesic path connecting subpopulation distributions. (3) Additionally, we provide a theoretical guarantee of robustness improvement and investigate how the geodesic location and the sample size contribute, respectively. Experimental validations of the proposed strategy on four datasets, including CIFAR-100 and ImageNet, establish the efficacy of our method, e.g., our method improves the baselines' certifiable robustness on CIFAR10 up to $7.7\%$, with $16.8\%$ on empirical robustness on CIFAR-100. Our work provides a new perspective of model robustness through the lens of Wasserstein geodesic-based interpolation with a practical off-the-shelf strategy that can be combined with existing robust training methods.

Towards Algorithmic Fairness in Space-Time: Filling in Black Holes

New technologies and the availability of geospatial data have drawn attention to spatio-temporal biases present in society. For example: the COVID-19 pandemic highlighted disparities in the availability of broadband service and its role in the digital divide; the environmental justice movement in the United States has raised awareness to health implications for minority populations stemming from historical redlining practices; and studies have found varying quality and coverage in the collection and sharing of open-source geospatial data. Despite the extensive literature on machine learning (ML) fairness, few algorithmic strategies have been proposed to mitigate such biases. In this paper we highlight the unique challenges for quantifying and addressing spatio-temporal biases, through the lens of use cases presented in the scientific literature and media. We envision a roadmap of ML strategies that need to be developed or adapted to quantify and overcome these challenges -- including transfer learning, active learning, and reinforcement learning techniques. Further, we discuss the potential role of ML in providing guidance to policy makers on issues related to spatial fairness.

Scalable nonparametric Bayesian learning for heterogeneous and dynamic velocity fields

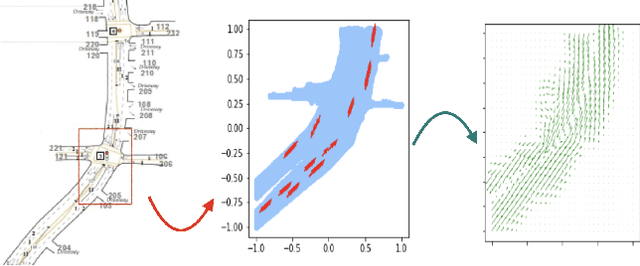
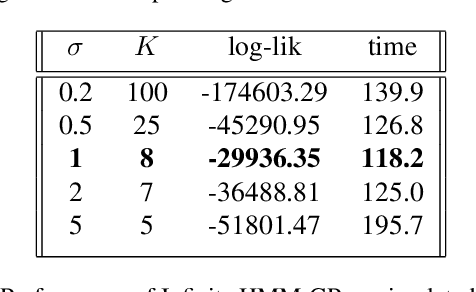
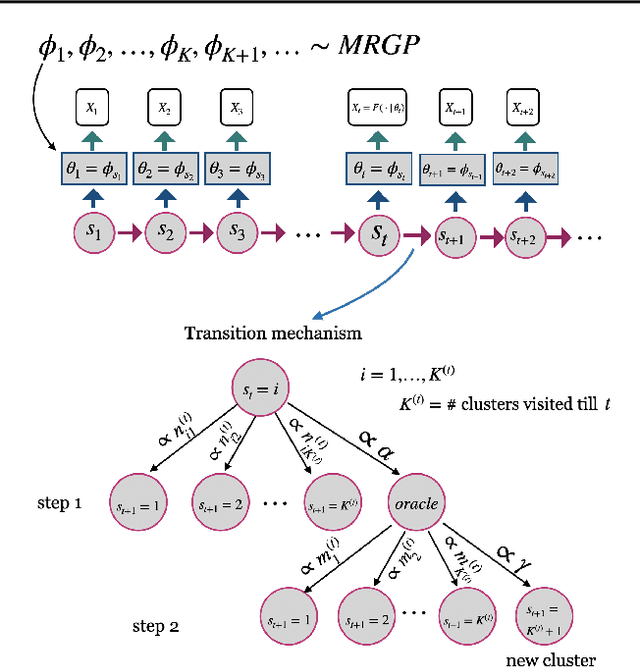
Analysis of heterogeneous patterns in complex spatio-temporal data finds usage across various domains in applied science and engineering, including training autonomous vehicles to navigate in complex traffic scenarios. Motivated by applications arising in the transportation domain, in this paper we develop a model for learning heterogeneous and dynamic patterns of velocity field data. We draw from basic nonparameric Bayesian modeling elements such as hierarchical Dirichlet process and infinite hidden Markov model, while the smoothness of each homogeneous velocity field element is captured with a Gaussian process prior. Of particular focus is a scalable approximate inference method for the proposed model; this is achieved by employing sequential MAP estimates from the infinite HMM model and an efficient sequential GP posterior computation technique, which is shown to work effectively on simulated data sets. Finally, we demonstrate the effectiveness of our techniques to the NGSIM dataset of complex multi-vehicle interactions.

Functional Optimal Transport: Mapping Estimation and Domain Adaptation for Functional data

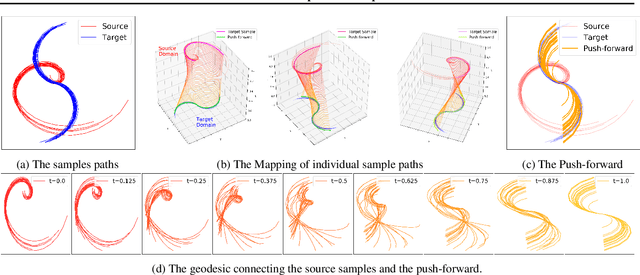
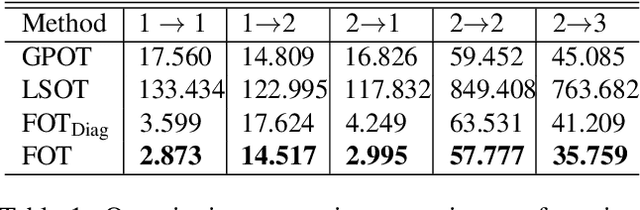
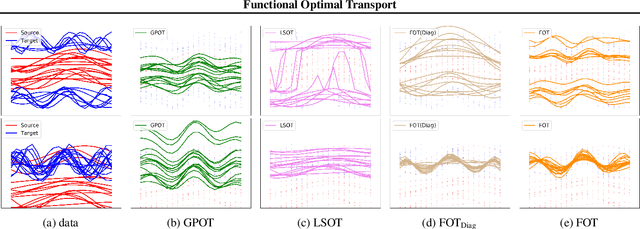
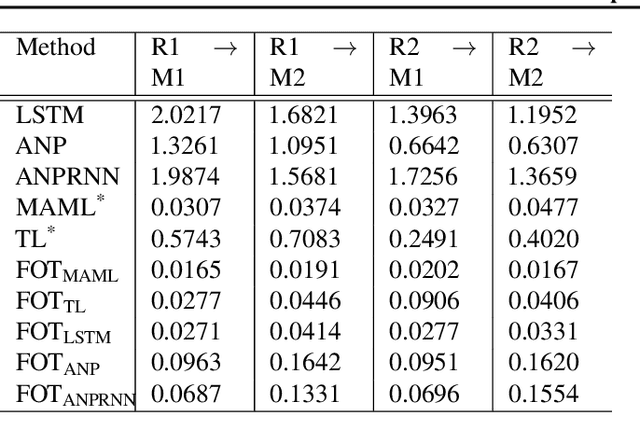
Optimal transport (OT) has generated much recent interest by its capability of finding mappings that transport mass from one distribution to another, and found useful roles in machine learning tasks such as unsupervised learning, domain adaptation and transfer learning. On the other hand, in many applications data are generated by complex mechanisms involving convoluted spaces of functions, curves and surfaces in high dimensions. Functional data analysis provides a useful framework of treatment for such domains. In this paper we introduce a novel formulation of optimal transport problem in functional spaces and develop an efficient learning algorithm for finding the stochastic map between functional domains. We apply our method to synthetic datasets and study the geometric properties of the transport map. Experiments on real-world datasets of robot arm trajectories and digit numbers further demonstrate the effectiveness of our method on applications of domain adaptation and generative modeling.

Robust Unsupervised Learning of Temporal Dynamic Interactions

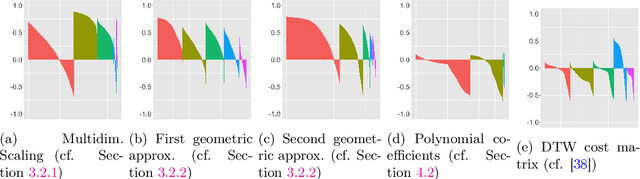
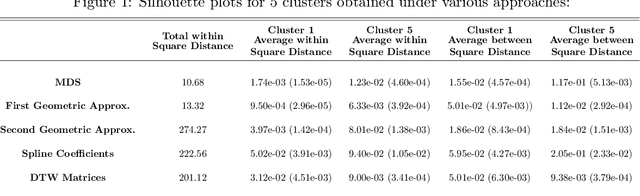
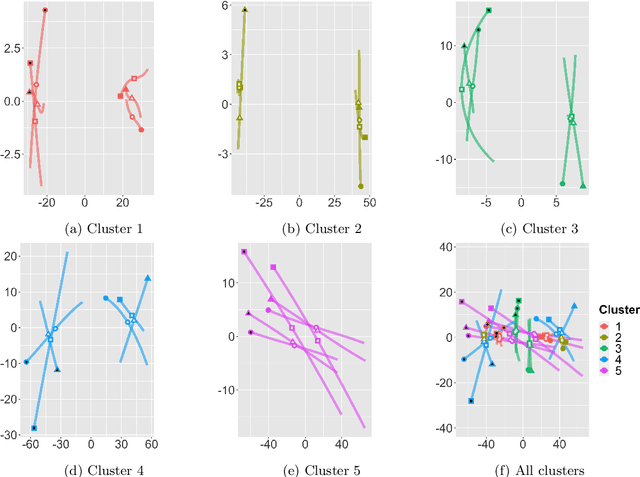
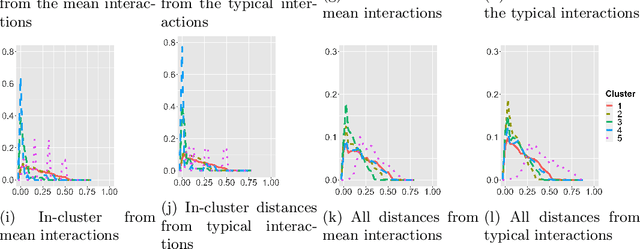
Robust representation learning of temporal dynamic interactions is an important problem in robotic learning in general and automated unsupervised learning in particular. Temporal dynamic interactions can be described by (multiple) geometric trajectories in a suitable space over which unsupervised learning techniques may be applied to extract useful features from raw and high-dimensional data measurements. Taking a geometric approach to robust representation learning for temporal dynamic interactions, it is necessary to develop suitable metrics and a systematic methodology for comparison and for assessing the stability of an unsupervised learning method with respect to its tuning parameters. Such metrics must account for the (geometric) constraints in the physical world as well as the uncertainty associated with the learned patterns. In this paper we introduce a model-free metric based on the Procrustes distance for robust representation learning of interactions, and an optimal transport based distance metric for comparing between distributions of interaction primitives. These distance metrics can serve as an objective for assessing the stability of an interaction learning algorithm. They are also used for comparing the outcomes produced by different algorithms. Moreover, they may also be adopted as an objective function to obtain clusters and representative interaction primitives. These concepts and techniques will be introduced, along with mathematical properties, while their usefulness will be demonstrated in unsupervised learning of vehicle-to-vechicle interactions extracted from the Safety Pilot database, the world's largest database for connected vehicles.

Dirichlet Simplex Nest and Geometric Inference

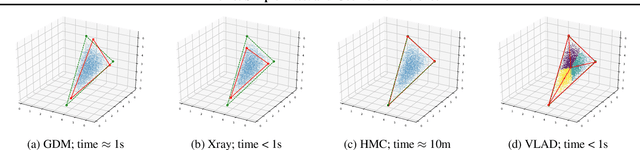
We propose Dirichlet Simplex Nest, a class of probabilistic models suitable for a variety of data types, and develop fast and provably accurate inference algorithms by accounting for the model's convex geometry and low dimensional simplicial structure. By exploiting the connection to Voronoi tessellation and properties of Dirichlet distribution, the proposed inference algorithm is shown to achieve consistency and strong error bound guarantees on a range of model settings and data distributions. The effectiveness of our model and the learning algorithm is demonstrated by simulations and by analyses of text and financial data.

Streaming dynamic and distributed inference of latent geometric structures

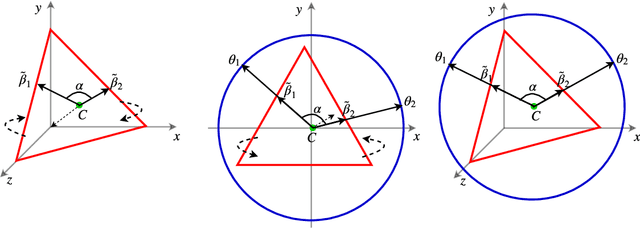
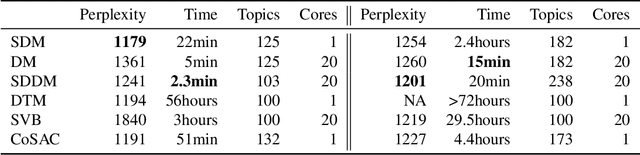
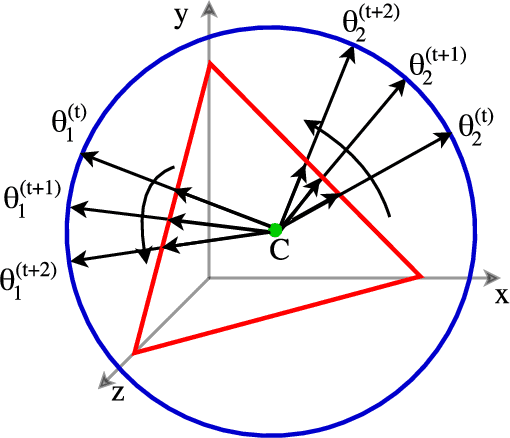
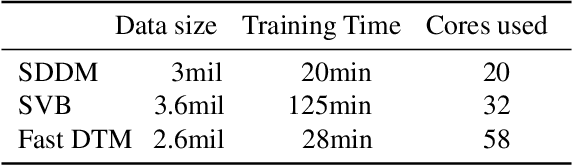
We develop new models and algorithms for learning the temporal dynamics of the topic polytopes and related geometric objects that arise in topic model based inference. Our model is nonparametric Bayesian and the corresponding inference algorithm is able to discover new topics as the time progresses. By exploiting the connection between the modeling of topic polytope evolution, Beta-Bernoulli process and the Hungarian matching algorithm, our method is shown to be several orders of magnitude faster than existing topic modeling approaches, as demonstrated by experiments working with several million documents in a dozen minutes.

Conic Scan-and-Cover algorithms for nonparametric topic modeling

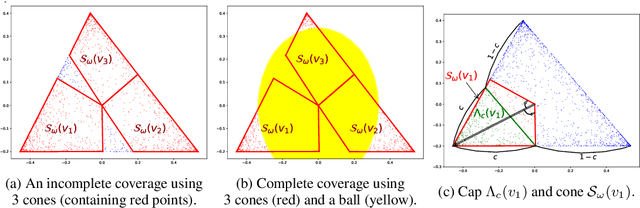
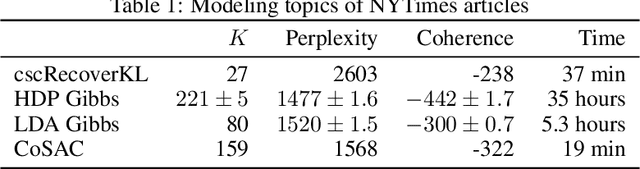
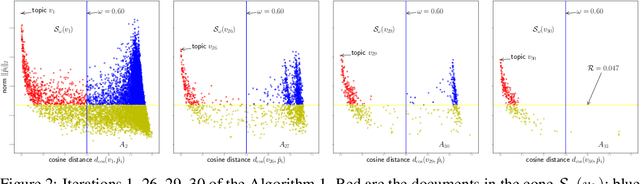
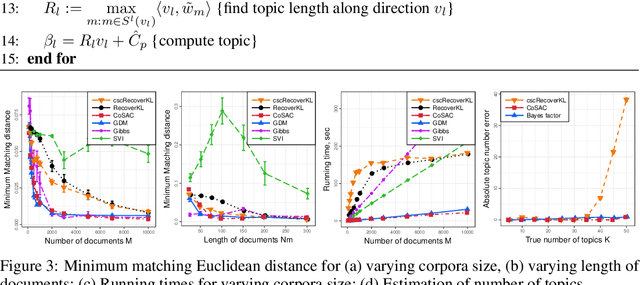
We propose new algorithms for topic modeling when the number of topics is unknown. Our approach relies on an analysis of the concentration of mass and angular geometry of the topic simplex, a convex polytope constructed by taking the convex hull of vertices representing the latent topics. Our algorithms are shown in practice to have accuracy comparable to a Gibbs sampler in terms of topic estimation, which requires the number of topics be given. Moreover, they are one of the fastest among several state of the art parametric techniques. Statistical consistency of our estimator is established under some conditions.