Certifiable Robustness for Naive Bayes Classifiers

Data cleaning is crucial but often laborious in most machine learning (ML) applications. However, task-agnostic data cleaning is sometimes unnecessary if certain inconsistencies in the dirty data will not affect the prediction of ML models to the test points. A test point is certifiably robust for an ML classifier if the prediction remains the same regardless of which (among exponentially many) cleaned dataset it is trained on. In this paper, we study certifiable robustness for the Naive Bayes classifier (NBC) on dirty datasets with missing values. We present (i) a linear time algorithm in the number of entries in the dataset that decides whether a test point is certifiably robust for NBC, (ii) an algorithm that counts for each label, the number of cleaned datasets on which the NBC can be trained to predict that label, and (iii) an efficient optimal algorithm that poisons a clean dataset by inserting the minimum number of missing values such that a test point is not certifiably robust for NBC. We prove that (iv) poisoning a clean dataset such that multiple test points become certifiably non-robust is NP-hard for any dataset with at least three features. Our experiments demonstrate that our algorithms for the decision and data poisoning problems achieve up to $19.5\times$ and $3.06\times$ speed-up over the baseline algorithms across different real-world datasets.

Streaming dynamic and distributed inference of latent geometric structures

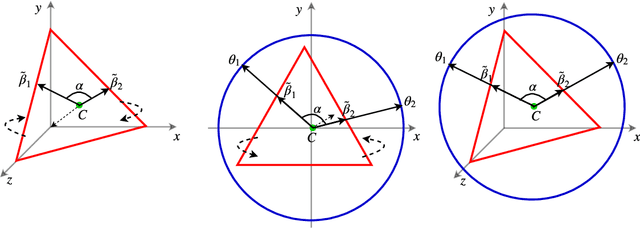
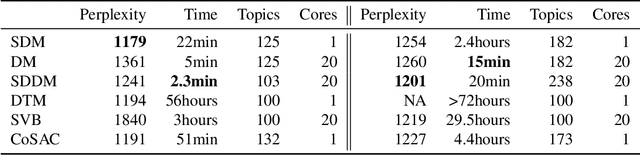
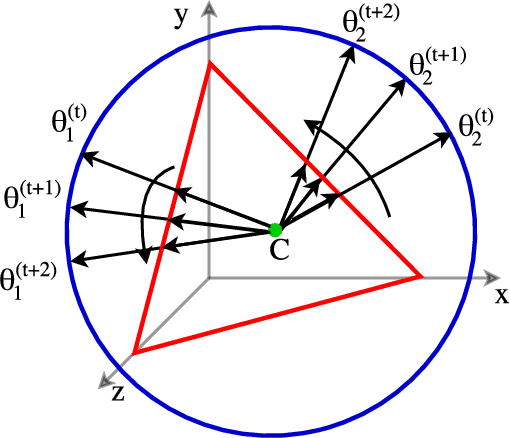
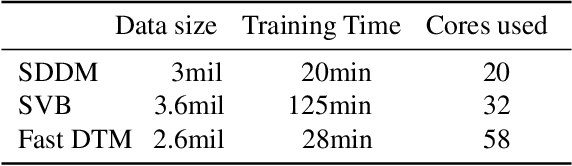
We develop new models and algorithms for learning the temporal dynamics of the topic polytopes and related geometric objects that arise in topic model based inference. Our model is nonparametric Bayesian and the corresponding inference algorithm is able to discover new topics as the time progresses. By exploiting the connection between the modeling of topic polytope evolution, Beta-Bernoulli process and the Hungarian matching algorithm, our method is shown to be several orders of magnitude faster than existing topic modeling approaches, as demonstrated by experiments working with several million documents in a dozen minutes.