Paraschos Koutris
Certifiable Robustness for Naive Bayes Classifiers
Mar 08, 2023Abstract:Data cleaning is crucial but often laborious in most machine learning (ML) applications. However, task-agnostic data cleaning is sometimes unnecessary if certain inconsistencies in the dirty data will not affect the prediction of ML models to the test points. A test point is certifiably robust for an ML classifier if the prediction remains the same regardless of which (among exponentially many) cleaned dataset it is trained on. In this paper, we study certifiable robustness for the Naive Bayes classifier (NBC) on dirty datasets with missing values. We present (i) a linear time algorithm in the number of entries in the dataset that decides whether a test point is certifiably robust for NBC, (ii) an algorithm that counts for each label, the number of cleaned datasets on which the NBC can be trained to predict that label, and (iii) an efficient optimal algorithm that poisons a clean dataset by inserting the minimum number of missing values such that a test point is not certifiably robust for NBC. We prove that (iv) poisoning a clean dataset such that multiple test points become certifiably non-robust is NP-hard for any dataset with at least three features. Our experiments demonstrate that our algorithms for the decision and data poisoning problems achieve up to $19.5\times$ and $3.06\times$ speed-up over the baseline algorithms across different real-world datasets.
Certifiable Robustness for Nearest Neighbor Classifiers
Jan 17, 2022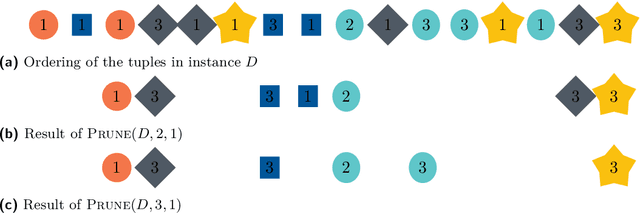
Abstract:ML models are typically trained using large datasets of high quality. However, training datasets often contain inconsistent or incomplete data. To tackle this issue, one solution is to develop algorithms that can check whether a prediction of a model is certifiably robust. Given a learning algorithm that produces a classifier and given an example at test time, a classification outcome is certifiably robust if it is predicted by every model trained across all possible worlds (repairs) of the uncertain (inconsistent) dataset. This notion of robustness falls naturally under the framework of certain answers. In this paper, we study the complexity of certifying robustness for a simple but widely deployed classification algorithm, $k$-Nearest Neighbors ($k$-NN). Our main focus is on inconsistent datasets when the integrity constraints are functional dependencies (FDs). For this setting, we establish a dichotomy in the complexity of certifying robustness w.r.t. the set of FDs: the problem either admits a polynomial time algorithm, or it is coNP-hard. Additionally, we exhibit a similar dichotomy for the counting version of the problem, where the goal is to count the number of possible worlds that predict a certain label. As a byproduct of our study, we also establish the complexity of a problem related to finding an optimal subset repair that may be of independent interest.
Streaming dynamic and distributed inference of latent geometric structures
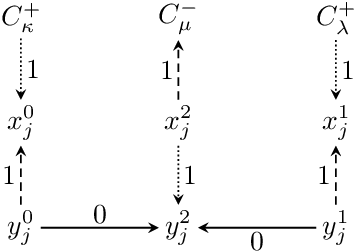
Sep 24, 2018
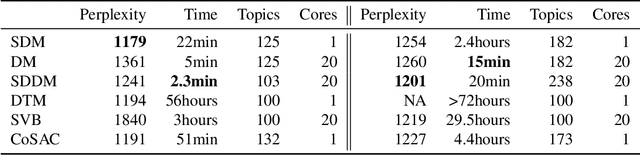
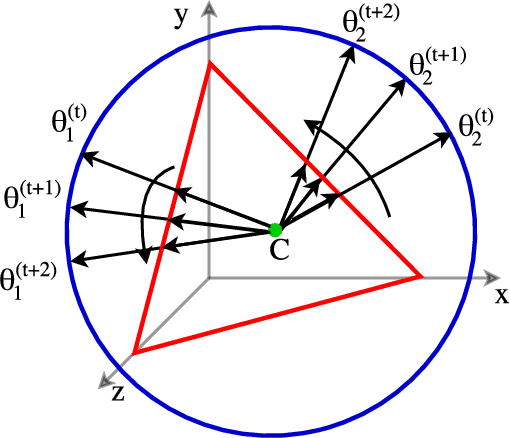
Abstract:We develop new models and algorithms for learning the temporal dynamics of the topic polytopes and related geometric objects that arise in topic model based inference. Our model is nonparametric Bayesian and the corresponding inference algorithm is able to discover new topics as the time progresses. By exploiting the connection between the modeling of topic polytope evolution, Beta-Bernoulli process and the Hungarian matching algorithm, our method is shown to be several orders of magnitude faster than existing topic modeling approaches, as demonstrated by experiments working with several million documents in a dozen minutes.
The Effect of Network Width on the Performance of Large-batch Training
Jun 11, 2018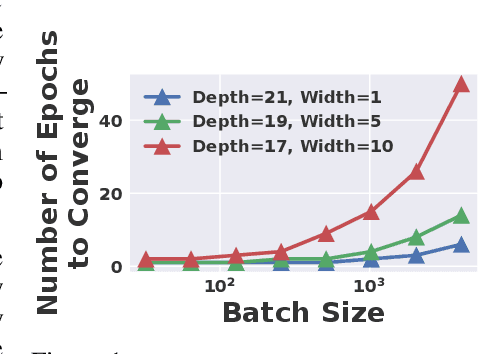
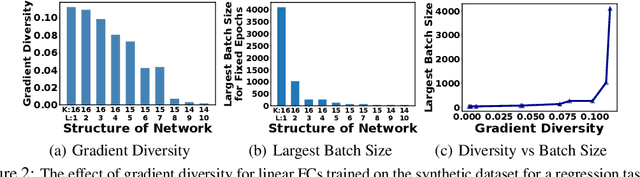
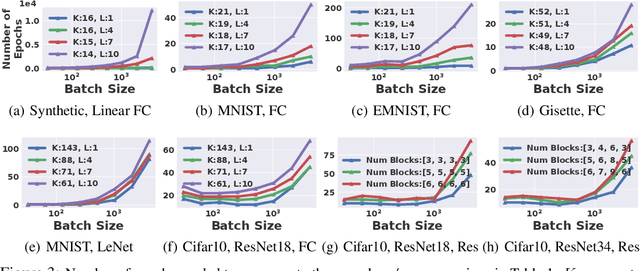
Abstract:Distributed implementations of mini-batch stochastic gradient descent (SGD) suffer from communication overheads, attributed to the high frequency of gradient updates inherent in small-batch training. Training with large batches can reduce these overheads; however, large batches can affect the convergence properties and generalization performance of SGD. In this work, we take a first step towards analyzing how the structure (width and depth) of a neural network affects the performance of large-batch training. We present new theoretical results which suggest that--for a fixed number of parameters--wider networks are more amenable to fast large-batch training compared to deeper ones. We provide extensive experiments on residual and fully-connected neural networks which suggest that wider networks can be trained using larger batches without incurring a convergence slow-down, unlike their deeper variants.
Model-based Pricing for Machine Learning in a Data Marketplace
May 26, 2018
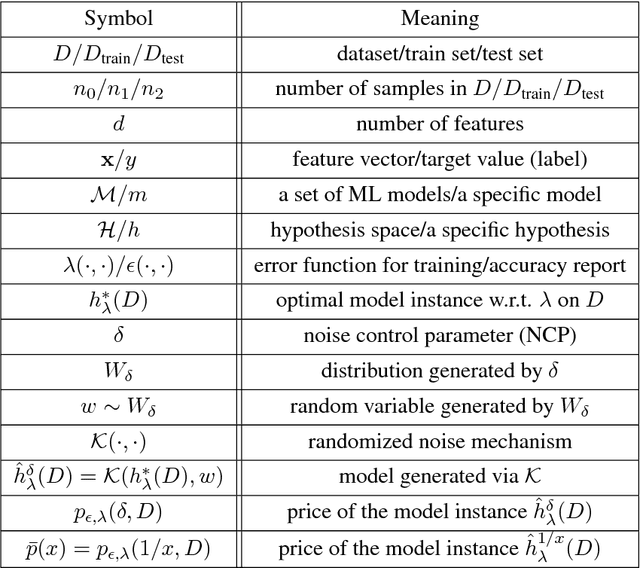


Abstract:Data analytics using machine learning (ML) has become ubiquitous in science, business intelligence, journalism and many other domains. While a lot of work focuses on reducing the training cost, inference runtime and storage cost of ML models, little work studies how to reduce the cost of data acquisition, which potentially leads to a loss of sellers' revenue and buyers' affordability and efficiency. In this paper, we propose a model-based pricing (MBP) framework, which instead of pricing the data, directly prices ML model instances. We first formally describe the desired properties of the MBP framework, with a focus on avoiding arbitrage. Next, we show a concrete realization of the MBP framework via a noise injection approach, which provably satisfies the desired formal properties. Based on the proposed framework, we then provide algorithmic solutions on how the seller can assign prices to models under different market scenarios (such as to maximize revenue). Finally, we conduct extensive experiments, which validate that the MBP framework can provide high revenue to the seller, high affordability to the buyer, and also operate on low runtime cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge