Stop Walking in Circles! Bailing Out Early in Projected Gradient Descent

Projected Gradient Descent (PGD) under the $L_\infty$ ball has become one of the defacto methods used in adversarial robustness evaluation for computer vision (CV) due to its reliability and efficacy, making a strong and easy-to-implement iterative baseline. However, PGD is computationally demanding to apply, especially when using thousands of iterations is the current best-practice recommendation to generate an adversarial example for a single image. In this work, we introduce a simple novel method for early termination of PGD based on cycle detection by exploiting the geometry of how PGD is implemented in practice and show that it can produce large speedup factors while providing the \emph{exact} same estimate of model robustness as standard PGD. This method substantially speeds up PGD without sacrificing any attack strength, enabling evaluations of robustness that were previously computationally intractable.

Differentially Private Iterative Screening Rules for Linear Regression

Linear $L_1$-regularized models have remained one of the simplest and most effective tools in data science. Over the past decade, screening rules have risen in popularity as a way to eliminate features when producing the sparse regression weights of $L_1$ models. However, despite the increasing need of privacy-preserving models for data analysis, to the best of our knowledge, no differentially private screening rule exists. In this paper, we develop the first private screening rule for linear regression. We initially find that this screening rule is too strong: it screens too many coefficients as a result of the private screening step. However, a weakened implementation of private screening reduces overscreening and improves performance.

Multi-layer Radial Basis Function Networks for Out-of-distribution Detection

Existing methods for out-of-distribution (OOD) detection use various techniques to produce a score, separate from classification, that determines how ``OOD'' an input is. Our insight is that OOD detection can be simplified by using a neural network architecture which can effectively merge classification and OOD detection into a single step. Radial basis function networks (RBFNs) inherently link classification confidence and OOD detection; however, these networks have lost popularity due to the difficult of training them in a multi-layer fashion. In this work, we develop a multi-layer radial basis function network (MLRBFN) which can be easily trained. To ensure that these networks are also effective for OOD detection, we develop a novel depression mechanism. We apply MLRBFNs as standalone classifiers and as heads on top of pretrained feature extractors, and find that they are competitive with commonly used methods for OOD detection. Our MLRBFN architecture demonstrates a promising new direction for OOD detection methods.

Position: Challenges and Opportunities for Differential Privacy in the U.S. Federal Government

In this article, we seek to elucidate challenges and opportunities for differential privacy within the federal government setting, as seen by a team of differential privacy researchers, privacy lawyers, and data scientists working closely with the U.S. government. After introducing differential privacy, we highlight three significant challenges which currently restrict the use of differential privacy in the U.S. government. We then provide two examples where differential privacy can enhance the capabilities of government agencies. The first example highlights how the quantitative nature of differential privacy allows policy security officers to release multiple versions of analyses with different levels of privacy. The second example, which we believe is a novel realization, indicates that differential privacy can be used to improve staffing efficiency in classified applications. We hope that this article can serve as a nontechnical resource which can help frame future action from the differential privacy community, privacy regulators, security officers, and lawmakers.

Feature Selection from Differentially Private Correlations

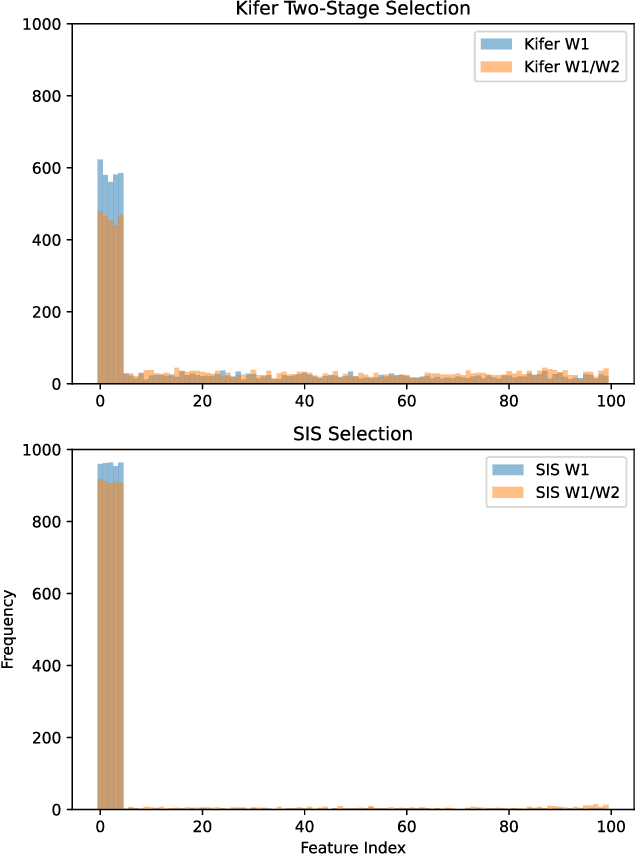
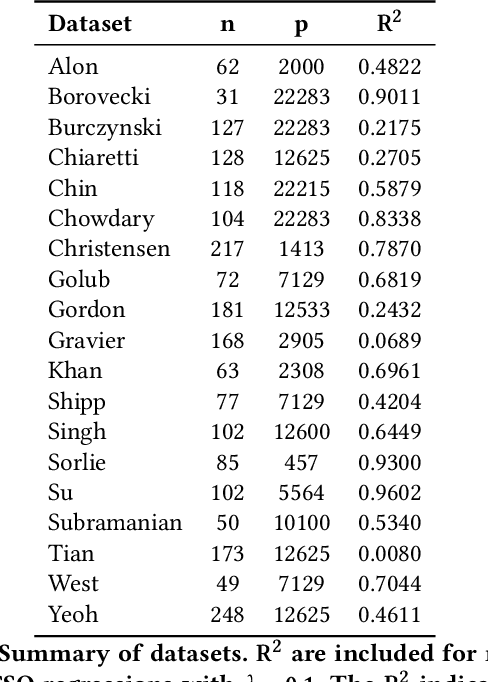
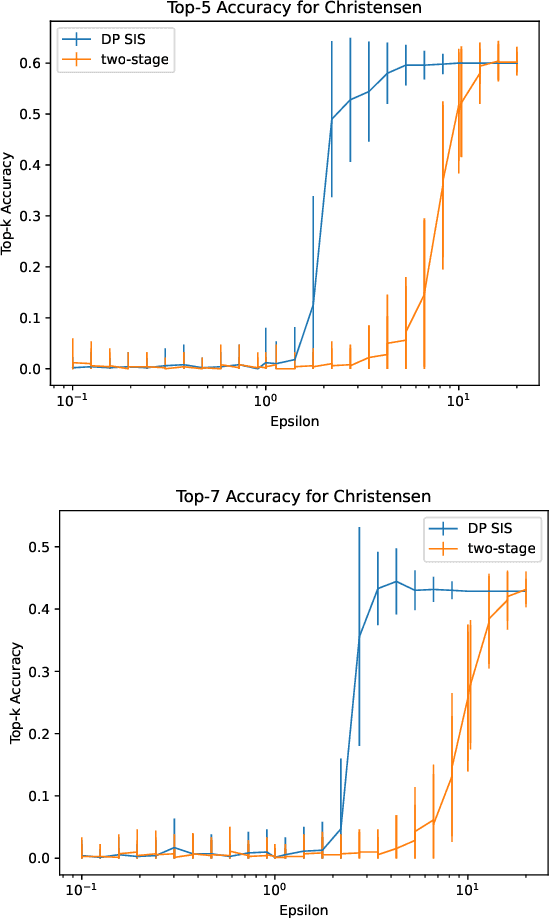
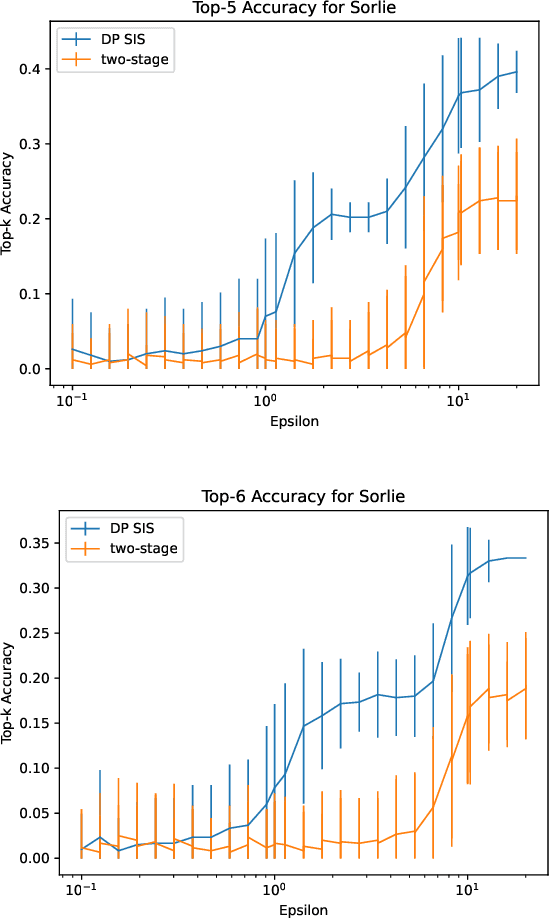
Data scientists often seek to identify the most important features in high-dimensional datasets. This can be done through $L_1$-regularized regression, but this can become inefficient for very high-dimensional datasets. Additionally, high-dimensional regression can leak information about individual datapoints in a dataset. In this paper, we empirically evaluate the established baseline method for feature selection with differential privacy, the two-stage selection technique, and show that it is not stable under sparsity. This makes it perform poorly on real-world datasets, so we consider a different approach to private feature selection. We employ a correlations-based order statistic to choose important features from a dataset and privatize them to ensure that the results do not leak information about individual datapoints. We find that our method significantly outperforms the established baseline for private feature selection on many datasets.

SoK: A Review of Differentially Private Linear Models For High-Dimensional Data

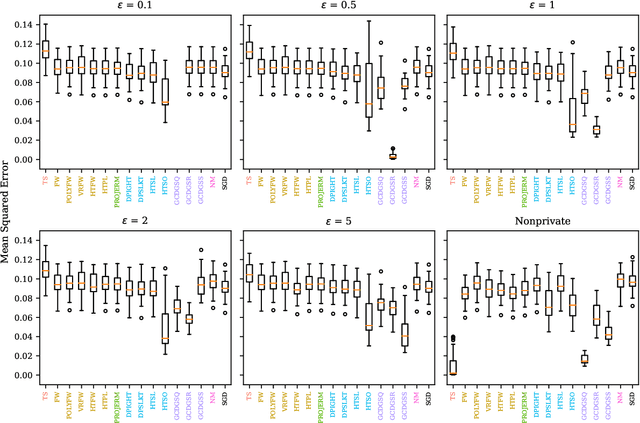
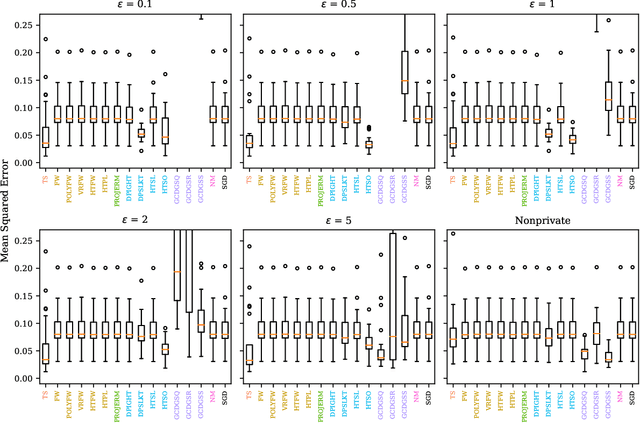
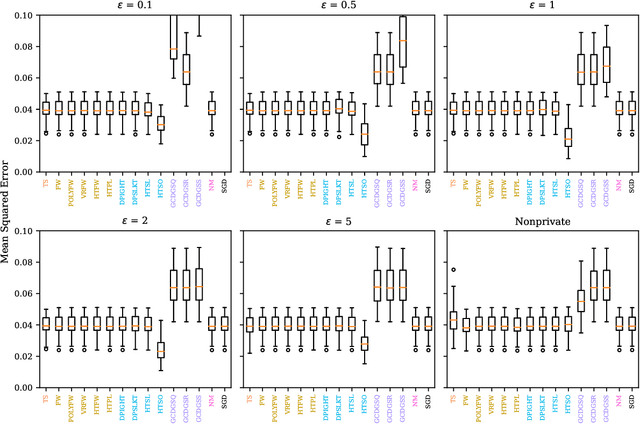
Linear models are ubiquitous in data science, but are particularly prone to overfitting and data memorization in high dimensions. To guarantee the privacy of training data, differential privacy can be used. Many papers have proposed optimization techniques for high-dimensional differentially private linear models, but a systematic comparison between these methods does not exist. We close this gap by providing a comprehensive review of optimization methods for private high-dimensional linear models. Empirical tests on all methods demonstrate robust and coordinate-optimized algorithms perform best, which can inform future research. Code for implementing all methods is released online.

Comprehensive OOD Detection Improvements

As machine learning becomes increasingly prevalent in impactful decisions, recognizing when inference data is outside the model's expected input distribution is paramount for giving context to predictions. Out-of-distribution (OOD) detection methods have been created for this task. Such methods can be split into representation-based or logit-based methods from whether they respectively utilize the model's embeddings or predictions for OOD detection. In contrast to most papers which solely focus on one such group, we address both. We employ dimensionality reduction on feature embeddings in representation-based methods for both time speedups and improved performance. Additionally, we propose DICE-COL, a modification of the popular logit-based method Directed Sparsification (DICE) that resolves an unnoticed flaw. We demonstrate the effectiveness of our methods on the OpenOODv1.5 benchmark framework, where they significantly improve performance and set state-of-the-art results.

Scaling Up Differentially Private LASSO Regularized Logistic Regression via Faster Frank-Wolfe Iterations

To the best of our knowledge, there are no methods today for training differentially private regression models on sparse input data. To remedy this, we adapt the Frank-Wolfe algorithm for $L_1$ penalized linear regression to be aware of sparse inputs and to use them effectively. In doing so, we reduce the training time of the algorithm from $\mathcal{O}( T D S + T N S)$ to $\mathcal{O}(N S + T \sqrt{D} \log{D} + T S^2)$, where $T$ is the number of iterations and a sparsity rate $S$ of a dataset with $N$ rows and $D$ features. Our results demonstrate that this procedure can reduce runtime by a factor of up to $2,200\times$, depending on the value of the privacy parameter $\epsilon$ and the sparsity of the dataset.

Sparse Private LASSO Logistic Regression

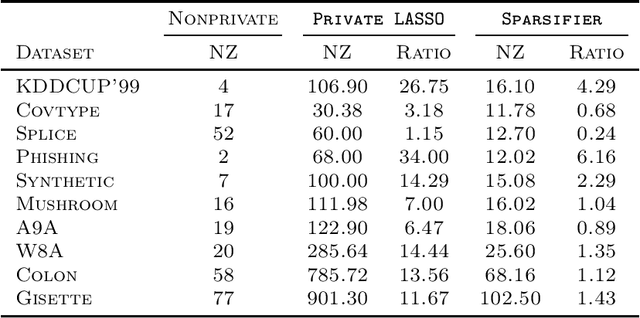
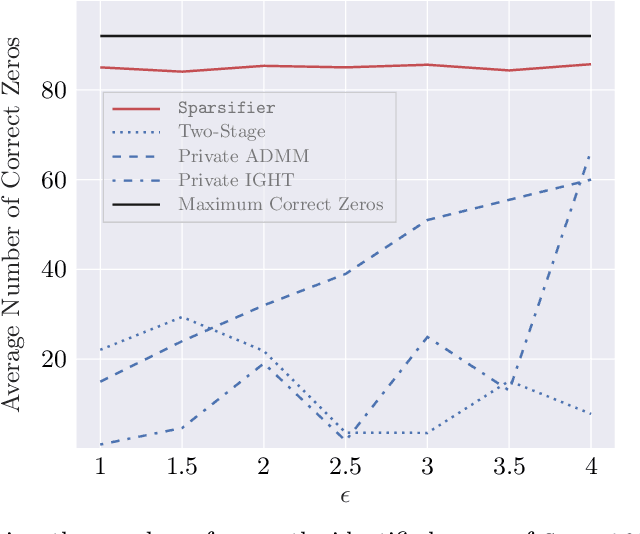
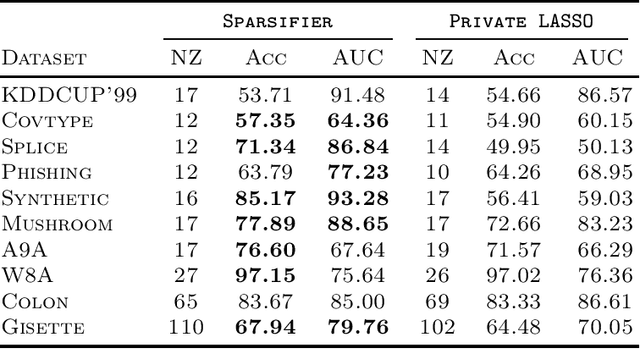
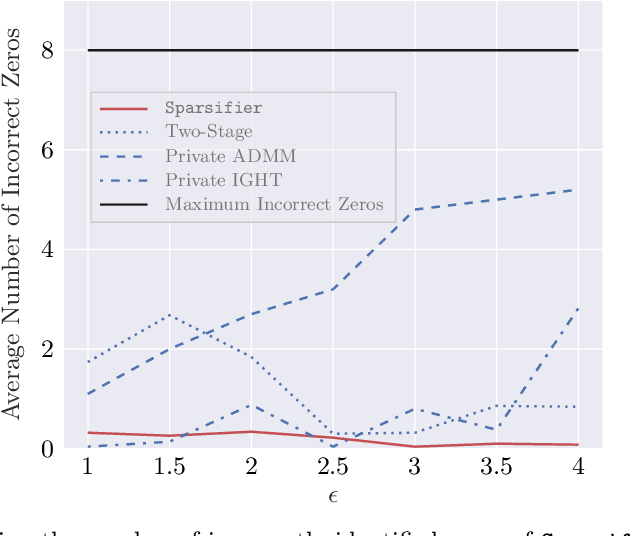
LASSO regularized logistic regression is particularly useful for its built-in feature selection, allowing coefficients to be removed from deployment and producing sparse solutions. Differentially private versions of LASSO logistic regression have been developed, but generally produce dense solutions, reducing the intrinsic utility of the LASSO penalty. In this paper, we present a differentially private method for sparse logistic regression that maintains hard zeros. Our key insight is to first train a non-private LASSO logistic regression model to determine an appropriate privatized number of non-zero coefficients to use in final model selection. To demonstrate our method's performance, we run experiments on synthetic and real-world datasets.

The Challenge of Differentially Private Screening Rules

Linear $L_1$-regularized models have remained one of the simplest and most effective tools in data analysis, especially in information retrieval problems where n-grams over text with TF-IDF or Okapi feature values are a strong and easy baseline. Over the past decade, screening rules have risen in popularity as a way to reduce the runtime for producing the sparse regression weights of $L_1$ models. However, despite the increasing need of privacy-preserving models in information retrieval, to the best of our knoweledge, no differentially private screening rule exists. In this paper, we develop the first differentially private screening rule for linear and logistic regression. In doing so, we discover difficulties in the task of making a useful private screening rule due to the amount of noise added to ensure privacy. We provide theoretical arguments and experimental evidence that this difficulty arises from the screening step itself and not the private optimizer. Based on our results, we highlight that developing an effective private $L_1$ screening method is an open problem in the differential privacy literature.