Differentially Private Iterative Screening Rules for Linear Regression

Linear $L_1$-regularized models have remained one of the simplest and most effective tools in data science. Over the past decade, screening rules have risen in popularity as a way to eliminate features when producing the sparse regression weights of $L_1$ models. However, despite the increasing need of privacy-preserving models for data analysis, to the best of our knowledge, no differentially private screening rule exists. In this paper, we develop the first private screening rule for linear regression. We initially find that this screening rule is too strong: it screens too many coefficients as a result of the private screening step. However, a weakened implementation of private screening reduces overscreening and improves performance.

Living off the Analyst: Harvesting Features from Yara Rules for Malware Detection

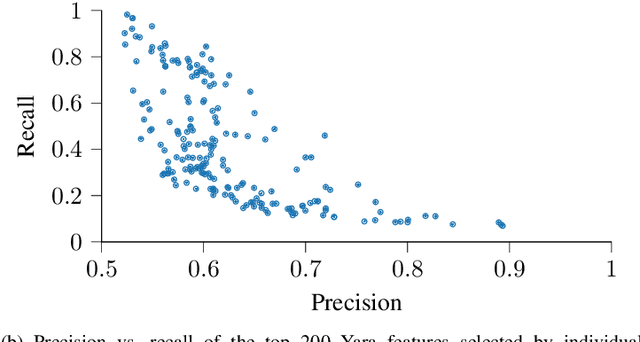
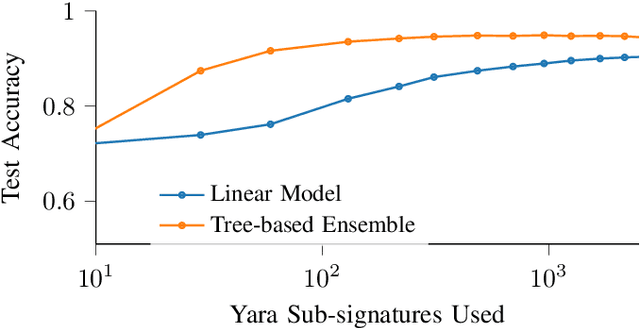
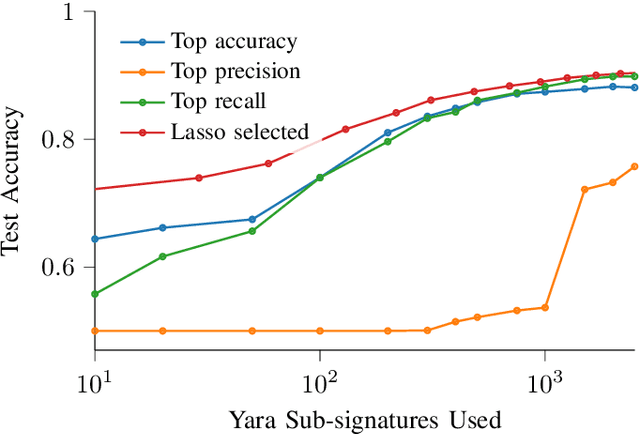
A strategy used by malicious actors is to "live off the land," where benign systems and tools already available on a victim's systems are used and repurposed for the malicious actor's intent. In this work, we ask if there is a way for anti-virus developers to similarly re-purpose existing work to improve their malware detection capability. We show that this is plausible via YARA rules, which use human-written signatures to detect specific malware families, functionalities, or other markers of interest. By extracting sub-signatures from publicly available YARA rules, we assembled a set of features that can more effectively discriminate malicious samples from benign ones. Our experiments demonstrate that these features add value beyond traditional features on the EMBER 2018 dataset. Manual analysis of the added sub-signatures shows a power-law behavior in a combination of features that are specific and unique, as well as features that occur often. A prior expectation may be that the features would be limited in being overly specific to unique malware families. This behavior is observed, and is apparently useful in practice. In addition, we also find sub-signatures that are dual-purpose (e.g., detecting virtual machine environments) or broadly generic (e.g., DLL imports).

Stabilizing Linear Passive-Aggressive Online Learning with Weighted Reservoir Sampling

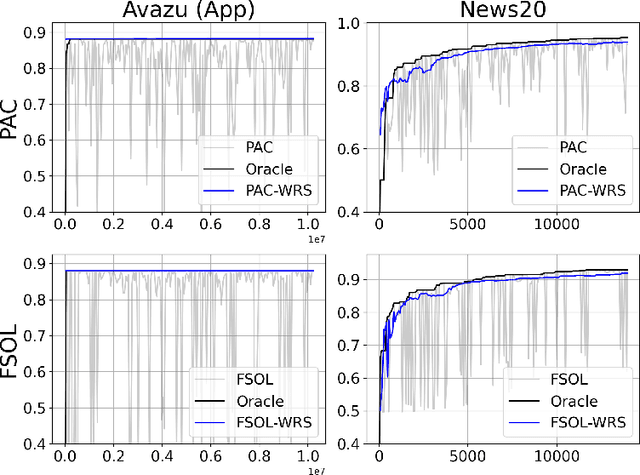
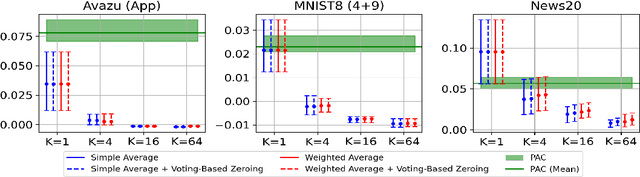
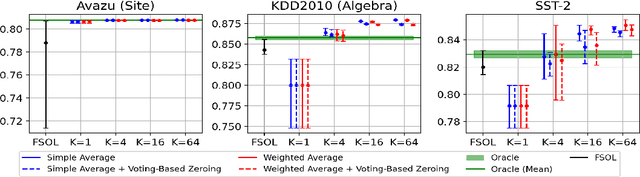
Online learning methods, like the seminal Passive-Aggressive (PA) classifier, are still highly effective for high-dimensional streaming data, out-of-core processing, and other throughput-sensitive applications. Many such algorithms rely on fast adaptation to individual errors as a key to their convergence. While such algorithms enjoy low theoretical regret, in real-world deployment they can be sensitive to individual outliers that cause the algorithm to over-correct. When such outliers occur at the end of the data stream, this can cause the final solution to have unexpectedly low accuracy. We design a weighted reservoir sampling (WRS) approach to obtain a stable ensemble model from the sequence of solutions without requiring additional passes over the data, hold-out sets, or a growing amount of memory. Our key insight is that good solutions tend to be error-free for more iterations than bad solutions, and thus, the number of passive rounds provides an estimate of a solution's relative quality. Our reservoir thus contains $K$ previous intermediate weight vectors with high survival times. We demonstrate our WRS approach on the Passive-Aggressive Classifier (PAC) and First-Order Sparse Online Learning (FSOL), where our method consistently and significantly outperforms the unmodified approach. We show that the risk of the ensemble classifier is bounded with respect to the regret of the underlying online learning method.

High-Dimensional Distributed Sparse Classification with Scalable Communication-Efficient Global Updates

As the size of datasets used in statistical learning continues to grow, distributed training of models has attracted increasing attention. These methods partition the data and exploit parallelism to reduce memory and runtime, but suffer increasingly from communication costs as the data size or the number of iterations grows. Recent work on linear models has shown that a surrogate likelihood can be optimized locally to iteratively improve on an initial solution in a communication-efficient manner. However, existing versions of these methods experience multiple shortcomings as the data size becomes massive, including diverging updates and efficiently handling sparsity. In this work we develop solutions to these problems which enable us to learn a communication-efficient distributed logistic regression model even beyond millions of features. In our experiments we demonstrate a large improvement in accuracy over distributed algorithms with only a few distributed update steps needed, and similar or faster runtimes. Our code is available at \url{https://github.com/FutureComputing4AI/ProxCSL}.

Optimizing the Optimal Weighted Average: Efficient Distributed Sparse Classification

While distributed training is often viewed as a solution to optimizing linear models on increasingly large datasets, inter-machine communication costs of popular distributed approaches can dominate as data dimensionality increases. Recent work on non-interactive algorithms shows that approximate solutions for linear models can be obtained efficiently with only a single round of communication among machines. However, this approximation often degenerates as the number of machines increases. In this paper, building on the recent optimal weighted average method, we introduce a new technique, ACOWA, that allows an extra round of communication to achieve noticeably better approximation quality with minor runtime increases. Results show that for sparse distributed logistic regression, ACOWA obtains solutions that are more faithful to the empirical risk minimizer and attain substantially higher accuracy than other distributed algorithms.

Small Effect Sizes in Malware Detection? Make Harder Train/Test Splits!

Industry practitioners care about small improvements in malware detection accuracy because their models are deployed to hundreds of millions of machines, meaning a 0.1\% change can cause an overwhelming number of false positives. However, academic research is often restrained to public datasets on the order of ten thousand samples and is too small to detect improvements that may be relevant to industry. Working within these constraints, we devise an approach to generate a benchmark of configurable difficulty from a pool of available samples. This is done by leveraging malware family information from tools like AVClass to construct training/test splits that have different generalization rates, as measured by a secondary model. Our experiments will demonstrate that using a less accurate secondary model with disparate features is effective at producing benchmarks for a more sophisticated target model that is under evaluation. We also ablate against alternative designs to show the need for our approach.

Scaling Up Differentially Private LASSO Regularized Logistic Regression via Faster Frank-Wolfe Iterations

To the best of our knowledge, there are no methods today for training differentially private regression models on sparse input data. To remedy this, we adapt the Frank-Wolfe algorithm for $L_1$ penalized linear regression to be aware of sparse inputs and to use them effectively. In doing so, we reduce the training time of the algorithm from $\mathcal{O}( T D S + T N S)$ to $\mathcal{O}(N S + T \sqrt{D} \log{D} + T S^2)$, where $T$ is the number of iterations and a sparsity rate $S$ of a dataset with $N$ rows and $D$ features. Our results demonstrate that this procedure can reduce runtime by a factor of up to $2,200\times$, depending on the value of the privacy parameter $\epsilon$ and the sparsity of the dataset.

Exploring the Sharpened Cosine Similarity

Convolutional layers have long served as the primary workhorse for image classification. Recently, an alternative to convolution was proposed using the Sharpened Cosine Similarity (SCS), which in theory may serve as a better feature detector. While multiple sources report promising results, there has not been to date a full-scale empirical analysis of neural network performance using these new layers. In our work, we explore SCS's parameter behavior and potential as a drop-in replacement for convolutions in multiple CNN architectures benchmarked on CIFAR-10. We find that while SCS may not yield significant increases in accuracy, it may learn more interpretable representations. We also find that, in some circumstances, SCS may confer a slight increase in adversarial robustness.

Probing the Transition to Dataset-Level Privacy in ML Models Using an Output-Specific and Data-Resolved Privacy Profile

Differential privacy (DP) is the prevailing technique for protecting user data in machine learning models. However, deficits to this framework include a lack of clarity for selecting the privacy budget $\epsilon$ and a lack of quantification for the privacy leakage for a particular data row by a particular trained model. We make progress toward these limitations and a new perspective by which to visualize DP results by studying a privacy metric that quantifies the extent to which a model trained on a dataset using a DP mechanism is ``covered" by each of the distributions resulting from training on neighboring datasets. We connect this coverage metric to what has been established in the literature and use it to rank the privacy of individual samples from the training set in what we call a privacy profile. We additionally show that the privacy profile can be used to probe an observed transition to indistinguishability that takes place in the neighboring distributions as $\epsilon$ decreases, which we suggest is a tool that can enable the selection of $\epsilon$ by the ML practitioner wishing to make use of DP.

Sparse Private LASSO Logistic Regression

LASSO regularized logistic regression is particularly useful for its built-in feature selection, allowing coefficients to be removed from deployment and producing sparse solutions. Differentially private versions of LASSO logistic regression have been developed, but generally produce dense solutions, reducing the intrinsic utility of the LASSO penalty. In this paper, we present a differentially private method for sparse logistic regression that maintains hard zeros. Our key insight is to first train a non-private LASSO logistic regression model to determine an appropriate privatized number of non-zero coefficients to use in final model selection. To demonstrate our method's performance, we run experiments on synthetic and real-world datasets.