Probing the Transition to Dataset-Level Privacy in ML Models Using an Output-Specific and Data-Resolved Privacy Profile

Differential privacy (DP) is the prevailing technique for protecting user data in machine learning models. However, deficits to this framework include a lack of clarity for selecting the privacy budget $\epsilon$ and a lack of quantification for the privacy leakage for a particular data row by a particular trained model. We make progress toward these limitations and a new perspective by which to visualize DP results by studying a privacy metric that quantifies the extent to which a model trained on a dataset using a DP mechanism is ``covered" by each of the distributions resulting from training on neighboring datasets. We connect this coverage metric to what has been established in the literature and use it to rank the privacy of individual samples from the training set in what we call a privacy profile. We additionally show that the privacy profile can be used to probe an observed transition to indistinguishability that takes place in the neighboring distributions as $\epsilon$ decreases, which we suggest is a tool that can enable the selection of $\epsilon$ by the ML practitioner wishing to make use of DP.

A General Framework for Auditing Differentially Private Machine Learning

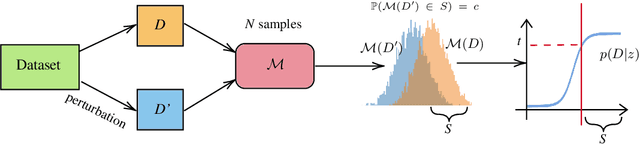
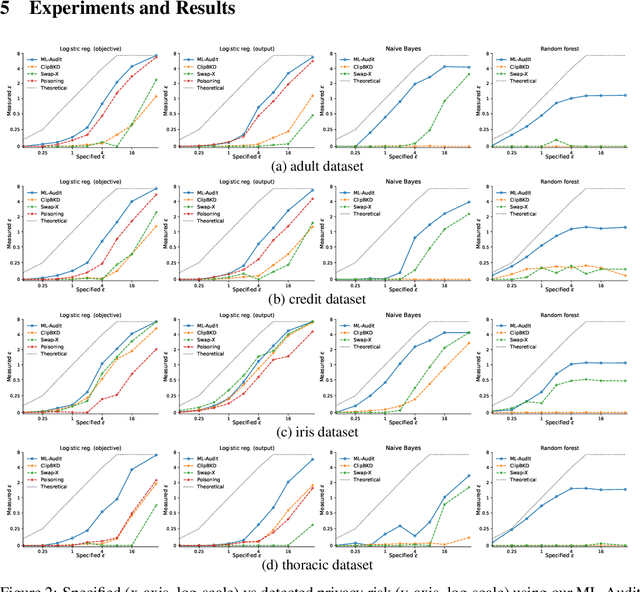
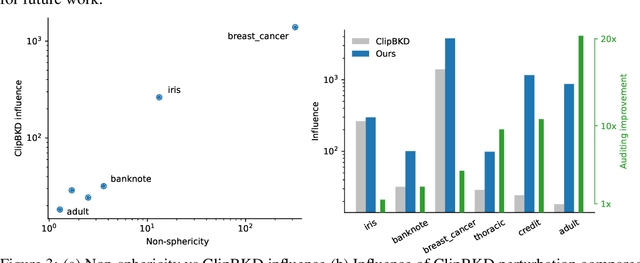
We present a framework to statistically audit the privacy guarantee conferred by a differentially private machine learner in practice. While previous works have taken steps toward evaluating privacy loss through poisoning attacks or membership inference, they have been tailored to specific models or have demonstrated low statistical power. Our work develops a general methodology to empirically evaluate the privacy of differentially private machine learning implementations, combining improved privacy search and verification methods with a toolkit of influence-based poisoning attacks. We demonstrate significantly improved auditing power over previous approaches on a variety of models including logistic regression, Naive Bayes, and random forest. Our method can be used to detect privacy violations due to implementation errors or misuse. When violations are not present, it can aid in understanding the amount of information that can be leaked from a given dataset, algorithm, and privacy specification.

An Algorithm for Approximating Continuous Functions on Compact Subsets with a Neural Network with one Hidden Layer

George Cybenko's landmark 1989 paper showed that there exists a feedforward neural network, with exactly one hidden layer (and a finite number of neurons), that can arbitrarily approximate a given continuous function $f$ on the unit hypercube. The paper did not address how to find the weight/parameters of such a network, or if finding them would be computationally feasible. This paper outlines an algorithm for a neural network with exactly one hidden layer to reconstruct any continuous scalar or vector valued continuous function.