Stabilizing Linear Passive-Aggressive Online Learning with Weighted Reservoir Sampling
Paper and Code
Oct 31, 2024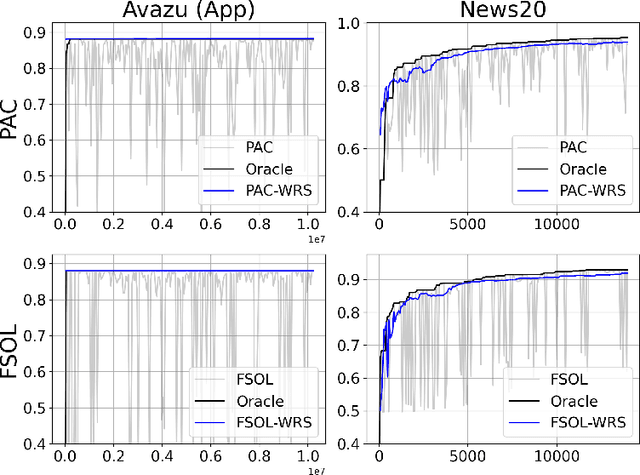
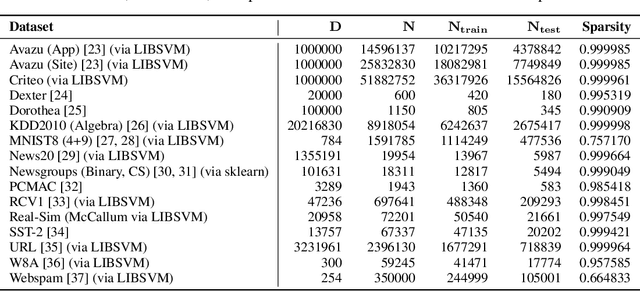
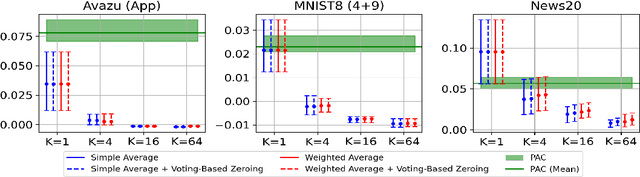
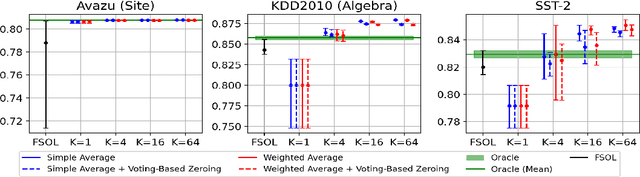
Online learning methods, like the seminal Passive-Aggressive (PA) classifier, are still highly effective for high-dimensional streaming data, out-of-core processing, and other throughput-sensitive applications. Many such algorithms rely on fast adaptation to individual errors as a key to their convergence. While such algorithms enjoy low theoretical regret, in real-world deployment they can be sensitive to individual outliers that cause the algorithm to over-correct. When such outliers occur at the end of the data stream, this can cause the final solution to have unexpectedly low accuracy. We design a weighted reservoir sampling (WRS) approach to obtain a stable ensemble model from the sequence of solutions without requiring additional passes over the data, hold-out sets, or a growing amount of memory. Our key insight is that good solutions tend to be error-free for more iterations than bad solutions, and thus, the number of passive rounds provides an estimate of a solution's relative quality. Our reservoir thus contains $K$ previous intermediate weight vectors with high survival times. We demonstrate our WRS approach on the Passive-Aggressive Classifier (PAC) and First-Order Sparse Online Learning (FSOL), where our method consistently and significantly outperforms the unmodified approach. We show that the risk of the ensemble classifier is bounded with respect to the regret of the underlying online learning method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge