CoLT: The conditional localization test for assessing the accuracy of neural posterior estimates

We consider the problem of validating whether a neural posterior estimate \( q(\theta \mid x) \) is an accurate approximation to the true, unknown true posterior \( p(\theta \mid x) \). Existing methods for evaluating the quality of an NPE estimate are largely derived from classifier-based tests or divergence measures, but these suffer from several practical drawbacks. As an alternative, we introduce the \emph{Conditional Localization Test} (CoLT), a principled method designed to detect discrepancies between \( p(\theta \mid x) \) and \( q(\theta \mid x) \) across the full range of conditioning inputs. Rather than relying on exhaustive comparisons or density estimation at every \( x \), CoLT learns a localization function that adaptively selects points $\theta_l(x)$ where the neural posterior $q$ deviates most strongly from the true posterior $p$ for that $x$. This approach is particularly advantageous in typical simulation-based inference settings, where only a single draw \( \theta \sim p(\theta \mid x) \) from the true posterior is observed for each conditioning input, but where the neural posterior \( q(\theta \mid x) \) can be sampled an arbitrary number of times. Our theoretical results establish necessary and sufficient conditions for assessing distributional equality across all \( x \), offering both rigorous guarantees and practical scalability. Empirically, we demonstrate that CoLT not only performs better than existing methods at comparing $p$ and $q$, but also pinpoints regions of significant divergence, providing actionable insights for model refinement. These properties position CoLT as a state-of-the-art solution for validating neural posterior estimates.

The surprising strength of weak classifiers for validating neural posterior estimates

Neural Posterior Estimation (NPE) has emerged as a powerful approach for amortized Bayesian inference when the true posterior $p(\theta \mid y)$ is intractable or difficult to sample. But evaluating the accuracy of neural posterior estimates remains challenging, with existing methods suffering from major limitations. One appealing and widely used method is the classifier two-sample test (C2ST), where a classifier is trained to distinguish samples from the true posterior $p(\theta \mid y)$ versus the learned NPE approximation $q(\theta \mid y)$. Yet despite the appealing simplicity of the C2ST, its theoretical and practical reliability depend upon having access to a near-Bayes-optimal classifier -- a requirement that is rarely met and, at best, difficult to verify. Thus a major open question is: can a weak classifier still be useful for neural posterior validation? We show that the answer is yes. Building on the work of Hu and Lei, we present several key results for a conformal variant of the C2ST, which converts any trained classifier's scores -- even those of weak or over-fitted models -- into exact finite-sample p-values. We establish two key theoretical properties of the conformal C2ST: (i) finite-sample Type-I error control, and (ii) non-trivial power that degrades gently in tandem with the error of the trained classifier. The upshot is that even weak, biased, or overfit classifiers can still yield powerful and reliable tests. Empirically, the Conformal C2ST outperforms classical discriminative tests across a wide range of benchmarks. These results reveal the under appreciated strength of weak classifiers for validating neural posterior estimates, establishing the conformal C2ST as a practical, theoretically grounded diagnostic for modern simulation-based inference.

Conditional diffusions for neural posterior estimation

Neural posterior estimation (NPE), a simulation-based computational approach for Bayesian inference, has shown great success in situations where posteriors are intractable or likelihood functions are treated as "black boxes." Existing NPE methods typically rely on normalizing flows, which transform a base distributions into a complex posterior by composing many simple, invertible transformations. But flow-based models, while state of the art for NPE, are known to suffer from several limitations, including training instability and sharp trade-offs between representational power and computational cost. In this work, we demonstrate the effectiveness of conditional diffusions as an alternative to normalizing flows for NPE. Conditional diffusions address many of the challenges faced by flow-based methods. Our results show that, across a highly varied suite of benchmarking problems for NPE architectures, diffusions offer improved stability, superior accuracy, and faster training times, even with simpler, shallower models. These gains persist across a variety of different encoder or "summary network" architectures, as well as in situations where no summary network is required. The code will be publicly available at \url{https://github.com/TianyuCodings/cDiff}.

Straightness of Rectified Flow: A Theoretical Insight into Wasserstein Convergence

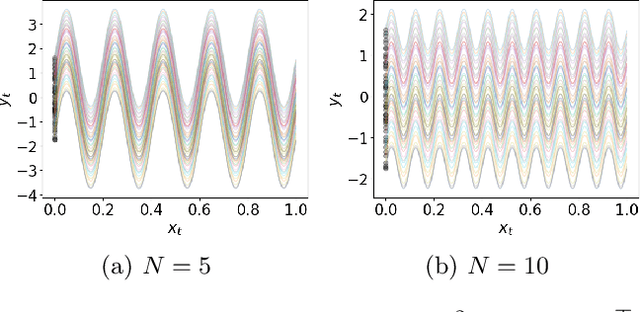
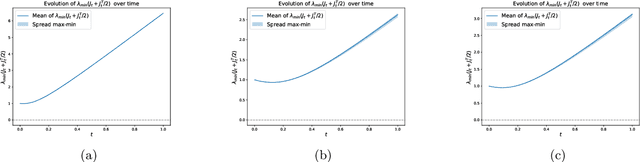
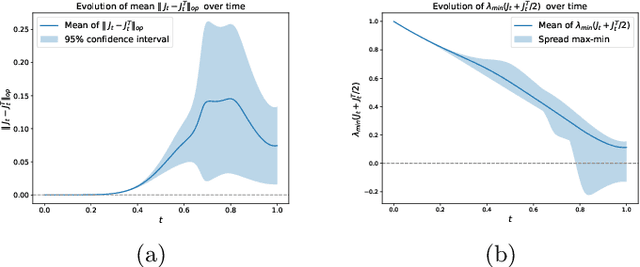
Diffusion models have emerged as a powerful tool for image generation and denoising. Typically, generative models learn a trajectory between the starting noise distribution and the target data distribution. Recently Liu et al. (2023b) designed a novel alternative generative model Rectified Flow (RF), which aims to learn straight flow trajectories from noise to data using a sequence of convex optimization problems with close ties to optimal transport. If the trajectory is curved, one must use many Euler discretization steps or novel strategies, such as exponential integrators, to achieve a satisfactory generation quality. In contrast, RF has been shown to theoretically straighten the trajectory through successive rectifications, reducing the number of function evaluations (NFEs) while sampling. It has also been shown empirically that RF may improve the straightness in two rectifications if one can solve the underlying optimization problem within a sufficiently small error. In this paper, we make two key theoretical contributions: 1) we provide the first theoretical analysis of the Wasserstein distance between the sampling distribution of RF and the target distribution. Our error rate is characterized by the number of discretization steps and a new formulation of straightness stronger than that in the original work. 2) In line with the previous empirical findings, we show that, for a rectified flow from a Gaussian to a mixture of two Gaussians, two rectifications are sufficient to achieve a straight flow. Additionally, we also present empirical results on both simulated and real datasets to validate our theoretical findings.