Low-power SNN-based audio source localisation using a Hilbert Transform spike encoding scheme

Sound source localisation is used in many consumer electronics devices, to help isolate audio from individual speakers and to reject noise. Localization is frequently accomplished by "beamforming" algorithms, which combine microphone audio streams to improve received signal power from particular incident source directions. Beamforming algorithms generally use knowledge of the frequency components of the audio source, along with the known microphone array geometry, to analytically phase-shift microphone streams before combining them. A dense set of band-pass filters is often used to obtain known-frequency "narrowband" components from wide-band audio streams. These approaches achieve high accuracy, but state of the art narrowband beamforming algorithms are computationally demanding, and are therefore difficult to integrate into low-power IoT devices. We demonstrate a novel method for sound source localisation in arbitrary microphone arrays, designed for efficient implementation in ultra-low-power spiking neural networks (SNNs). We use a novel short-time Hilbert transform (STHT) to remove the need for demanding band-pass filtering of audio, and introduce a new accompanying method for audio encoding with spiking events. Our beamforming and localisation approach achieves state-of-the-art accuracy for SNN methods, and comparable with traditional non-SNN super-resolution approaches. We deploy our method to low-power SNN audio inference hardware, and achieve much lower power consumption compared with super-resolution methods. We demonstrate that signal processing approaches can be co-designed with spiking neural network implementations to achieve high levels of power efficiency. Our new Hilbert-transform-based method for beamforming promises to also improve the efficiency of traditional DSP-based signal processing.

EXODUS: Stable and Efficient Training of Spiking Neural Networks

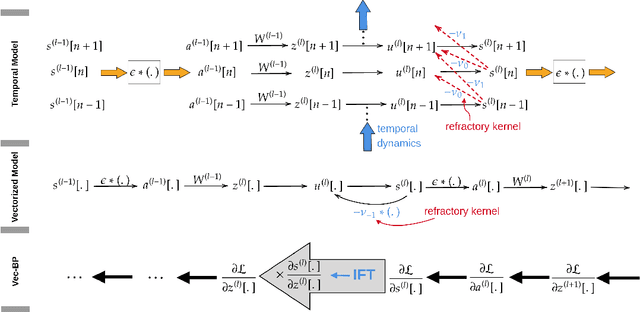
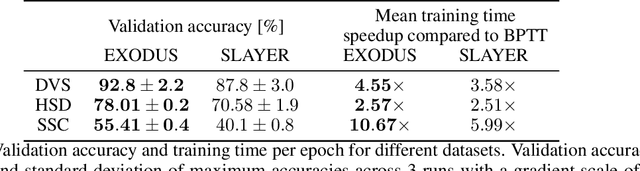
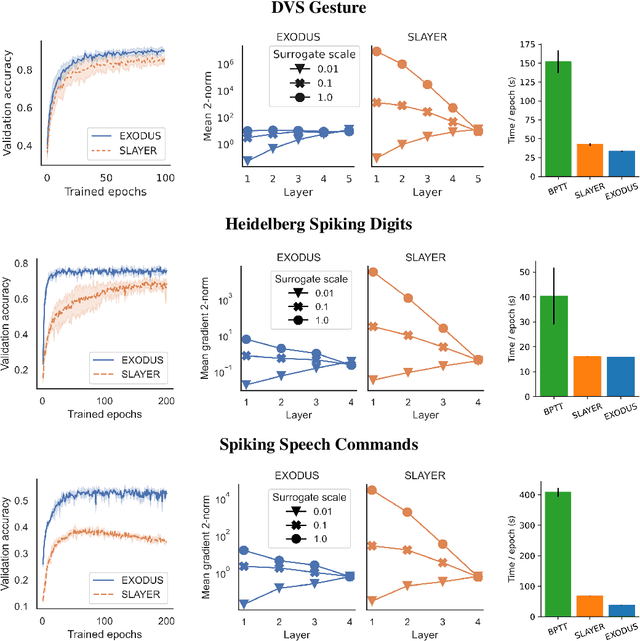
Spiking Neural Networks (SNNs) are gaining significant traction in machine learning tasks where energy-efficiency is of utmost importance. Training such networks using the state-of-the-art back-propagation through time (BPTT) is, however, very time-consuming. Previous work by Shrestha and Orchard [2018] employs an efficient GPU-accelerated back-propagation algorithm called SLAYER, which speeds up training considerably. SLAYER, however, does not take into account the neuron reset mechanism while computing the gradients, which we argue to be the source of numerical instability. To counteract this, SLAYER introduces a gradient scale hyperparameter across layers, which needs manual tuning. In this paper, (i) we modify SLAYER and design an algorithm called EXODUS, that accounts for the neuron reset mechanism and applies the Implicit Function Theorem (IFT) to calculate the correct gradients (equivalent to those computed by BPTT), (ii) we eliminate the need for ad-hoc scaling of gradients, thus, reducing the training complexity tremendously, (iii) we demonstrate, via computer simulations, that EXODUS is numerically stable and achieves a comparable or better performance than SLAYER especially in various tasks with SNNs that rely on temporal features. Our code is available at https://github.com/synsense/sinabs-exodus.

Machine Learning for Geometrically-Consistent Angular Spread Function Estimation in Massive MIMO

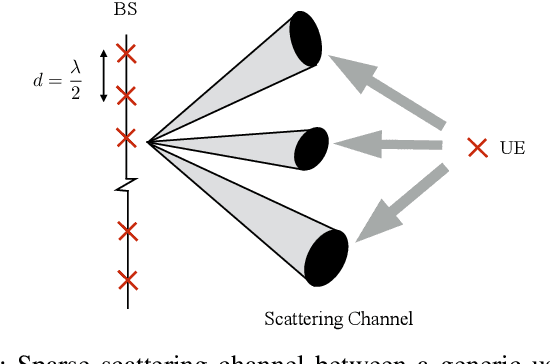
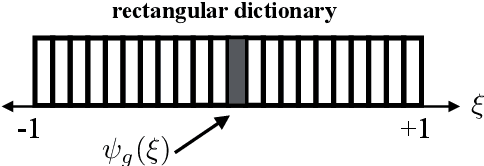
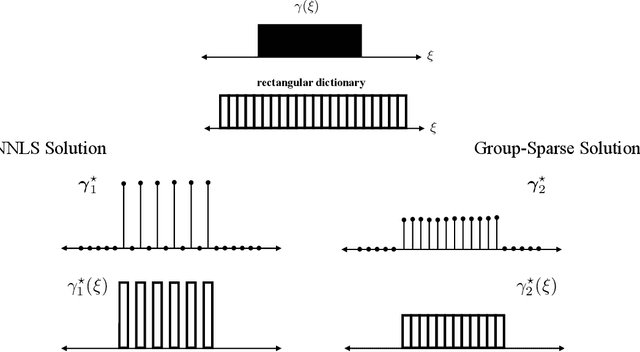
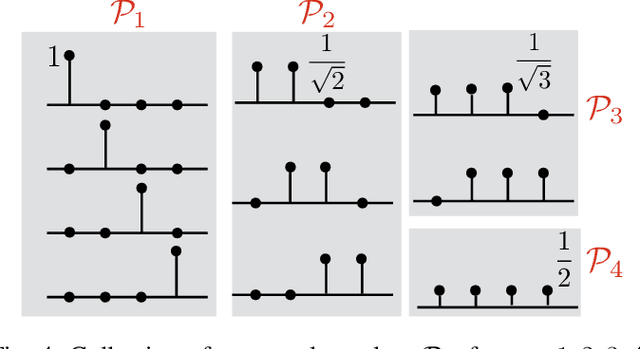
In the spatial channel models used in multi-antenna wireless communications, the propagation from a single-antenna transmitter (e.g., a user) to an M-antenna receiver (e.g., a Base Station) occurs through scattering clusters located in the far field of the receiving antenna array. The Angular Spread Function (ASF) of the corresponding M-dim channel vector describes the angular density of the received signal power at the array. The modern literature on massive MIMO has recognized that the knowledge of covariance matrix of user channel vectors is very useful for various applications such as hybrid digital analog beamforming, pilot decontamination, etc. Therefore, most literature has focused on the estimation of such channel covariance matrices. However, in some applications such as uplink-downlink covariance transformation (for FDD massive MIMO precoding) and channel sounding some form of ASF estimation is required either implicitly or explicitly. It turns out that while covariance estimation is well-known and well-conditioned, the ASF estimation is a much harder problem and is in general ill-posed. In this paper, we show that under additional geometrically-consistent group-sparsity structure on the ASF, which is prevalent in almost all wireless propagation scenarios, one is able to estimate ASF properly. We propose sparse dictionary-based algorithms that promote this group-sparsity structure via suitable regularizations. Since generally it is difficult to capture the notion of group-sparsity through proper regularization, we propose another algorithm based on Deep Neural Networks (DNNs) that learns this structure. We provide numerical simulations to assess the performance of our proposed algorithms. We also compare the results with that of other methods in the literature, where we re-frame those methods in the context of ASF estimation in massive MIMO.

Multiple Measurement Vectors Problem: A Decoupling Property and its Applications

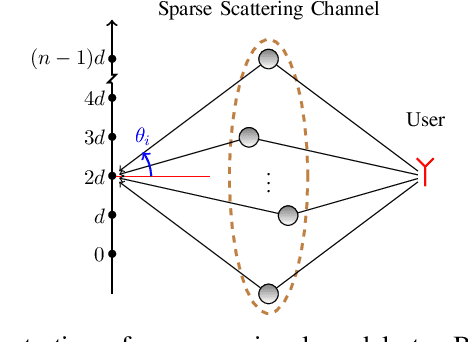
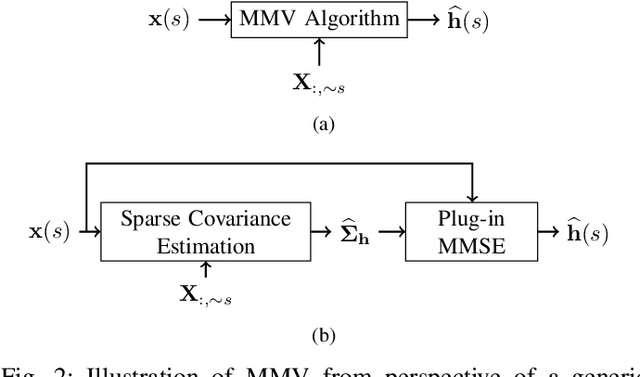
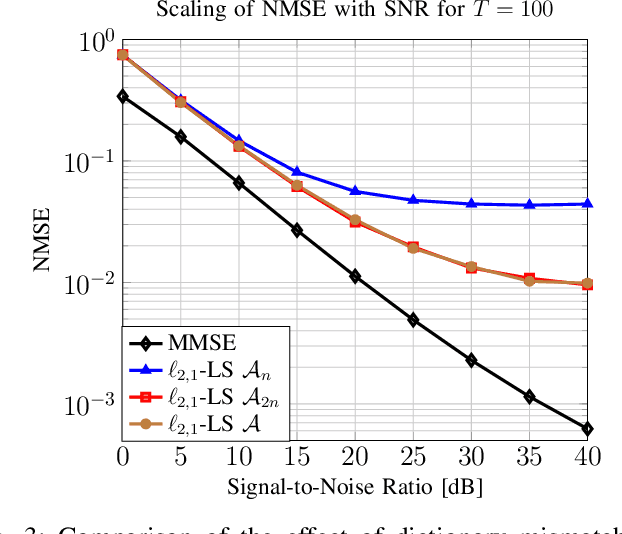
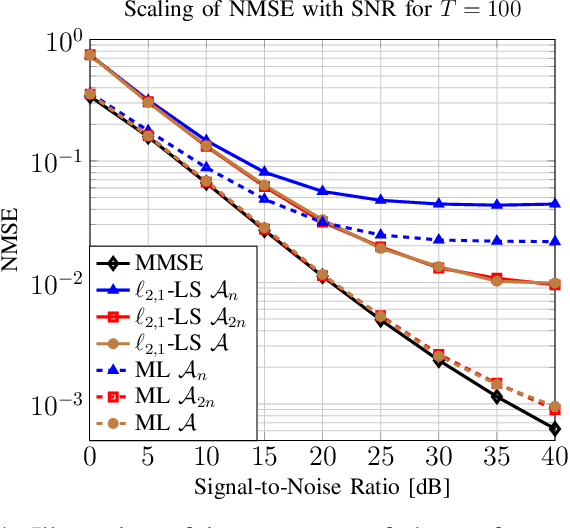
Efficient and reliable estimation in many signal processing problems encountered in applications requires adopting sparsity prior in a suitable basis on the signals and using techniques from compressed sensing (CS). In this paper, we study a CS problem known as Multiple Measurement Vectors (MMV) problem, which arises in joint estimation of multiple signal realizations when the signal samples have a common (joint) support over a fixed known dictionary. Although there is a vast literature on the analysis of MMV, it is not yet fully known how the number of signal samples and their statistical correlations affects the performance of the joint estimation in MMV. Moreover, in many instances of MMV the underlying sparsifying dictionary may not be precisely known, and it is still an open problem to quantify how the dictionary mismatch may affect the estimation performance. In this paper, we focus on $\ell_{2,1}$-norm regularized least squares ($\ell_{2,1}$-LS) as a well-known and widely-used MMV algorithm in the literature. We prove an interesting decoupling property for $\ell_{2,1}$-LS, where we show that it can be decomposed into two phases: i) use all the signal samples to estimate the signal covariance matrix (coupled phase), ii) plug in the resulting covariance estimate as the true covariance matrix into the Minimum Mean Squared Error (MMSE) estimator to reconstruct each signal sample individually (decoupled phase). As a consequence of this decomposition, we are able to provide further insights on the performance of $\ell_{2,1}$-LS for MMV. In particular, we address how the signal correlations and dictionary mismatch affects its estimation performance. We also provide numerical simulations to validate our theoretical results.

Multi-Band Covariance Interpolation with Applications in Massive MIMO

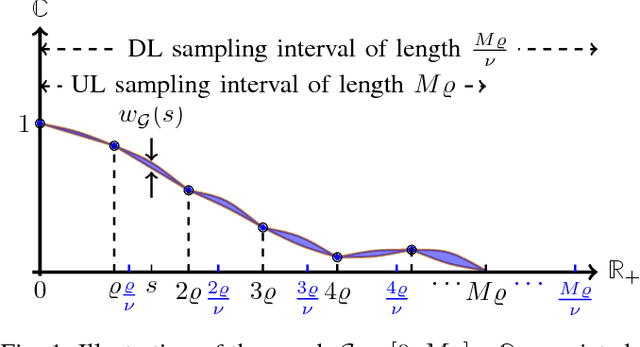
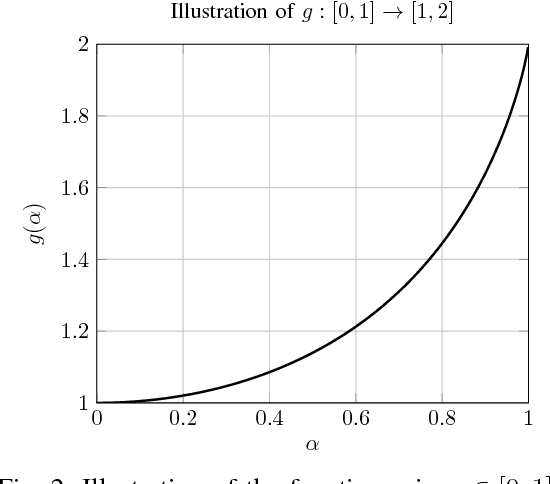
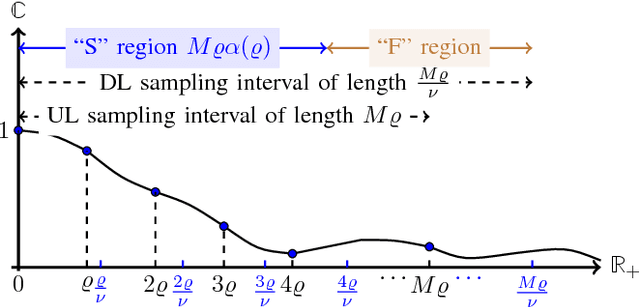
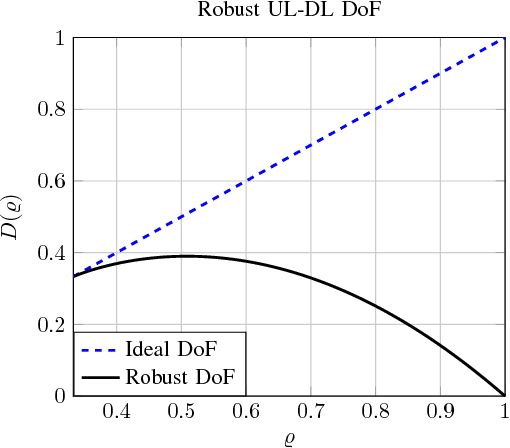
In this paper, we study the problem of multi-band (frequency-variant) covariance interpolation with a particular emphasis towards massive MIMO applications. In a massive MIMO system, the communication between each BS with $M \gg 1$ antennas and each single-antenna user occurs through a collection of scatterers in the environment, where the channel vector of each user at BS antennas consists in a weighted linear combination of the array responses of the scatterers, where each scatterer has its own angle of arrival (AoA) and complex channel gain. The array response at a given AoA depends on the wavelength of the incoming planar wave and is naturally frequency dependent. This results in a frequency-dependent distortion where the second order statistics, i.e., the covariance matrix, of the channel vectors varies with frequency. In this paper, we show that although this effect is generally negligible for a small number of antennas $M$, it results in a considerable distortion of the covariance matrix and especially its dominant signal subspace in the massive MIMO regime where $M \to \infty$, and can generally incur a serious degradation of the performance especially in frequency division duplexing (FDD) massive MIMO systems where the uplink (UL) and the downlink (DL) communication occur over different frequency bands. We propose a novel UL-DL covariance interpolation technique that is able to recover the covariance matrix in the DL from an estimate of the covariance matrix in the UL under a mild reciprocity condition on the angular power spread function (PSF) of the users. We analyze the performance of our proposed scheme mathematically and prove its robustness under a sufficiently large spatial oversampling of the array. We also propose several simple off-the-shelf algorithms for UL-DL covariance interpolation and evaluate their performance via numerical simulations.

Signal Recovery from Unlabeled Samples

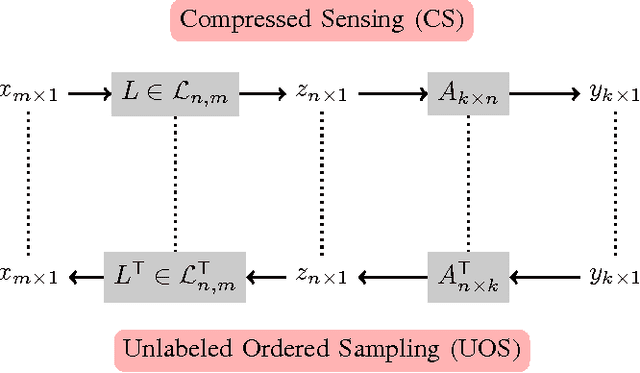
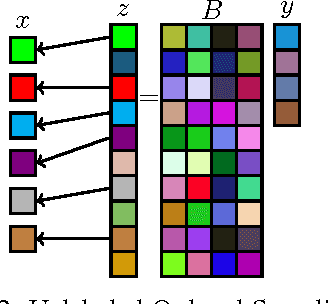
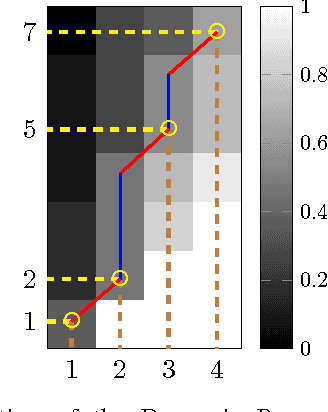
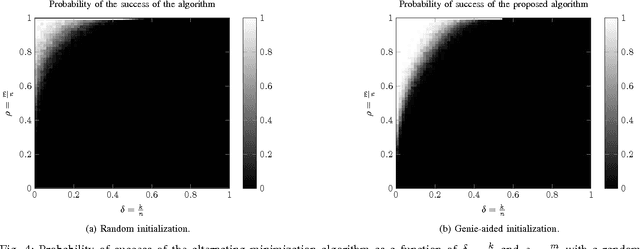
In this paper, we study the recovery of a signal from a set of noisy linear projections (measurements), when such projections are unlabeled, that is, the correspondence between the measurements and the set of projection vectors (i.e., the rows of the measurement matrix) is not known a priori. We consider a special case of unlabeled sensing referred to as Unlabeled Ordered Sampling (UOS) where the ordering of the measurements is preserved. We identify a natural duality between this problem and classical Compressed Sensing (CS), where we show that the unknown support (location of nonzero elements) of a sparse signal in CS corresponds to the unknown indices of the measurements in UOS. While in CS it is possible to recover a sparse signal from an under-determined set of linear equations (less equations than the signal dimension), successful recovery in UOS requires taking more samples than the dimension of the signal. Motivated by this duality, we develop a Restricted Isometry Property (RIP) similar to that in CS. We also design a low-complexity Alternating Minimization algorithm that achieves a stable signal recovery under the established RIP. We analyze our proposed algorithm for different signal dimensions and number of measurements theoretically and investigate its performance empirically via simulations. The results are reminiscent of phase-transition similar to that occurring in CS.

Compressive Estimation of a Stochastic Process with Unknown Autocorrelation Function

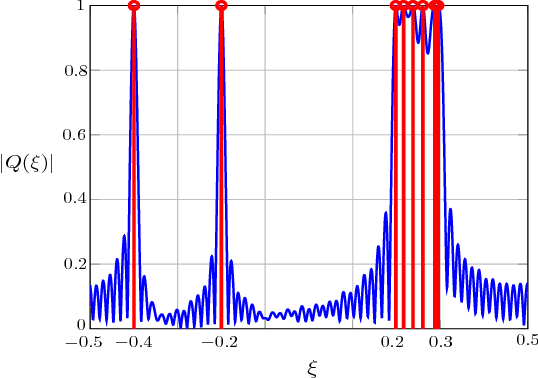
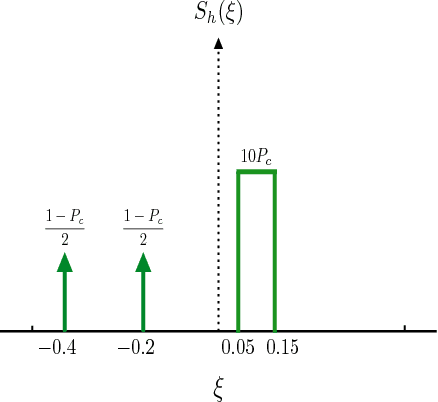
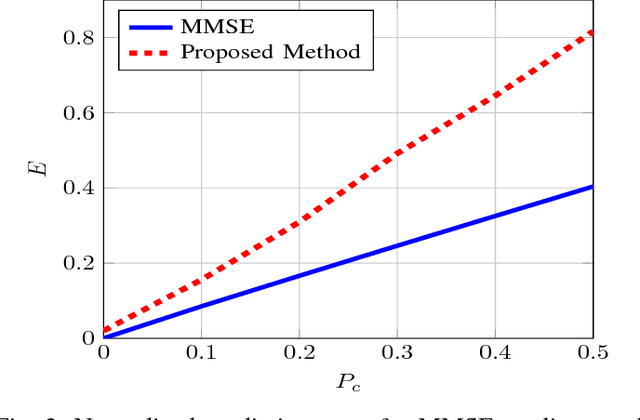
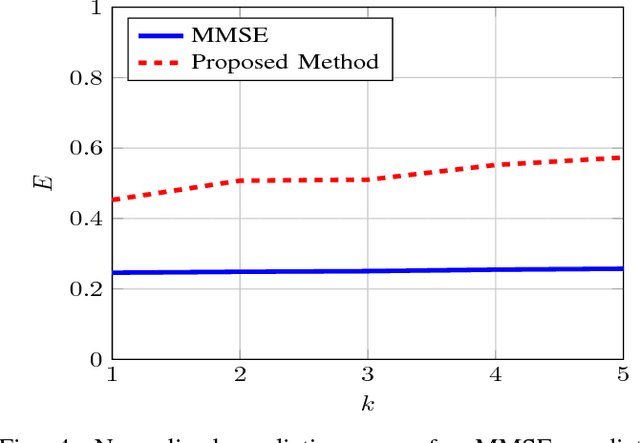
In this paper, we study the prediction of a circularly symmetric zero-mean stationary Gaussian process from a window of observations consisting of finitely many samples. This is a prevalent problem in a wide range of applications in communication theory and signal processing. Due to stationarity, when the autocorrelation function or equivalently the power spectral density (PSD) of the process is available, the Minimum Mean Squared Error (MMSE) predictor is readily obtained. In particular, it is given by a linear operator that depends on autocorrelation of the process as well as the noise power in the observed samples. The prediction becomes, however, quite challenging when the PSD of the process is unknown. In this paper, we propose a blind predictor that does not require the a priori knowledge of the PSD of the process and compare its performance with that of an MMSE predictor that has a full knowledge of the PSD. To design such a blind predictor, we use the random spectral representation of a stationary Gaussian process. We apply the well-known atomic-norm minimization technique to the observed samples to obtain a discrete quantization of the underlying random spectrum, which we use to predict the process. Our simulation results show that this estimator has a good performance comparable with that of the MMSE estimator.

Channel Vector Subspace Estimation from Low-Dimensional Projections

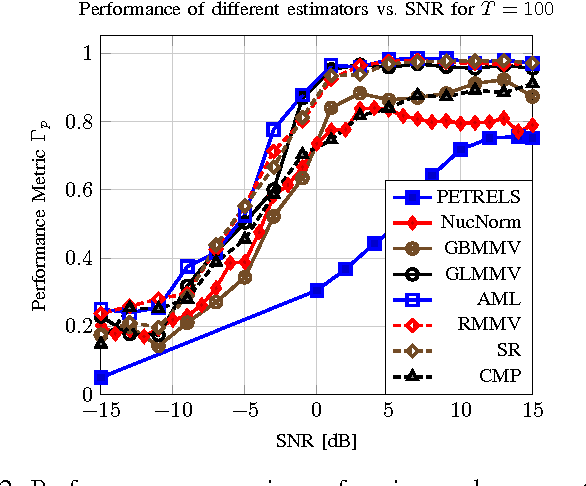
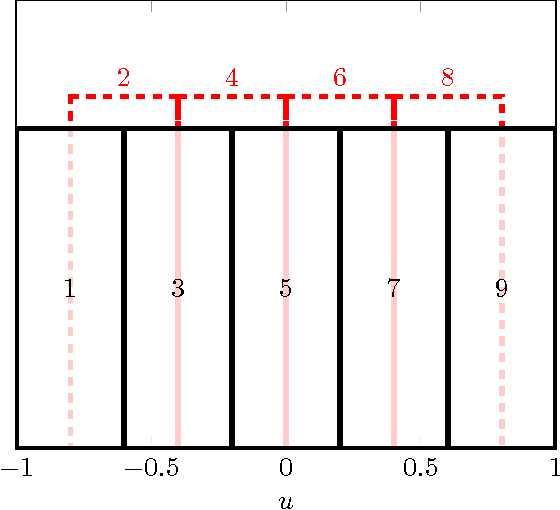
Massive MIMO is a variant of multiuser MIMO where the number of base-station antennas $M$ is very large (typically 100), and generally much larger than the number of spatially multiplexed data streams (typically 10). Unfortunately, the front-end A/D conversion necessary to drive hundreds of antennas, with a signal bandwidth of the order of 10 to 100 MHz, requires very large sampling bit-rate and power consumption. In order to reduce such implementation requirements, Hybrid Digital-Analog architectures have been proposed. In particular, our work in this paper is motivated by one of such schemes named Joint Spatial Division and Multiplexing (JSDM), where the downlink precoder (resp., uplink linear receiver) is split into the product of a baseband linear projection (digital) and an RF reconfigurable beamforming network (analog), such that only a reduced number $m \ll M$ of A/D converters and RF modulation/demodulation chains is needed. In JSDM, users are grouped according to the similarity of their channel dominant subspaces, and these groups are separated by the analog beamforming stage, where the multiplexing gain in each group is achieved using the digital precoder. Therefore, it is apparent that extracting the channel subspace information of the $M$-dim channel vectors from snapshots of $m$-dim projections, with $m \ll M$, plays a fundamental role in JSDM implementation. In this paper, we develop novel efficient algorithms that require sampling only $m = O(2\sqrt{M})$ specific array elements according to a coprime sampling scheme, and for a given $p \ll M$, return a $p$-dim beamformer that has a performance comparable with the best p-dim beamformer that can be designed from the full knowledge of the exact channel covariance matrix. We assess the performance of our proposed estimators both analytically and empirically via numerical simulations.

Multi Terminal Probabilistic Compressed Sensing

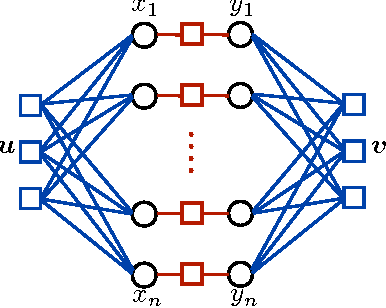
In this paper, the `Approximate Message Passing' (AMP) algorithm, initially developed for compressed sensing of signals under i.i.d. Gaussian measurement matrices, has been extended to a multi-terminal setting (MAMP algorithm). It has been shown that similar to its single terminal counterpart, the behavior of MAMP algorithm is fully characterized by a `State Evolution' (SE) equation for large block-lengths. This equation has been used to obtain the rate-distortion curve of a multi-terminal memoryless source. It is observed that by spatially coupling the measurement matrices, the rate-distortion curve of MAMP algorithm undergoes a phase transition, where the measurement rate region corresponding to a low distortion (approximately zero distortion) regime is fully characterized by the joint and conditional Renyi information dimension (RID) of the multi-terminal source. This measurement rate region is very similar to the rate region of the Slepian-Wolf distributed source coding problem where the RID plays a role similar to the discrete entropy. Simulations have been done to investigate the empirical behavior of MAMP algorithm. It is observed that simulation results match very well with predictions of SE equation for reasonably large block-lengths.

A Fast Hadamard Transform for Signals with Sub-linear Sparsity in the Transform Domain

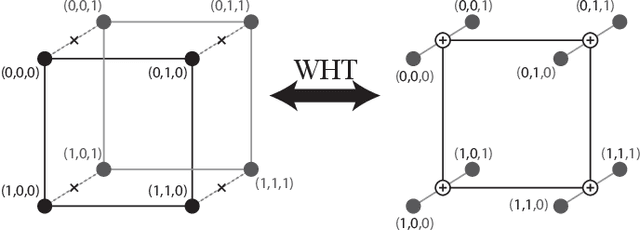
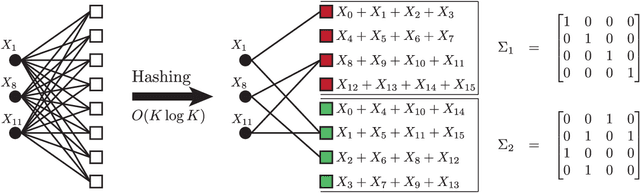
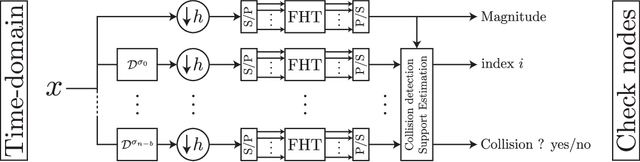
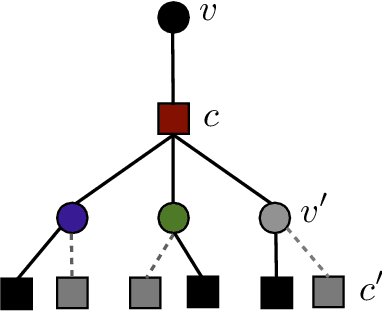
A new iterative low complexity algorithm has been presented for computing the Walsh-Hadamard transform (WHT) of an $N$ dimensional signal with a $K$-sparse WHT, where $N$ is a power of two and $K = O(N^\alpha)$, scales sub-linearly in $N$ for some $0 < \alpha < 1$. Assuming a random support model for the non-zero transform domain components, the algorithm reconstructs the WHT of the signal with a sample complexity $O(K \log_2(\frac{N}{K}))$, a computational complexity $O(K\log_2(K)\log_2(\frac{N}{K}))$ and with a very high probability asymptotically tending to 1. The approach is based on the subsampling (aliasing) property of the WHT, where by a carefully designed subsampling of the time domain signal, one can induce a suitable aliasing pattern in the transform domain. By treating the aliasing patterns as parity-check constraints and borrowing ideas from erasure correcting sparse-graph codes, the recovery of the non-zero spectral values has been formulated as a belief propagation (BP) algorithm (peeling decoding) over a sparse-graph code for the binary erasure channel (BEC). Tools from coding theory are used to analyze the asymptotic performance of the algorithm in the very sparse ($\alpha\in(0,\frac{1}{3}]$) and the less sparse ($\alpha\in(\frac{1}{3},1)$) regime.