Multiple Measurement Vectors Problem: A Decoupling Property and its Applications

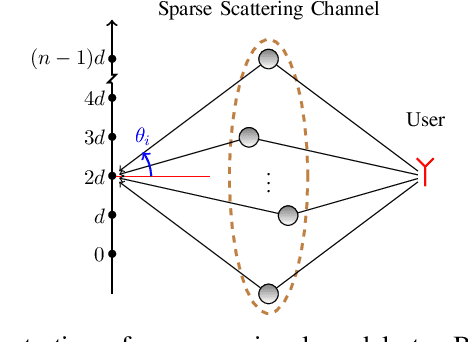
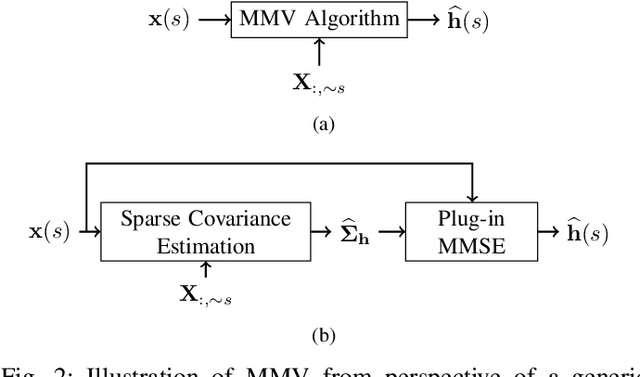
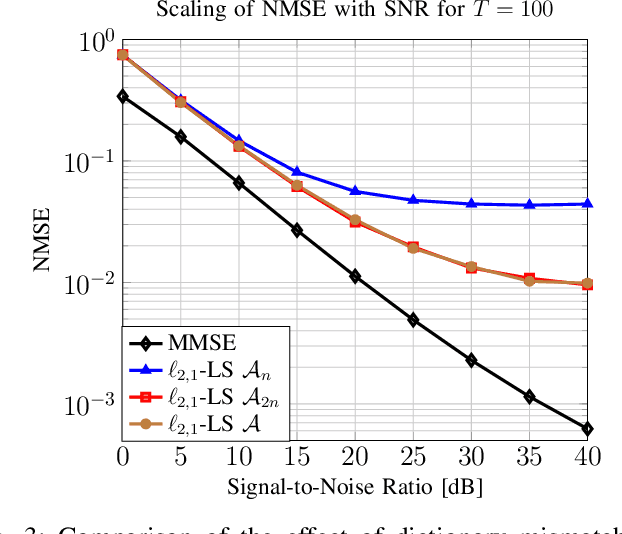
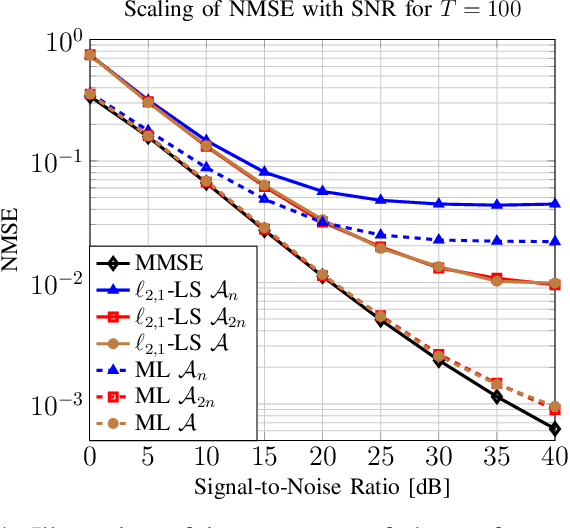
Efficient and reliable estimation in many signal processing problems encountered in applications requires adopting sparsity prior in a suitable basis on the signals and using techniques from compressed sensing (CS). In this paper, we study a CS problem known as Multiple Measurement Vectors (MMV) problem, which arises in joint estimation of multiple signal realizations when the signal samples have a common (joint) support over a fixed known dictionary. Although there is a vast literature on the analysis of MMV, it is not yet fully known how the number of signal samples and their statistical correlations affects the performance of the joint estimation in MMV. Moreover, in many instances of MMV the underlying sparsifying dictionary may not be precisely known, and it is still an open problem to quantify how the dictionary mismatch may affect the estimation performance. In this paper, we focus on $\ell_{2,1}$-norm regularized least squares ($\ell_{2,1}$-LS) as a well-known and widely-used MMV algorithm in the literature. We prove an interesting decoupling property for $\ell_{2,1}$-LS, where we show that it can be decomposed into two phases: i) use all the signal samples to estimate the signal covariance matrix (coupled phase), ii) plug in the resulting covariance estimate as the true covariance matrix into the Minimum Mean Squared Error (MMSE) estimator to reconstruct each signal sample individually (decoupled phase). As a consequence of this decomposition, we are able to provide further insights on the performance of $\ell_{2,1}$-LS for MMV. In particular, we address how the signal correlations and dictionary mismatch affects its estimation performance. We also provide numerical simulations to validate our theoretical results.