Signal Recovery from Unlabeled Samples
Paper and Code
Sep 01, 2017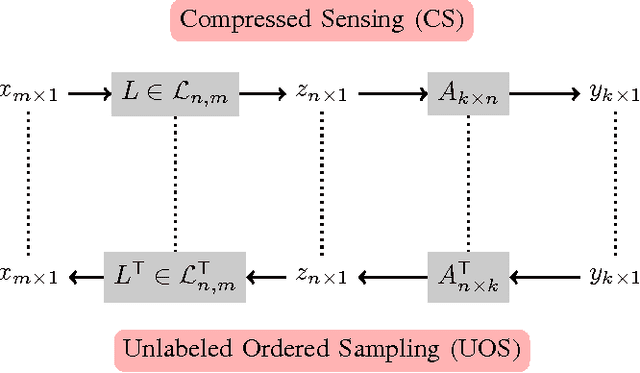
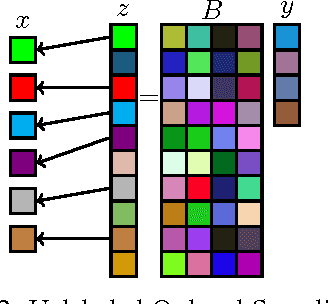
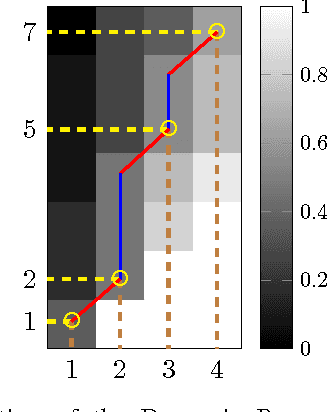
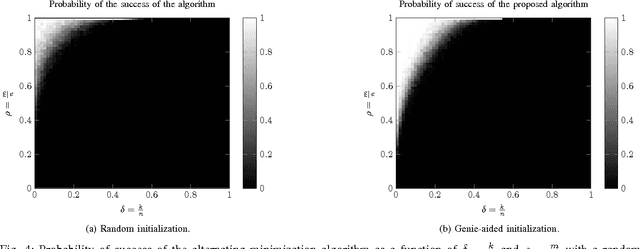
In this paper, we study the recovery of a signal from a set of noisy linear projections (measurements), when such projections are unlabeled, that is, the correspondence between the measurements and the set of projection vectors (i.e., the rows of the measurement matrix) is not known a priori. We consider a special case of unlabeled sensing referred to as Unlabeled Ordered Sampling (UOS) where the ordering of the measurements is preserved. We identify a natural duality between this problem and classical Compressed Sensing (CS), where we show that the unknown support (location of nonzero elements) of a sparse signal in CS corresponds to the unknown indices of the measurements in UOS. While in CS it is possible to recover a sparse signal from an under-determined set of linear equations (less equations than the signal dimension), successful recovery in UOS requires taking more samples than the dimension of the signal. Motivated by this duality, we develop a Restricted Isometry Property (RIP) similar to that in CS. We also design a low-complexity Alternating Minimization algorithm that achieves a stable signal recovery under the established RIP. We analyze our proposed algorithm for different signal dimensions and number of measurements theoretically and investigate its performance empirically via simulations. The results are reminiscent of phase-transition similar to that occurring in CS.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge