Channel Vector Subspace Estimation from Low-Dimensional Projections
Paper and Code
Jul 27, 2016
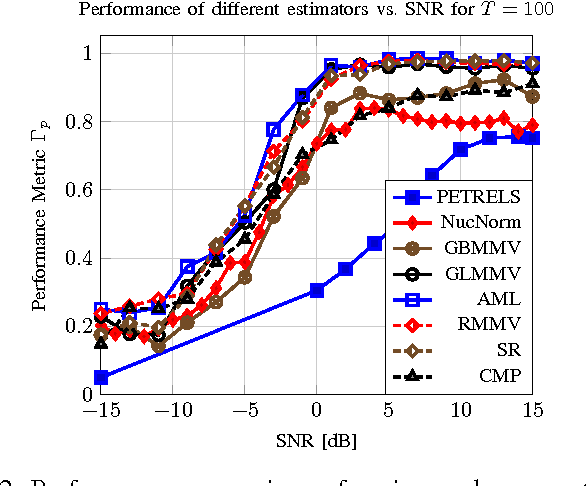
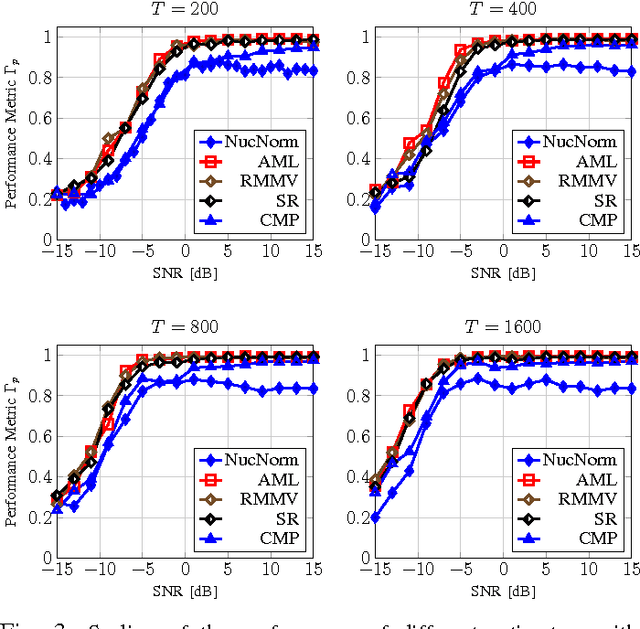
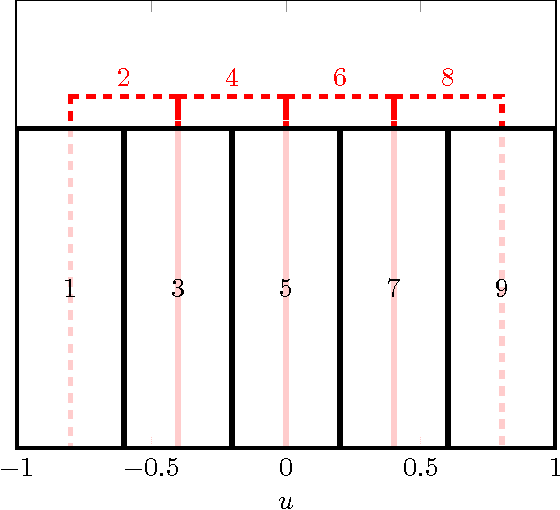
Massive MIMO is a variant of multiuser MIMO where the number of base-station antennas $M$ is very large (typically 100), and generally much larger than the number of spatially multiplexed data streams (typically 10). Unfortunately, the front-end A/D conversion necessary to drive hundreds of antennas, with a signal bandwidth of the order of 10 to 100 MHz, requires very large sampling bit-rate and power consumption. In order to reduce such implementation requirements, Hybrid Digital-Analog architectures have been proposed. In particular, our work in this paper is motivated by one of such schemes named Joint Spatial Division and Multiplexing (JSDM), where the downlink precoder (resp., uplink linear receiver) is split into the product of a baseband linear projection (digital) and an RF reconfigurable beamforming network (analog), such that only a reduced number $m \ll M$ of A/D converters and RF modulation/demodulation chains is needed. In JSDM, users are grouped according to the similarity of their channel dominant subspaces, and these groups are separated by the analog beamforming stage, where the multiplexing gain in each group is achieved using the digital precoder. Therefore, it is apparent that extracting the channel subspace information of the $M$-dim channel vectors from snapshots of $m$-dim projections, with $m \ll M$, plays a fundamental role in JSDM implementation. In this paper, we develop novel efficient algorithms that require sampling only $m = O(2\sqrt{M})$ specific array elements according to a coprime sampling scheme, and for a given $p \ll M$, return a $p$-dim beamformer that has a performance comparable with the best p-dim beamformer that can be designed from the full knowledge of the exact channel covariance matrix. We assess the performance of our proposed estimators both analytically and empirically via numerical simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge