Machine Learning for Geometrically-Consistent Angular Spread Function Estimation in Massive MIMO
Paper and Code
Oct 30, 2019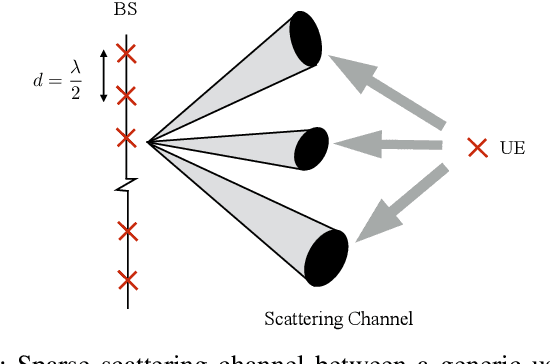
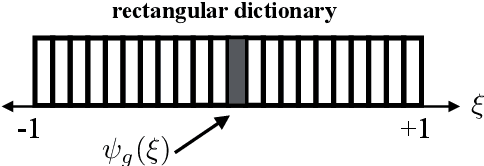
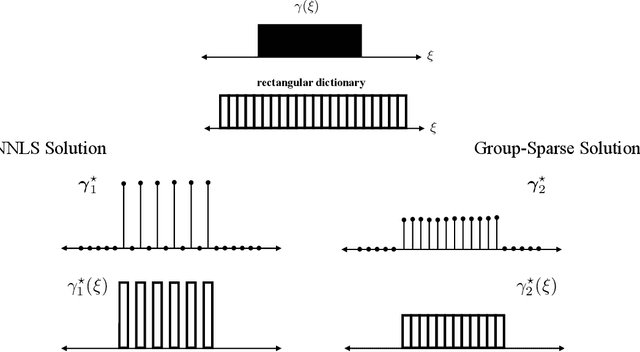
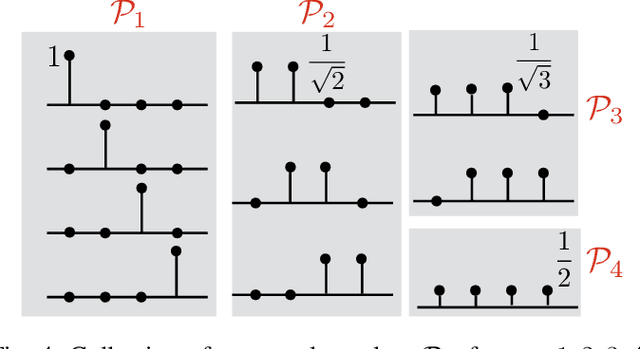
In the spatial channel models used in multi-antenna wireless communications, the propagation from a single-antenna transmitter (e.g., a user) to an M-antenna receiver (e.g., a Base Station) occurs through scattering clusters located in the far field of the receiving antenna array. The Angular Spread Function (ASF) of the corresponding M-dim channel vector describes the angular density of the received signal power at the array. The modern literature on massive MIMO has recognized that the knowledge of covariance matrix of user channel vectors is very useful for various applications such as hybrid digital analog beamforming, pilot decontamination, etc. Therefore, most literature has focused on the estimation of such channel covariance matrices. However, in some applications such as uplink-downlink covariance transformation (for FDD massive MIMO precoding) and channel sounding some form of ASF estimation is required either implicitly or explicitly. It turns out that while covariance estimation is well-known and well-conditioned, the ASF estimation is a much harder problem and is in general ill-posed. In this paper, we show that under additional geometrically-consistent group-sparsity structure on the ASF, which is prevalent in almost all wireless propagation scenarios, one is able to estimate ASF properly. We propose sparse dictionary-based algorithms that promote this group-sparsity structure via suitable regularizations. Since generally it is difficult to capture the notion of group-sparsity through proper regularization, we propose another algorithm based on Deep Neural Networks (DNNs) that learns this structure. We provide numerical simulations to assess the performance of our proposed algorithms. We also compare the results with that of other methods in the literature, where we re-frame those methods in the context of ASF estimation in massive MIMO.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge