Deep-Learning Aided Channel Training and Precoding in FDD Massive MIMO with Channel Statistics Knowledge

We propose a method for channel training and precoding in FDD massive MIMO based on deep neural networks (DNNs), exploiting Downlink (DL) channel covariance knowledge. The DNN is optimized to maximize the DL multi-user sum-rate, by producing a pre-beamforming matrix based on user channel covariances that maps the original channel vectors to effective channels. Measurements of these effective channels are received at the users via common pilot transmission and sent back to the base station (BS) through analog feedback without further processing. The BS estimates the effective channels from received feedback and constructs a linear precoder by concatenating the optimized pre-beamforming matrix with a zero-forcing precoder over the effective channels. We show that the proposed method yields significantly higher sum-rates than the state-of-the-art DNN-based channel training and precoding scheme, especially in scenarios with small pilot and feedback size relative to the channel coherence block length. Unlike many works in the literature, our proposition does not involve deployment of a DNN at the user side, which typically comes at a high computational cost and parameter-transmission overhead on the system, and is therefore considerably more practical.

Machine Learning for Geometrically-Consistent Angular Spread Function Estimation in Massive MIMO

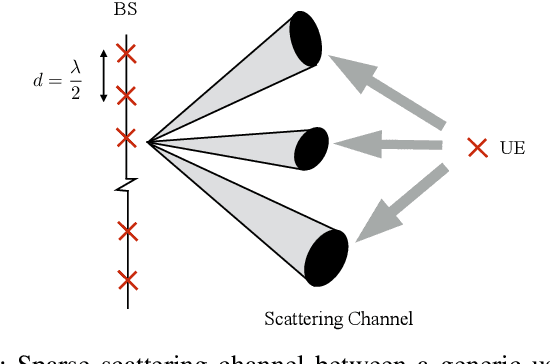
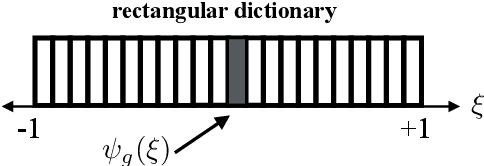
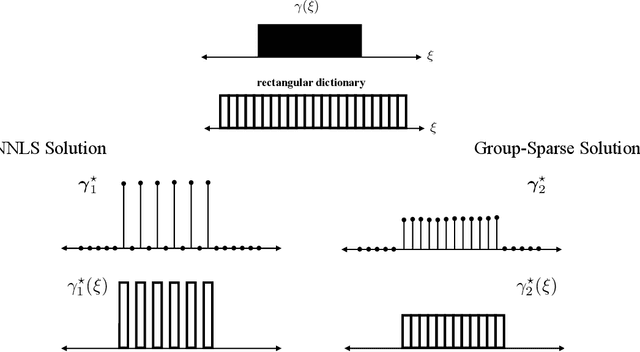
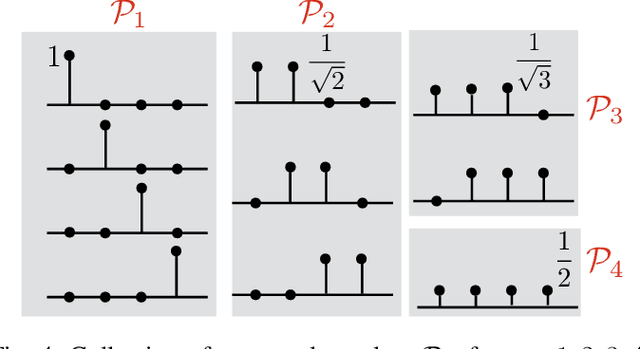
In the spatial channel models used in multi-antenna wireless communications, the propagation from a single-antenna transmitter (e.g., a user) to an M-antenna receiver (e.g., a Base Station) occurs through scattering clusters located in the far field of the receiving antenna array. The Angular Spread Function (ASF) of the corresponding M-dim channel vector describes the angular density of the received signal power at the array. The modern literature on massive MIMO has recognized that the knowledge of covariance matrix of user channel vectors is very useful for various applications such as hybrid digital analog beamforming, pilot decontamination, etc. Therefore, most literature has focused on the estimation of such channel covariance matrices. However, in some applications such as uplink-downlink covariance transformation (for FDD massive MIMO precoding) and channel sounding some form of ASF estimation is required either implicitly or explicitly. It turns out that while covariance estimation is well-known and well-conditioned, the ASF estimation is a much harder problem and is in general ill-posed. In this paper, we show that under additional geometrically-consistent group-sparsity structure on the ASF, which is prevalent in almost all wireless propagation scenarios, one is able to estimate ASF properly. We propose sparse dictionary-based algorithms that promote this group-sparsity structure via suitable regularizations. Since generally it is difficult to capture the notion of group-sparsity through proper regularization, we propose another algorithm based on Deep Neural Networks (DNNs) that learns this structure. We provide numerical simulations to assess the performance of our proposed algorithms. We also compare the results with that of other methods in the literature, where we re-frame those methods in the context of ASF estimation in massive MIMO.

Multi-Band Covariance Interpolation with Applications in Massive MIMO

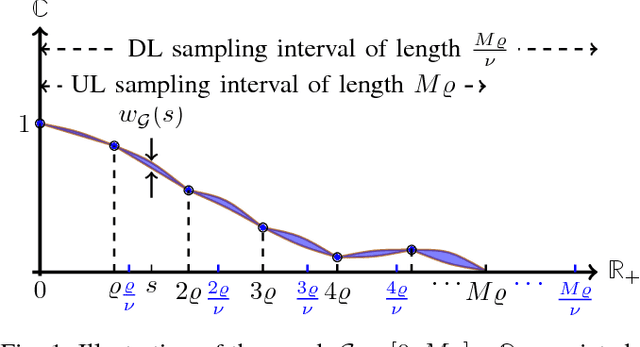
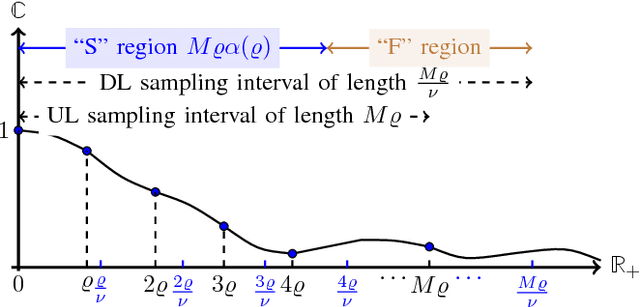
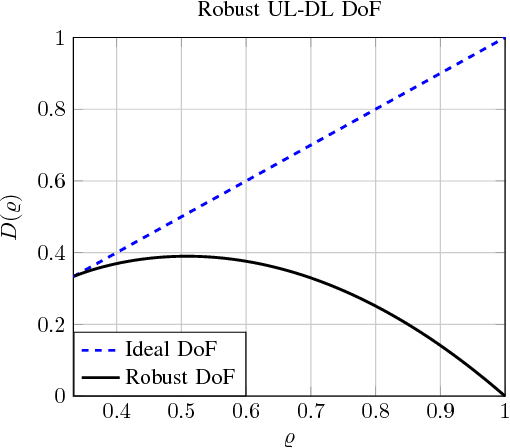
In this paper, we study the problem of multi-band (frequency-variant) covariance interpolation with a particular emphasis towards massive MIMO applications. In a massive MIMO system, the communication between each BS with $M \gg 1$ antennas and each single-antenna user occurs through a collection of scatterers in the environment, where the channel vector of each user at BS antennas consists in a weighted linear combination of the array responses of the scatterers, where each scatterer has its own angle of arrival (AoA) and complex channel gain. The array response at a given AoA depends on the wavelength of the incoming planar wave and is naturally frequency dependent. This results in a frequency-dependent distortion where the second order statistics, i.e., the covariance matrix, of the channel vectors varies with frequency. In this paper, we show that although this effect is generally negligible for a small number of antennas $M$, it results in a considerable distortion of the covariance matrix and especially its dominant signal subspace in the massive MIMO regime where $M \to \infty$, and can generally incur a serious degradation of the performance especially in frequency division duplexing (FDD) massive MIMO systems where the uplink (UL) and the downlink (DL) communication occur over different frequency bands. We propose a novel UL-DL covariance interpolation technique that is able to recover the covariance matrix in the DL from an estimate of the covariance matrix in the UL under a mild reciprocity condition on the angular power spread function (PSF) of the users. We analyze the performance of our proposed scheme mathematically and prove its robustness under a sufficiently large spatial oversampling of the array. We also propose several simple off-the-shelf algorithms for UL-DL covariance interpolation and evaluate their performance via numerical simulations.

Compressive Estimation of a Stochastic Process with Unknown Autocorrelation Function

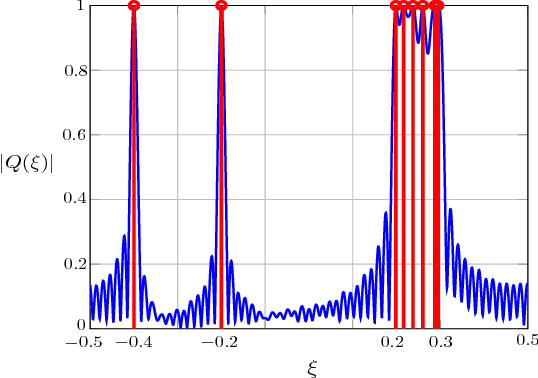
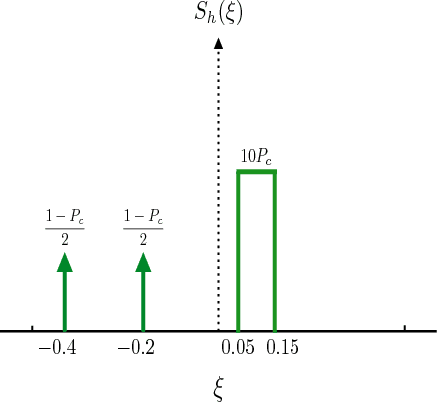
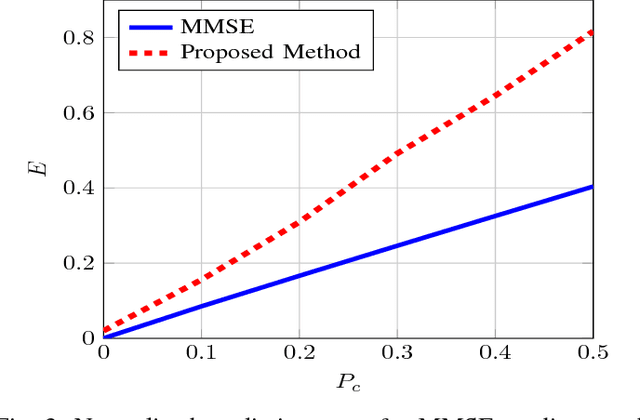
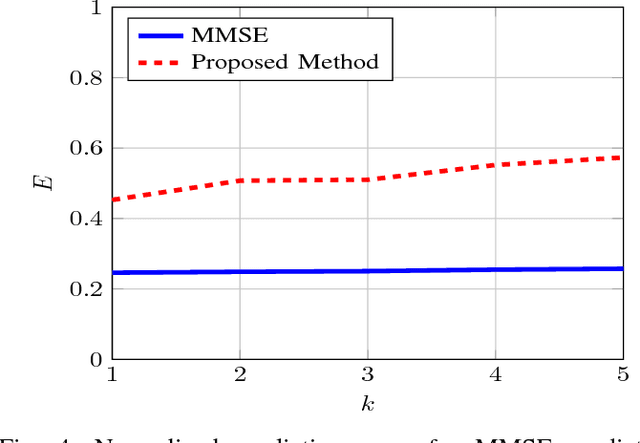
In this paper, we study the prediction of a circularly symmetric zero-mean stationary Gaussian process from a window of observations consisting of finitely many samples. This is a prevalent problem in a wide range of applications in communication theory and signal processing. Due to stationarity, when the autocorrelation function or equivalently the power spectral density (PSD) of the process is available, the Minimum Mean Squared Error (MMSE) predictor is readily obtained. In particular, it is given by a linear operator that depends on autocorrelation of the process as well as the noise power in the observed samples. The prediction becomes, however, quite challenging when the PSD of the process is unknown. In this paper, we propose a blind predictor that does not require the a priori knowledge of the PSD of the process and compare its performance with that of an MMSE predictor that has a full knowledge of the PSD. To design such a blind predictor, we use the random spectral representation of a stationary Gaussian process. We apply the well-known atomic-norm minimization technique to the observed samples to obtain a discrete quantization of the underlying random spectrum, which we use to predict the process. Our simulation results show that this estimator has a good performance comparable with that of the MMSE estimator.