Multi-Band Covariance Interpolation with Applications in Massive MIMO
Paper and Code
Jan 11, 2018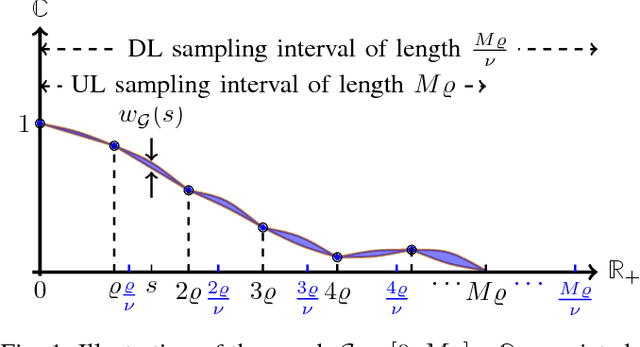
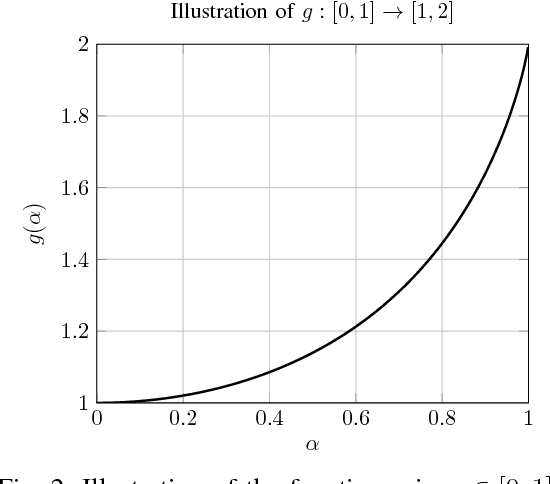
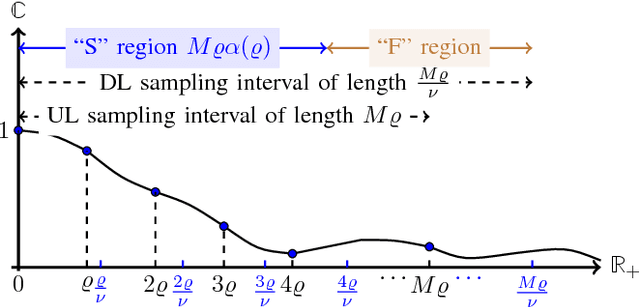
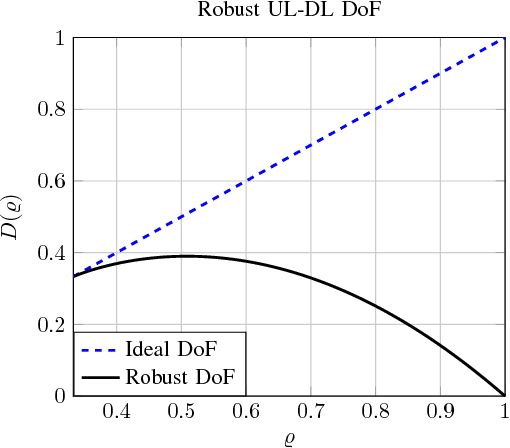
In this paper, we study the problem of multi-band (frequency-variant) covariance interpolation with a particular emphasis towards massive MIMO applications. In a massive MIMO system, the communication between each BS with $M \gg 1$ antennas and each single-antenna user occurs through a collection of scatterers in the environment, where the channel vector of each user at BS antennas consists in a weighted linear combination of the array responses of the scatterers, where each scatterer has its own angle of arrival (AoA) and complex channel gain. The array response at a given AoA depends on the wavelength of the incoming planar wave and is naturally frequency dependent. This results in a frequency-dependent distortion where the second order statistics, i.e., the covariance matrix, of the channel vectors varies with frequency. In this paper, we show that although this effect is generally negligible for a small number of antennas $M$, it results in a considerable distortion of the covariance matrix and especially its dominant signal subspace in the massive MIMO regime where $M \to \infty$, and can generally incur a serious degradation of the performance especially in frequency division duplexing (FDD) massive MIMO systems where the uplink (UL) and the downlink (DL) communication occur over different frequency bands. We propose a novel UL-DL covariance interpolation technique that is able to recover the covariance matrix in the DL from an estimate of the covariance matrix in the UL under a mild reciprocity condition on the angular power spread function (PSF) of the users. We analyze the performance of our proposed scheme mathematically and prove its robustness under a sufficiently large spatial oversampling of the array. We also propose several simple off-the-shelf algorithms for UL-DL covariance interpolation and evaluate their performance via numerical simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge