A Fast Hadamard Transform for Signals with Sub-linear Sparsity in the Transform Domain
Paper and Code
Dec 29, 2013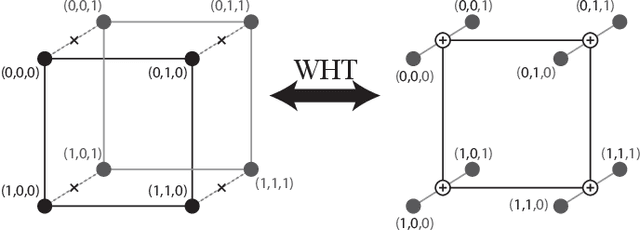
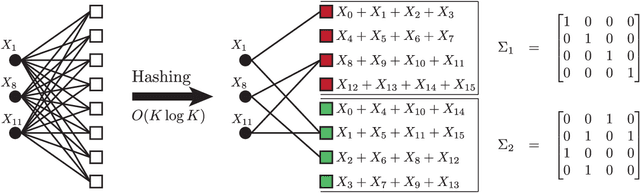
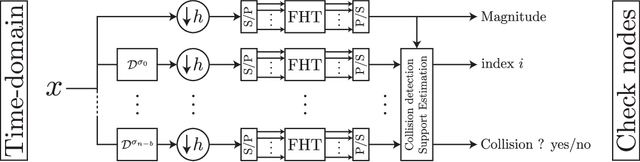
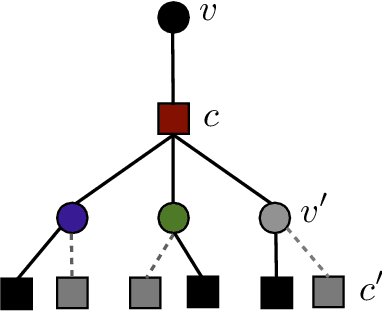
A new iterative low complexity algorithm has been presented for computing the Walsh-Hadamard transform (WHT) of an $N$ dimensional signal with a $K$-sparse WHT, where $N$ is a power of two and $K = O(N^\alpha)$, scales sub-linearly in $N$ for some $0 < \alpha < 1$. Assuming a random support model for the non-zero transform domain components, the algorithm reconstructs the WHT of the signal with a sample complexity $O(K \log_2(\frac{N}{K}))$, a computational complexity $O(K\log_2(K)\log_2(\frac{N}{K}))$ and with a very high probability asymptotically tending to 1. The approach is based on the subsampling (aliasing) property of the WHT, where by a carefully designed subsampling of the time domain signal, one can induce a suitable aliasing pattern in the transform domain. By treating the aliasing patterns as parity-check constraints and borrowing ideas from erasure correcting sparse-graph codes, the recovery of the non-zero spectral values has been formulated as a belief propagation (BP) algorithm (peeling decoding) over a sparse-graph code for the binary erasure channel (BEC). Tools from coding theory are used to analyze the asymptotic performance of the algorithm in the very sparse ($\alpha\in(0,\frac{1}{3}]$) and the less sparse ($\alpha\in(\frac{1}{3},1)$) regime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge