Taming Diffusion Prior for Image Super-Resolution with Domain Shift SDEs

Diffusion-based image super-resolution (SR) models have attracted substantial interest due to their powerful image restoration capabilities. However, prevailing diffusion models often struggle to strike an optimal balance between efficiency and performance. Typically, they either neglect to exploit the potential of existing extensive pretrained models, limiting their generative capacity, or they necessitate a dozens of forward passes starting from random noises, compromising inference efficiency. In this paper, we present DoSSR, a Domain Shift diffusion-based SR model that capitalizes on the generative powers of pretrained diffusion models while significantly enhancing efficiency by initiating the diffusion process with low-resolution (LR) images. At the core of our approach is a domain shift equation that integrates seamlessly with existing diffusion models. This integration not only improves the use of diffusion prior but also boosts inference efficiency. Moreover, we advance our method by transitioning the discrete shift process to a continuous formulation, termed as DoS-SDEs. This advancement leads to the fast and customized solvers that further enhance sampling efficiency. Empirical results demonstrate that our proposed method achieves state-of-the-art performance on synthetic and real-world datasets, while notably requiring only 5 sampling steps. Compared to previous diffusion prior based methods, our approach achieves a remarkable speedup of 5-7 times, demonstrating its superior efficiency. Code: https://github.com/QinpengCui/DoSSR.

Pose Magic: Efficient and Temporally Consistent Human Pose Estimation with a Hybrid Mamba-GCN Network

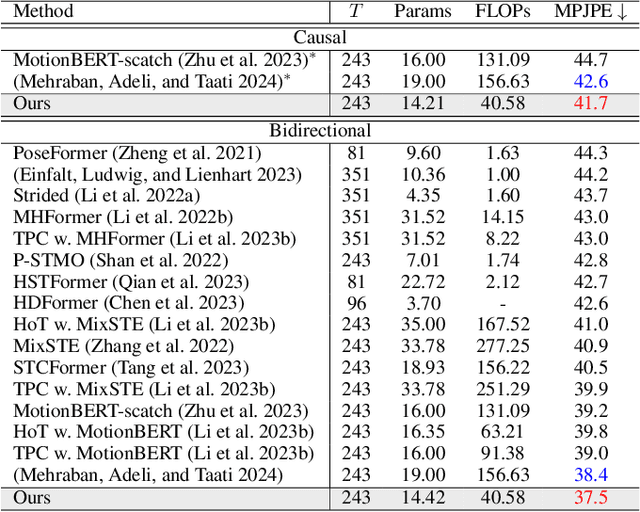
Current state-of-the-art (SOTA) methods in 3D Human Pose Estimation (HPE) are primarily based on Transformers. However, existing Transformer-based 3D HPE backbones often encounter a trade-off between accuracy and computational efficiency. To resolve the above dilemma, in this work, we leverage recent advances in state space models and utilize Mamba for high-quality and efficient long-range modeling. Nonetheless, Mamba still faces challenges in precisely exploiting local dependencies between joints. To address these issues, we propose a new attention-free hybrid spatiotemporal architecture named Hybrid Mamba-GCN (Pose Magic). This architecture introduces local enhancement with GCN by capturing relationships between neighboring joints, thus producing new representations to complement Mamba's outputs. By adaptively fusing representations from Mamba and GCN, Pose Magic demonstrates superior capability in learning the underlying 3D structure. To meet the requirements of real-time inference, we also provide a fully causal version. Extensive experiments show that Pose Magic achieves new SOTA results ($\downarrow 0.9 mm$) while saving $74.1\%$ FLOPs. In addition, Pose Magic exhibits optimal motion consistency and the ability to generalize to unseen sequence lengths.

Elucidating the solution space of extended reverse-time SDE for diffusion models

Diffusion models (DMs) demonstrate potent image generation capabilities in various generative modeling tasks. Nevertheless, their primary limitation lies in slow sampling speed, requiring hundreds or thousands of sequential function evaluations through large neural networks to generate high-quality images. Sampling from DMs can be seen alternatively as solving corresponding stochastic differential equations (SDEs) or ordinary differential equations (ODEs). In this work, we formulate the sampling process as an extended reverse-time SDE (ER SDE), unifying prior explorations into ODEs and SDEs. Leveraging the semi-linear structure of ER SDE solutions, we offer exact solutions and arbitrarily high-order approximate solutions for VP SDE and VE SDE, respectively. Based on the solution space of the ER SDE, we yield mathematical insights elucidating the superior performance of ODE solvers over SDE solvers in terms of fast sampling. Additionally, we unveil that VP SDE solvers stand on par with their VE SDE counterparts. Finally, we devise fast and training-free samplers, ER-SDE-Solvers, achieving state-of-the-art performance across all stochastic samplers. Experimental results demonstrate achieving 3.45 FID in 20 function evaluations and 2.24 FID in 50 function evaluations on the ImageNet $64\times64$ dataset.