A review of cuspidal serial and parallel manipulators

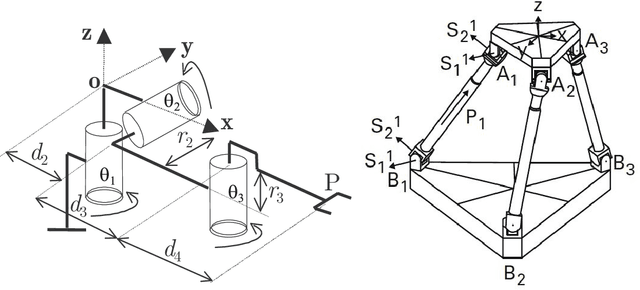
Cuspidal robots can move from one inverse or direct kinematic solution to another without ever passing through a singularity. These robots have remained unknown because almost all industrial robots do not have this feature. However, in fact, industrial robots are the exceptions. Some robots appeared recently in the industrial market can be shown to be cuspidal but, surprisingly, almost nobody knows it and robot users meet difficulties in planning trajectories with these robots. This paper proposes a review on the fundamental and application aspects of cuspidal robots. It addresses the important issues raised by these robots for the design and planning of trajectories. The identification of all cuspidal robots is still an open issue. This paper recalls in details the case of serial robots with three joints but it also addresses robots with more complex architectures such as 6-revolute-jointed robot and parallel robots. We hope that this paper will help disseminate more widely knowledge on cuspidal robots.

Deciding cuspidality of manipulators through computer algebra and algorithms in real algebraic geometry

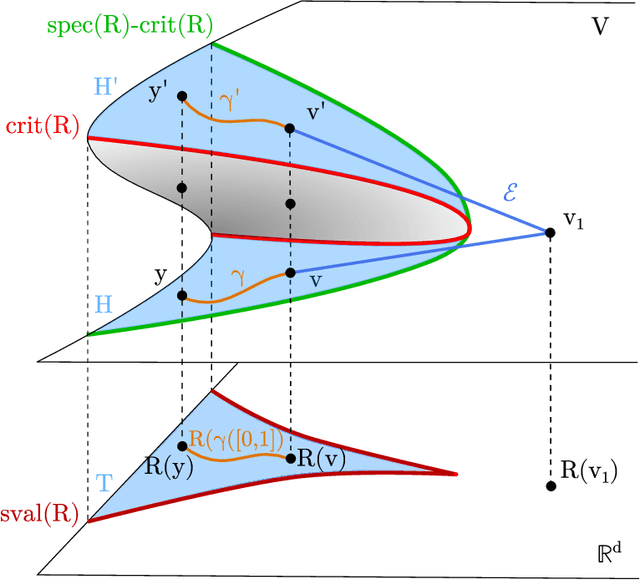
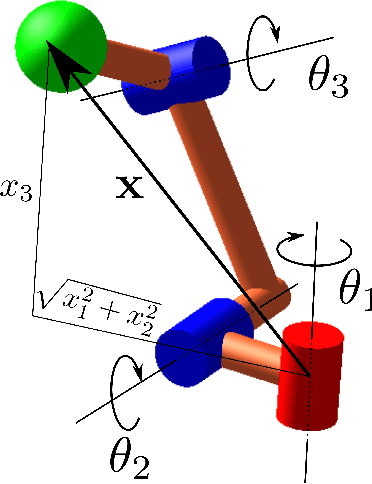
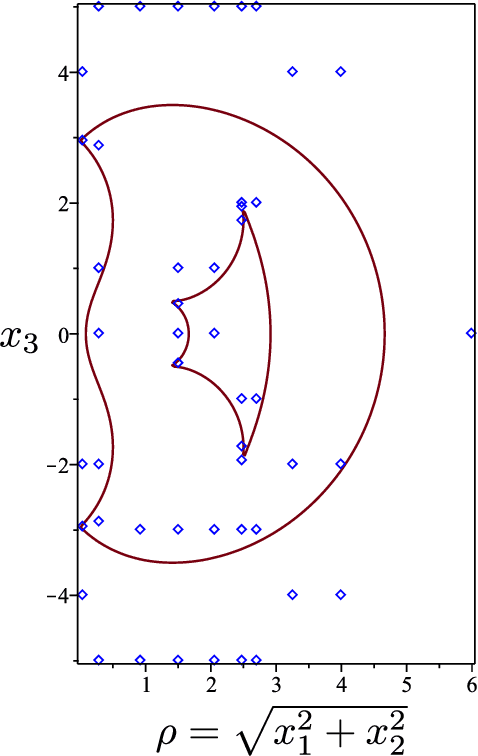
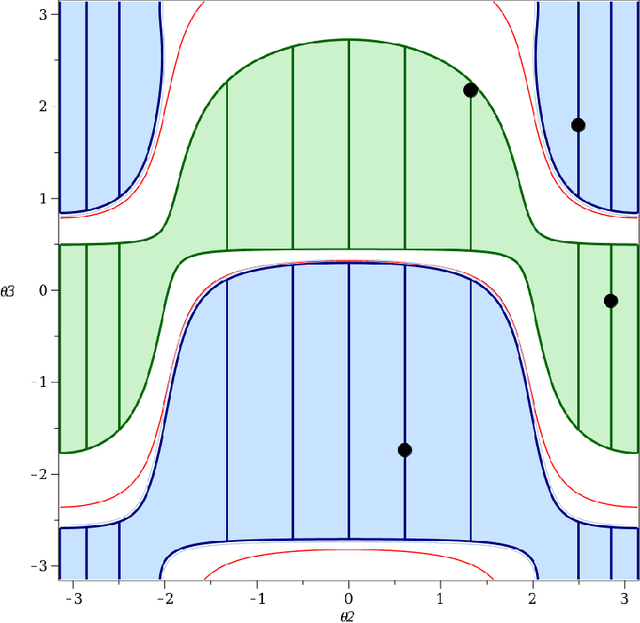
Cuspidal robots are robots with at least two inverse kinematic solutions that can be connected by a singularity-free path. Deciding the cuspidality of a generic 3R robots has been studied in the past, but extending the study to six-degree-of-freedom robots can be a challenging problem. Many robots can be modeled as a polynomial map together with a real algebraic set so that the notion of cuspidality can be extended to these data.In this paper we design an algorithm that, on input a polynomial map in $n$ indeterminates, and $s$ polynomials in the same indeterminates describing a real algebraic set of dimension $d$, decides the cuspidality of the restriction of the map to the real algebraic set under consideration. Moreover, if $D$ and $\tau$ are respectively the maximum degree and a bound on the bit size of the coefficients of the input polynomials, this algorithm runs in time log-linear in $\tau$ and polynomial in $((s+d)nD)^{O(n^2)}$.It relies on many high-level algorithms in computer algebra which use advanced methods on real algebraic sets and critical loci of polynomial maps. As far as we know, this is the first algorithm that tackles the cuspidality problem from a general point of view.

Necessary and sufficient condition for a generic 3R serial manipulator to be cuspidal

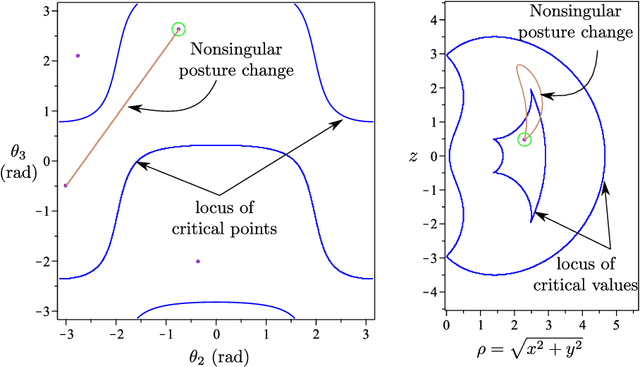
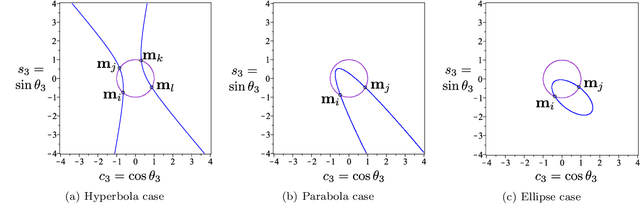
Cuspidal robots can travel from one inverse kinematic solution to another without meeting a singularity. The name cuspidal was coined based on the existence of a cusp point in the workspace of 3R serial robots. The existence of a cusp point was proved to be a necessary and sufficient condition for orthogonal robots to be cuspidal, but it was not possible to extend this condition to non-orthogonal robots. The goal of this paper is to prove that this condition stands for any generic 3R robot. This result would give the designer more flexibility. In the presented work, the geometrical interpretation of the inverse kinematics of 3R robots is revisited and important observations on the nonsingular change of posture are noted. The paper presents a theorem regarding the existence of reduced aspects in any generic 3R serial robot. Based on these observations and on this theorem, we prove that the existence of a cusp point is a necessary and sufficient condition for any 3R generic robot to be cuspidal.

Kinetostatic analysis and solution classification of a class of planar tensegrity mechanisms

Tensegrity mechanisms are composed of rigid and tensile parts that are in equilibrium. They are interesting alternative designs for some applications, such as modelling musculo-skeleton systems. Tensegrity mechanisms are more difficult to analyze than classical mechanisms as the static equilibrium conditions that must be satisfied generally result in complex equations. A class of planar one-degree-of-freedom tensegrity mechanisms with three linear springs is analyzed in detail for the sake of systematic solution classifications. The kinetostatic equations are derived and solved under several loading and geometric conditions. It is shown that these mechanisms exhibit up to six equilibrium configurations, of which one or two are stable, depending on the geometric and loading conditions. Discriminant varieties and cylindrical algebraic decomposition combined with Groebner base elimination are used to classify solutions as a function of the geometric, loading and actuator input parameters.

Cuspidal Robots

This chapter is dedicated to the so-called cuspidal robots, i.e. those robots that can move from one inverse geometric solution to another without meeting a singular confuguration. This feature was discovered quite recently and has then been fascinating a lot of researchers. After a brief history of cuspidal robots, the chapter provides the main features of cuspidal robots: explanation of the non-singular change of posture, uniqueness domains, regions of feasible paths, identification and classification of cuspidal robots. The chapter focuses on 3-R orthogonal serial robots. The case of 6-dof robots and parallel robots is discussed in the end of this chapter.

Hidden cusps

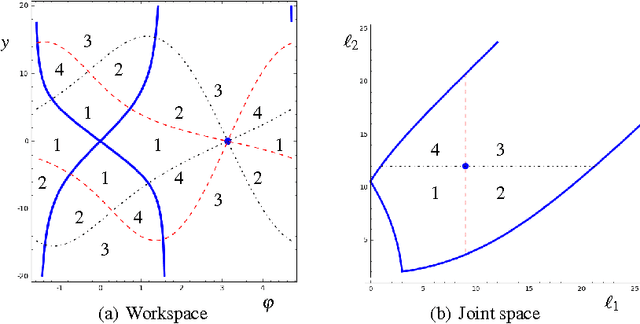
This paper investigates a situation pointed out in a recent paper, in which a non-singular change of assembly mode of a planar 2-RPR-PR parallel manipulator was realized by encircling a point of multiplicity 4. It is shown that this situation is, in fact, a non-generic one and gives rise to cusps under a small perturbation. Furthermore , we show that, for a large class of singularities of multiplicity 4, there are only two types of stable singularities occurring in a small perturbation: these two types are given by the complex square mapping and the quarto mapping. Incidentally , this paper confirms the fact that, generically, a local non-singular change of solution must be accomplished by encircling a cusp point.

Sensitivity Analysis of the Orthoglide, a 3-DOF Translational Parallel Kinematic Machine

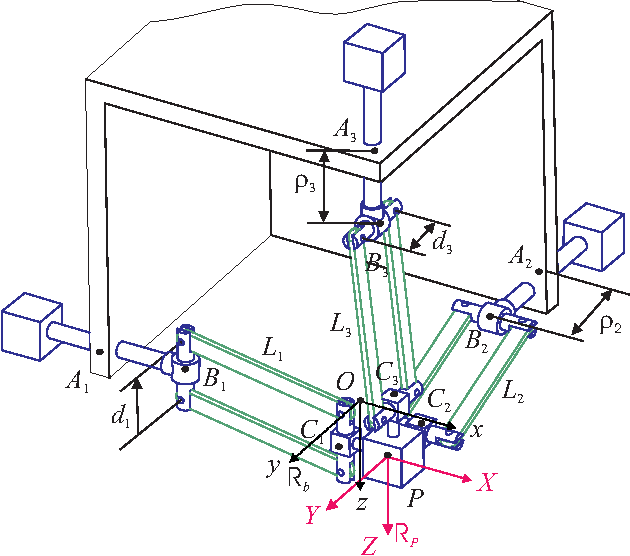
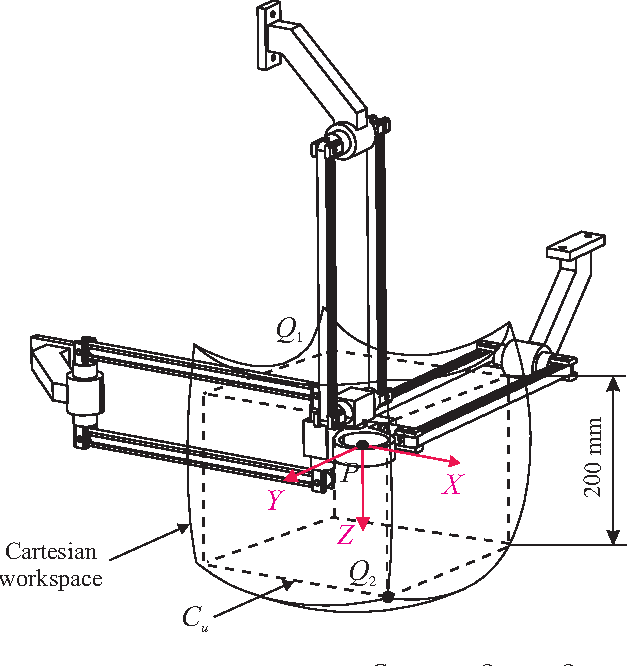
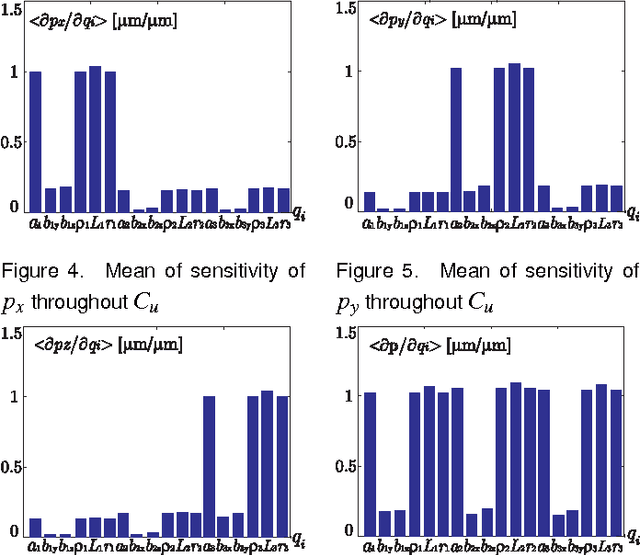
This paper presents a sensitivity analysis of the Orthoglide, a 3-DOF translational Parallel Kinematic Machine. Two complementary methods are developed to analyze its sensitivity to its dimensional and angular variations. First, a linkage kinematic analysis method is used to have a rough idea of the influence of the dimensional variations on the location of the end-effector. Besides, this method shows that variations in the design parameters of the same type from one leg to the other have the same influence on the end-effector. However, this method does not take into account the variations in the parallelograms. Thus, a differential vector method is used to study the influence of the dimensional and angular variations in the parts of the manipulator on the position and orientation of the end-effector, and particularly the influence of the variations in the parallelograms. It turns out that the kinematic isotropic configuration of the manipulator is the least sensitive one to its dimensional and angular variations. On the contrary, the closest configurations to its kinematic singular configurations are the most sensitive ones to geometrical variations.

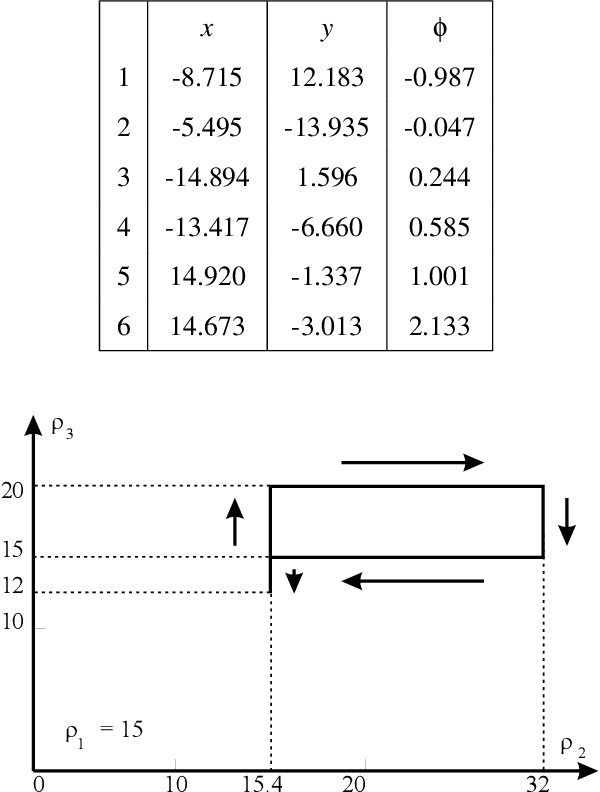
Cusp Points in the Parameter Space of Degenerate 3-RPR Planar Parallel Manipulators

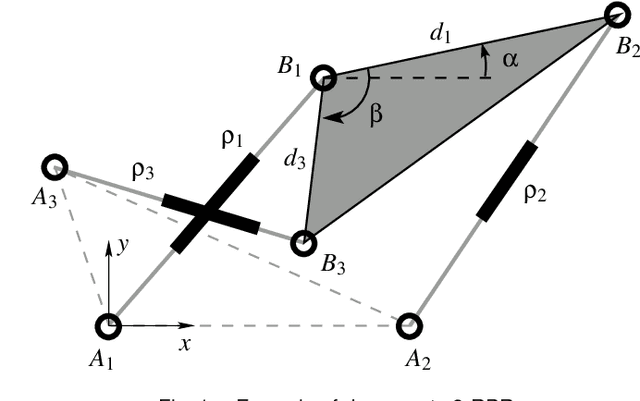
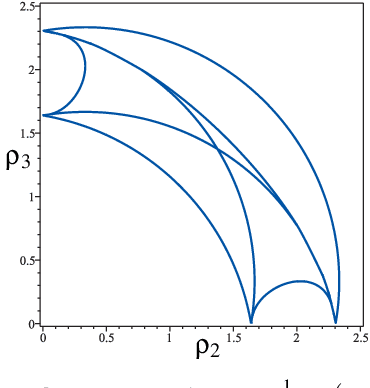
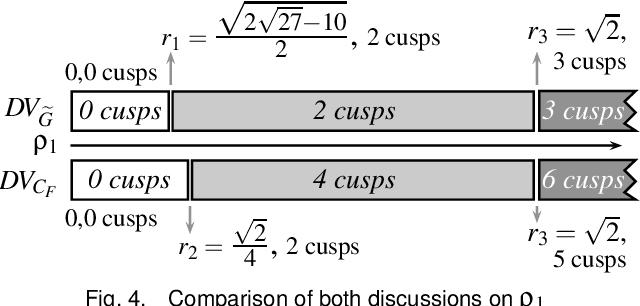
This paper investigates the conditions in the design parameter space for the existence and distribution of the cusp locus for planar parallel manipulators. Cusp points make possible non-singular assembly-mode changing motion, which increases the maximum singularity-free workspace. An accurate algorithm for the determination is proposed amending some imprecisions done by previous existing algorithms. This is combined with methods of Cylindric Algebraic Decomposition, Gr\"obner bases and Discriminant Varieties in order to partition the parameter space into cells with constant number of cusp points. These algorithms will allow us to classify a family of degenerate 3-RPR manipulators.

Solution regions in the parameter space of a 3-RRR decoupled robot for a prescribed workspace

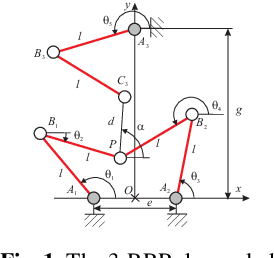
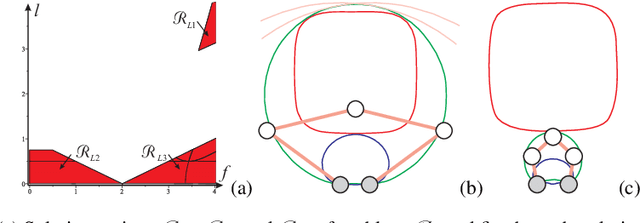
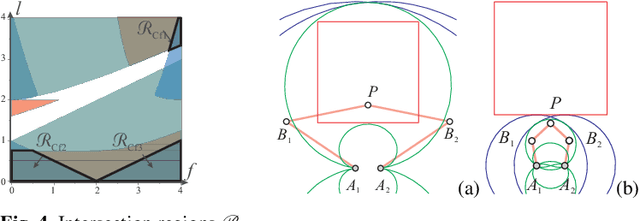
This paper proposes a new design method to determine the feasible set of parameters of translational or position/orientation decoupled parallel robots for a prescribed singularity-free workspace of regular shape. The suggested method uses Groebner bases to define the singularities and the cylindrical algebraic decomposition to characterize the set of parameters. It makes it possible to generate all the robot designs. A 3-RRR decoupled robot is used to validate the proposed design method.

Singular surfaces and cusps in symmetric planar 3-RPR manipulators

We study in this paper a class of 3-RPR manipulators for which the direct kinematic problem (DKP) is split into a cubic problem followed by a quadratic one. These manipulators are geometrically characterized by the fact that the moving triangle is the image of the base triangle by an indirect isometry. We introduce a specific coordinate system adapted to this geometric feature and which is also well adapted to the splitting of the DKP. This allows us to obtain easily precise descriptions of the singularities and of the cusp edges. These latter second order singularities are important for nonsingular assembly mode changing. We show how to sort assembly modes and use this sorting for motion planning in the joint space.