Hidden cusps
Paper and Code
Apr 29, 2016
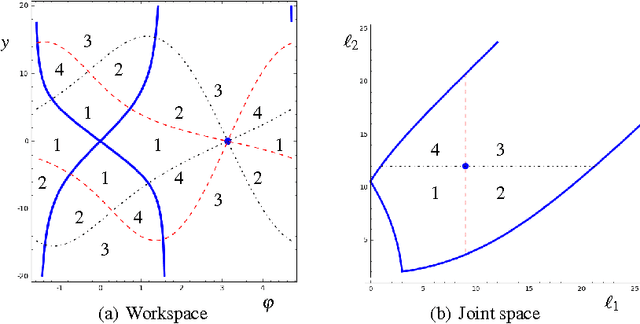


This paper investigates a situation pointed out in a recent paper, in which a non-singular change of assembly mode of a planar 2-RPR-PR parallel manipulator was realized by encircling a point of multiplicity 4. It is shown that this situation is, in fact, a non-generic one and gives rise to cusps under a small perturbation. Furthermore , we show that, for a large class of singularities of multiplicity 4, there are only two types of stable singularities occurring in a small perturbation: these two types are given by the complex square mapping and the quarto mapping. Incidentally , this paper confirms the fact that, generically, a local non-singular change of solution must be accomplished by encircling a cusp point.
* 15th International Symposium on Advances in Robot Kinematics, Jun
2016, Grasse, France. 2016
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge