Hidden cusps

This paper investigates a situation pointed out in a recent paper, in which a non-singular change of assembly mode of a planar 2-RPR-PR parallel manipulator was realized by encircling a point of multiplicity 4. It is shown that this situation is, in fact, a non-generic one and gives rise to cusps under a small perturbation. Furthermore , we show that, for a large class of singularities of multiplicity 4, there are only two types of stable singularities occurring in a small perturbation: these two types are given by the complex square mapping and the quarto mapping. Incidentally , this paper confirms the fact that, generically, a local non-singular change of solution must be accomplished by encircling a cusp point.

Singular surfaces and cusps in symmetric planar 3-RPR manipulators

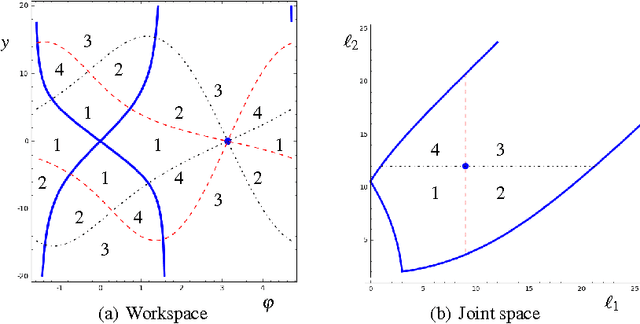
We study in this paper a class of 3-RPR manipulators for which the direct kinematic problem (DKP) is split into a cubic problem followed by a quadratic one. These manipulators are geometrically characterized by the fact that the moving triangle is the image of the base triangle by an indirect isometry. We introduce a specific coordinate system adapted to this geometric feature and which is also well adapted to the splitting of the DKP. This allows us to obtain easily precise descriptions of the singularities and of the cusp edges. These latter second order singularities are important for nonsingular assembly mode changing. We show how to sort assembly modes and use this sorting for motion planning in the joint space.