Analyse du besoin en assistance robotique dans la chirurgie de l'oreille

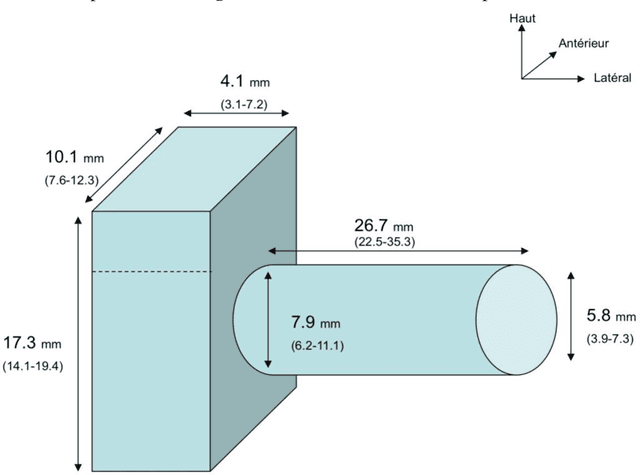
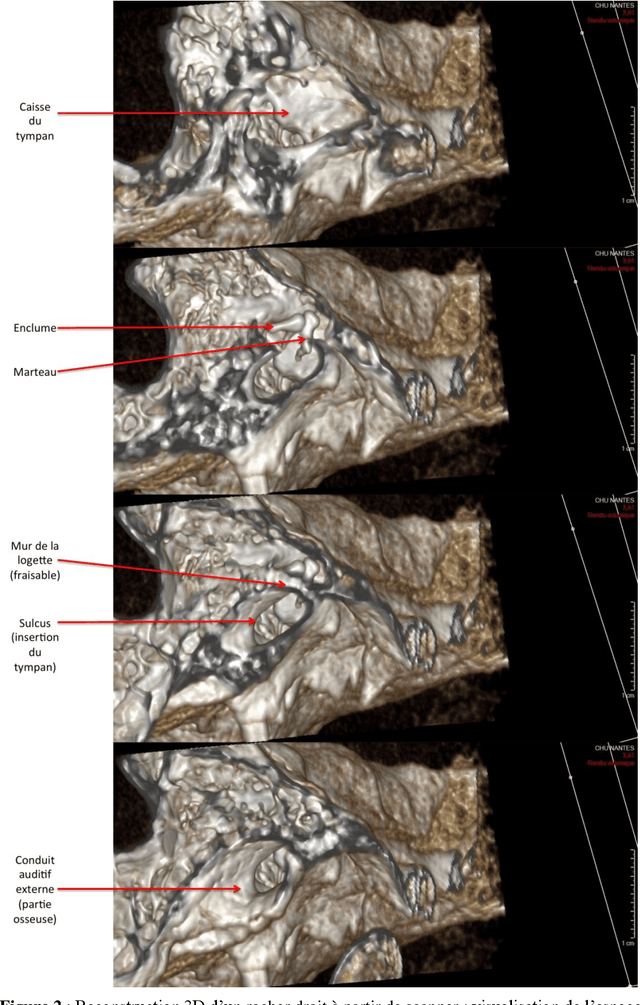
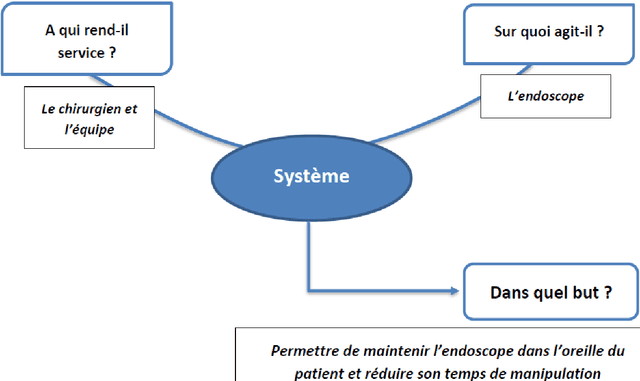
Otologic surgery has some specificities compared to others surgeries. The anatomic working space is small, with various anatomical structures to preserve, like ossicles or facial nerve. This requires the use of microscope or endoscope. The microscope let the surgeon use both hands, but allows only direct vision. The endoscope leaves only one hand to the surgeon to use his tools, but provides a "fish-eye" vision. The rise of endoscopy these past few years has led to the development of numerous devices for the surgeon: the Robotol, first otological robot designed to performed some movements and hold an endoscope, or the Endofix Exo. Both devices need the hand of the surgeon to be moved. No robotic device allows the endoscope to be directed autonomously while the surgeon keeps both hands free to work, just like when he is working with a microscope. The objective of our work is to define the specific needs of the otological assistance surgery.

Etat de l'art des systèmes robotisés en vue d'une application pour la chirurgie otologique

This article deals with a patents state-of-the-art linked to our robotic system which holds an endoscope. In a first part, we analyze how the endoscope operates as well as we discover the environment where we wish to use it: the middle ear. In a second step, we establish a state-of-the-art on patents existing in the robotic and surgical fields. The approach is based on a specific search methodology using keywords and classifications. Thanks to all the patents found, we gather them according their country and date of publication, and we are able to analyze the results. This study brings to light technical solutions invented in recent years and allows us to find an innovative research axis.

Kinetostatic analysis and solution classification of a class of planar tensegrity mechanisms

Tensegrity mechanisms are composed of rigid and tensile parts that are in equilibrium. They are interesting alternative designs for some applications, such as modelling musculo-skeleton systems. Tensegrity mechanisms are more difficult to analyze than classical mechanisms as the static equilibrium conditions that must be satisfied generally result in complex equations. A class of planar one-degree-of-freedom tensegrity mechanisms with three linear springs is analyzed in detail for the sake of systematic solution classifications. The kinetostatic equations are derived and solved under several loading and geometric conditions. It is shown that these mechanisms exhibit up to six equilibrium configurations, of which one or two are stable, depending on the geometric and loading conditions. Discriminant varieties and cylindrical algebraic decomposition combined with Groebner base elimination are used to classify solutions as a function of the geometric, loading and actuator input parameters.