Christoforos Spartalis
ReV, LS2N
Necessary and sufficient condition for a generic 3R serial manipulator to be cuspidal
Feb 17, 2022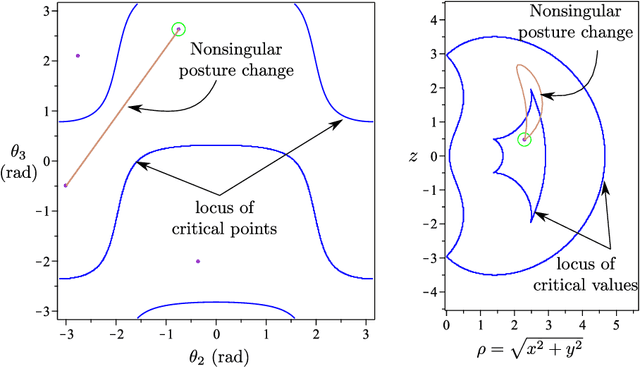
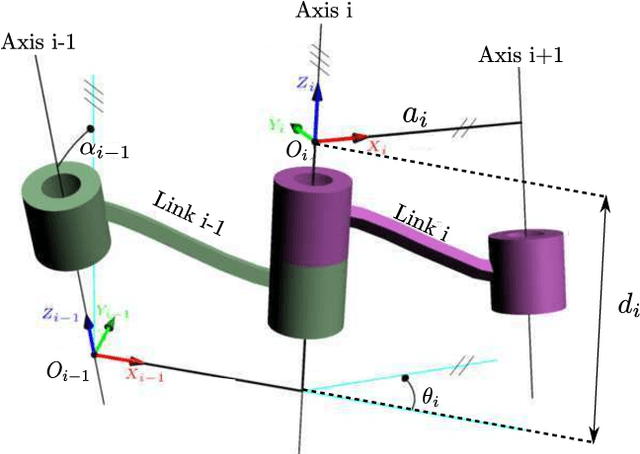
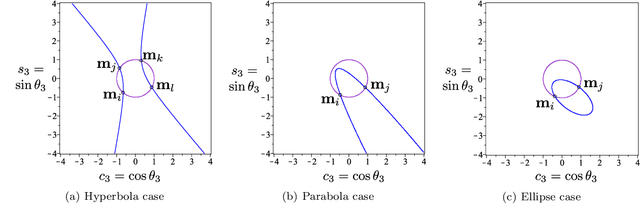

Abstract:Cuspidal robots can travel from one inverse kinematic solution to another without meeting a singularity. The name cuspidal was coined based on the existence of a cusp point in the workspace of 3R serial robots. The existence of a cusp point was proved to be a necessary and sufficient condition for orthogonal robots to be cuspidal, but it was not possible to extend this condition to non-orthogonal robots. The goal of this paper is to prove that this condition stands for any generic 3R robot. This result would give the designer more flexibility. In the presented work, the geometrical interpretation of the inverse kinematics of 3R robots is revisited and important observations on the nonsingular change of posture are noted. The paper presents a theorem regarding the existence of reduced aspects in any generic 3R serial robot. Based on these observations and on this theorem, we prove that the existence of a cusp point is a necessary and sufficient condition for any 3R generic robot to be cuspidal.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge