The assembly modes of rigid 11-bar linkages

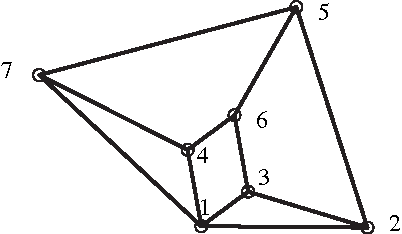
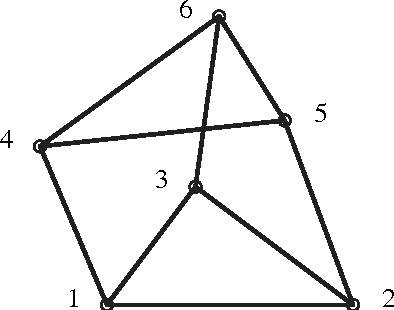
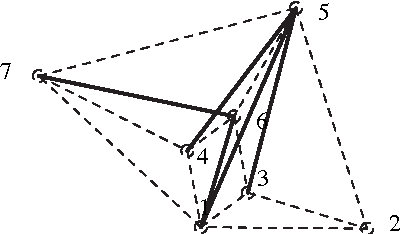
Designing an m-bar linkage with a maximal number of assembly modes is important in robot kinematics, and has further applications in structural biology and computational geometry. A related question concerns the number of assembly modes of rigid mechanisms as a function of their nodes n, which is uniquely defined given m. Rigid 11-bar linkages, where n=7, are the simplest planar linkages for which these questions were still open. It will be proven that the maximal number of assembly modes of such linkages is exactly 56. The rigidity of a linkage is captured by a polynomial system derived from distance, or Cayley-Menger, matrices. The upper bound on the number of assembly modes is obtained as the mixed volume of a 5x5 system. An 11-bar linkage admitting 56 configurations is constructed using stochastic optimisation methods. This yields a general lower bound of $\Omega(2.3^n)$ on the number of assembly modes, slightly improving the current record of $\Omega(2.289^n)$, while the best known upper bound is roughly $4^n$. Our methods are straightforward and have been implemented in Maple. They are described in general terms illustrating the fact that they can be readily extended to other planar or spatial linkages. The main results have been reported in conference publication [EM11]. This version (2017) typesets correctly the last Figure 5 so as to include all 28 configurations modulo reflection.

An algebraic method to check the singularity-free paths for parallel robots

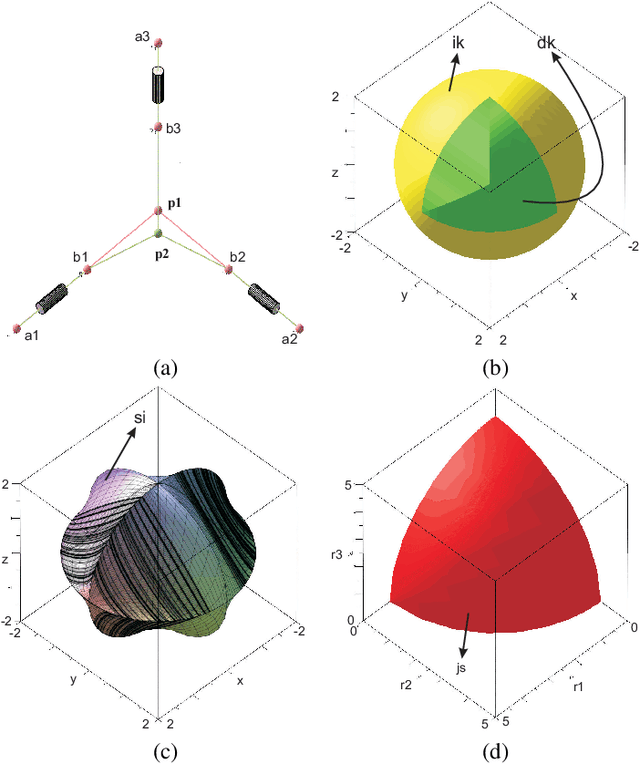
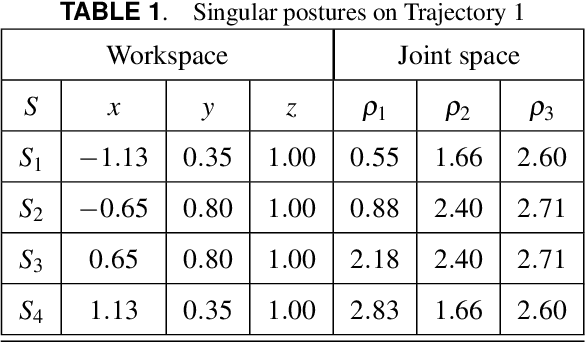
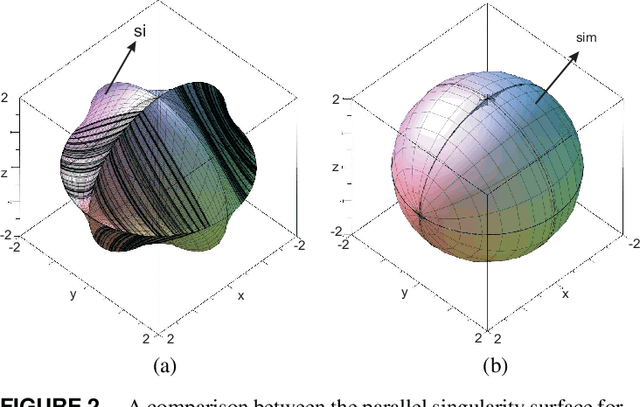
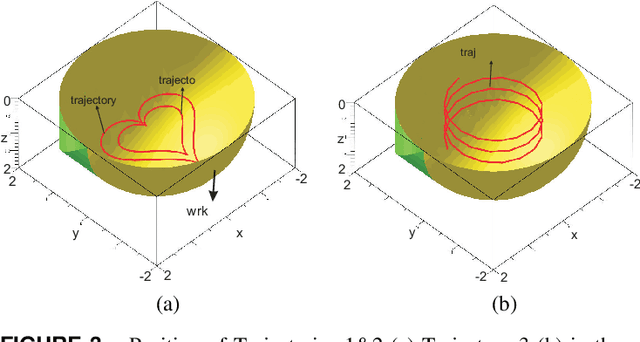
Trajectory planning is a critical step while programming the parallel manipulators in a robotic cell. The main problem arises when there exists a singular configuration between the two poses of the end-effectors while discretizing the path with a classical approach. This paper presents an algebraic method to check the feasibility of any given trajectories in the workspace. The solutions of the polynomial equations associated with the tra-jectories are projected in the joint space using Gr{\"o}bner based elimination methods and the remaining equations are expressed in a parametric form where the articular variables are functions of time t unlike any numerical or discretization method. These formal computations allow to write the Jacobian of the manip-ulator as a function of time and to check if its determinant can vanish between two poses. Another benefit of this approach is to use a largest workspace with a more complex shape than a cube, cylinder or sphere. For the Orthoglide, a three degrees of freedom parallel robot, three different trajectories are used to illustrate this method.

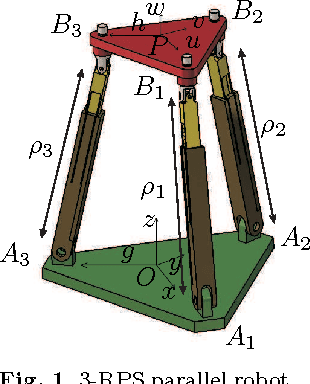
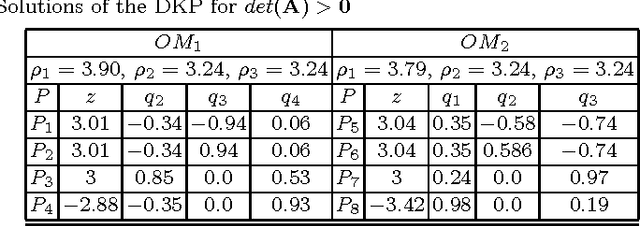
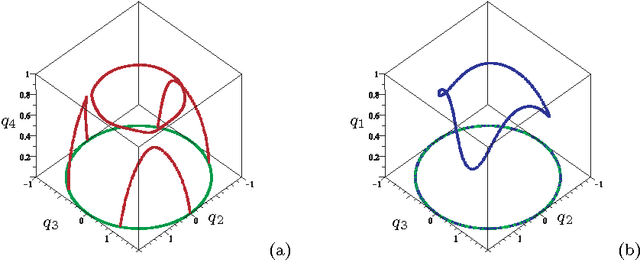
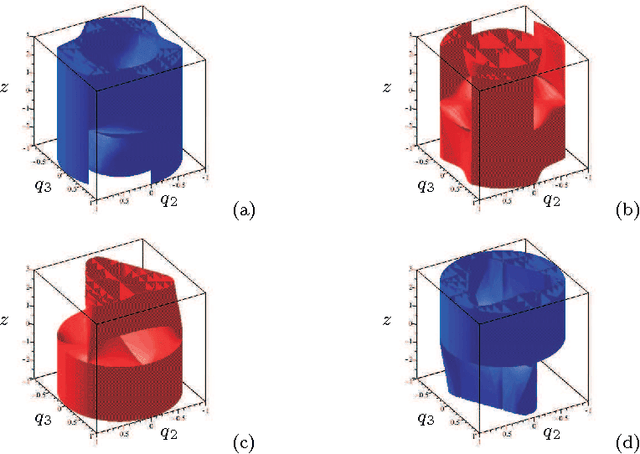
Non-singular assembly mode changing trajectories in the workspace for the 3-RPS parallel robot

Having non-singular assembly modes changing trajectories for the 3-RPS parallel robot is a well-known feature. The only known solution for defining such trajectory is to encircle a cusp point in the joint space. In this paper, the aspects and the characteristic surfaces are computed for each operation mode to define the uniqueness of the domains. Thus, we can easily see in the workspace that at least three assembly modes can be reached for each operation mode. To validate this property, the mathematical analysis of the determinant of the Jacobian is done. The image of these trajectories in the joint space is depicted with the curves associated with the cusp points.

Cusp Points in the Parameter Space of Degenerate 3-RPR Planar Parallel Manipulators

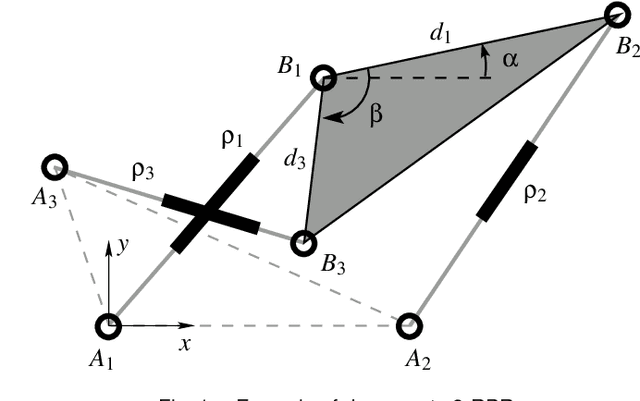
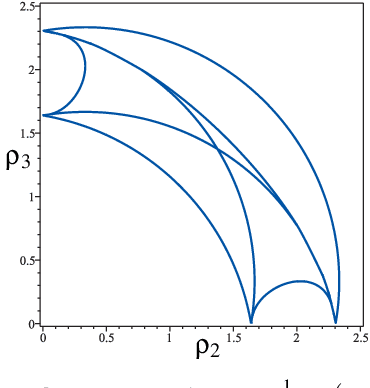
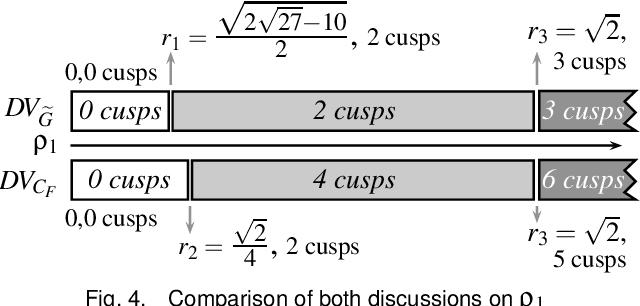
This paper investigates the conditions in the design parameter space for the existence and distribution of the cusp locus for planar parallel manipulators. Cusp points make possible non-singular assembly-mode changing motion, which increases the maximum singularity-free workspace. An accurate algorithm for the determination is proposed amending some imprecisions done by previous existing algorithms. This is combined with methods of Cylindric Algebraic Decomposition, Gr\"obner bases and Discriminant Varieties in order to partition the parameter space into cells with constant number of cusp points. These algorithms will allow us to classify a family of degenerate 3-RPR manipulators.

Solution regions in the parameter space of a 3-RRR decoupled robot for a prescribed workspace

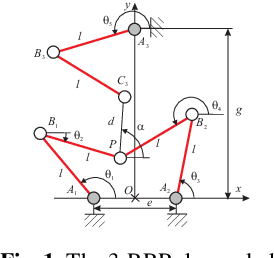
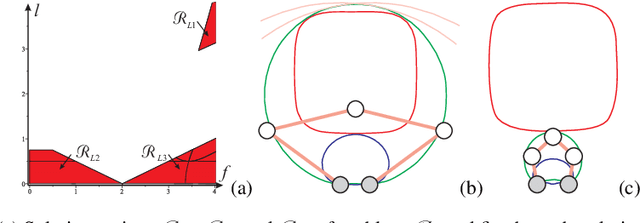
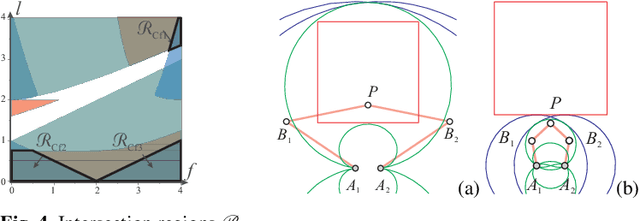
This paper proposes a new design method to determine the feasible set of parameters of translational or position/orientation decoupled parallel robots for a prescribed singularity-free workspace of regular shape. The suggested method uses Groebner bases to define the singularities and the cylindrical algebraic decomposition to characterize the set of parameters. It makes it possible to generate all the robot designs. A 3-RRR decoupled robot is used to validate the proposed design method.

Uniqueness domains and non singular assembly mode changing trajectories

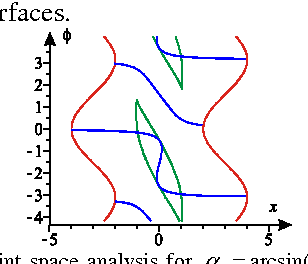
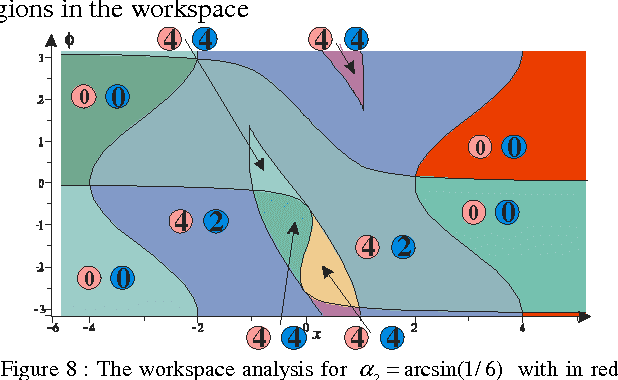
Parallel robots admit generally several solutions to the direct kinematics problem. The aspects are associated with the maximal singularity free domains without any singular configurations. Inside these regions, some trajectories are possible between two solutions of the direct kinematic problem without meeting any type of singularity: non-singular assembly mode trajectories. An established condition for such trajectories is to have cusp points inside the joint space that must be encircled. This paper presents an approach based on the notion of uniqueness domains to explain this behaviour.