On a Software Joint Velocity Limitation of a Spherical Parallel Manipulator with Coaxial Input Shafts

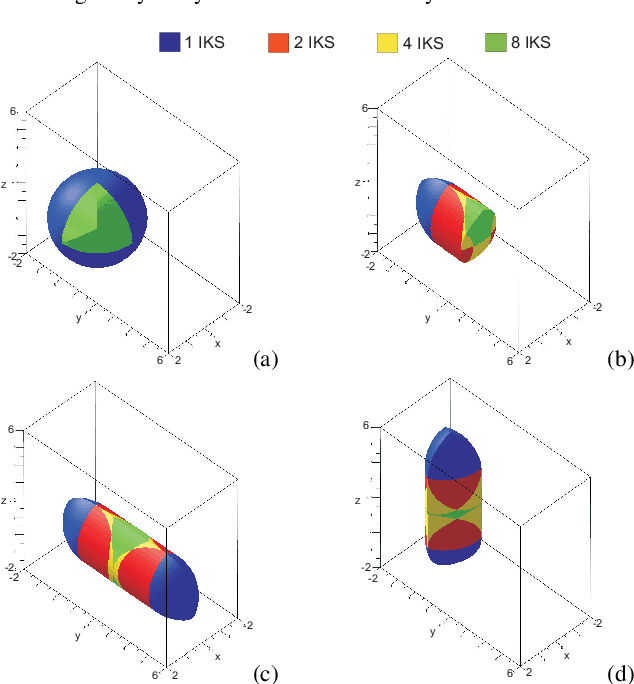
This article discusses the implementation of a software joint velocity limitation dedicated to a Spherical Parallel Manipulator (SPM) with coaxial input shafts (CoSPM) using a speed control loop. Such an algorithm takes as input the current joint positions as well as the joint reference velocities computed by the speed controller and limit the latter in order to avoid any known singular configuration. This limitation takes into account the workspace properties of the mechanism and the physical characteristics of its actuators. In particular, one takes advantage of the coaxiality of the input shafts of the CoSPM and the resulting unlimited bearing.

Inertial Line-Of-Sight Stabilization Using a 3-DOF Spherical Parallel Manipulator with Coaxial Input Shafts

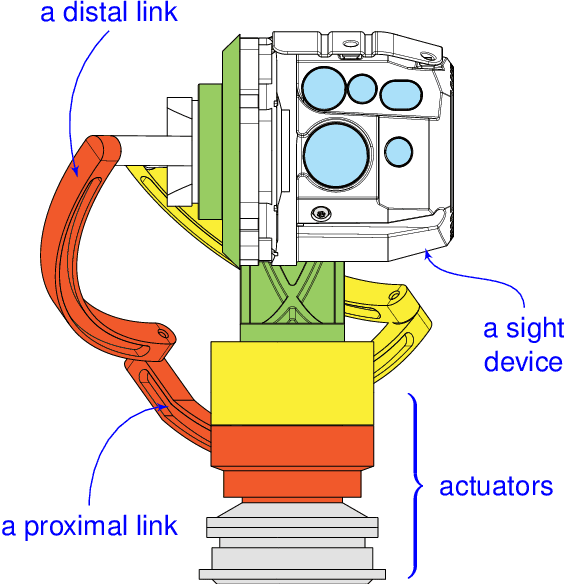
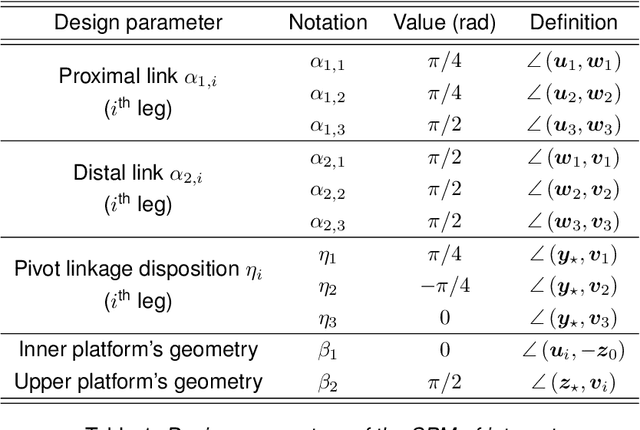
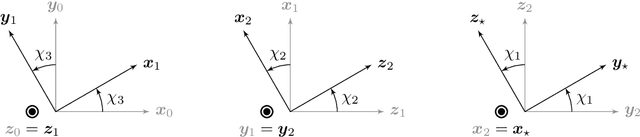
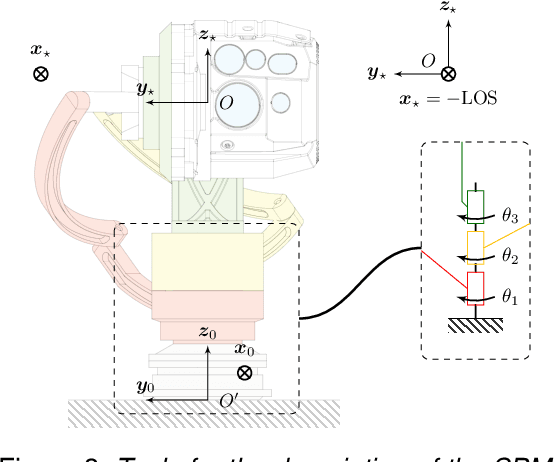
This article dives into the use of a 3-RRR Spherical Parallel Manipulator (SPM) for the purpose of inertial Line Of Sight (LOS) stabilization. Such a parallel robot provides three Degrees of Freedom (DOF) in orientation and is studied from the kinematic point of view. In particular, one guarantees that the singular loci (with the resulting numerical instabilities and inappropriate behavior of the mechanism) are far away from the prescribed workspace. Once the kinematics of the device is certified, a control strategy needs to be implemented in order to stabilize the LOS through the upper platform of the mechanism. Such a work is done with MATLAB Simulink using a SimMechanics model of our robot.

An algebraic method to check the singularity-free paths for parallel robots

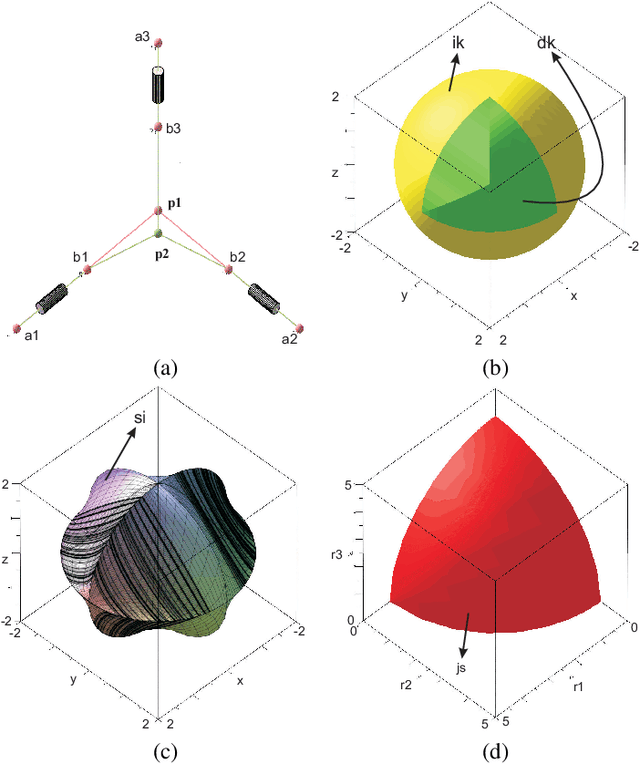
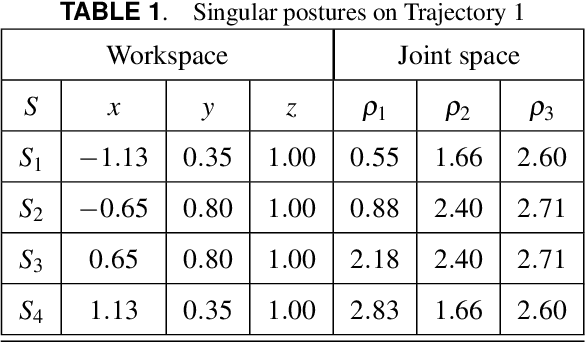
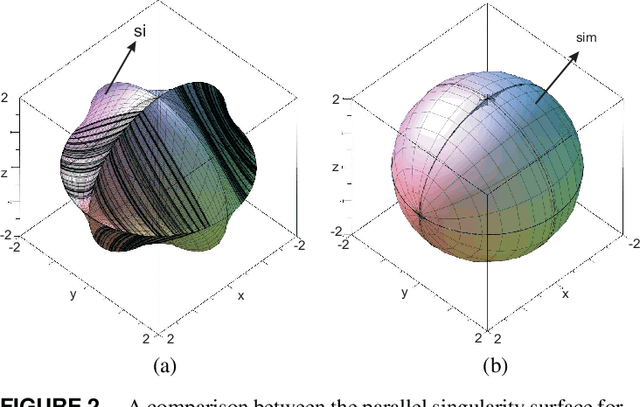
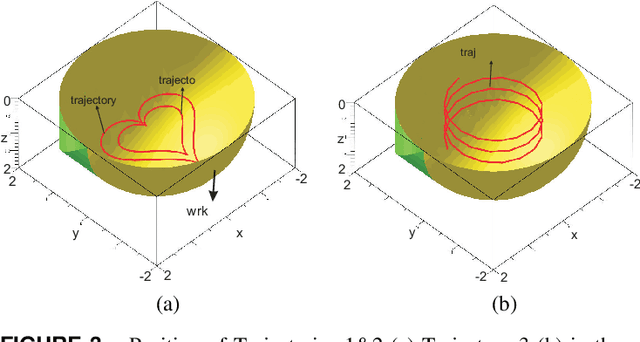
Trajectory planning is a critical step while programming the parallel manipulators in a robotic cell. The main problem arises when there exists a singular configuration between the two poses of the end-effectors while discretizing the path with a classical approach. This paper presents an algebraic method to check the feasibility of any given trajectories in the workspace. The solutions of the polynomial equations associated with the tra-jectories are projected in the joint space using Gr{\"o}bner based elimination methods and the remaining equations are expressed in a parametric form where the articular variables are functions of time t unlike any numerical or discretization method. These formal computations allow to write the Jacobian of the manip-ulator as a function of time and to check if its determinant can vanish between two poses. Another benefit of this approach is to use a largest workspace with a more complex shape than a cube, cylinder or sphere. For the Orthoglide, a three degrees of freedom parallel robot, three different trajectories are used to illustrate this method.

Workspace and Singularity analysis of a Delta like family robot

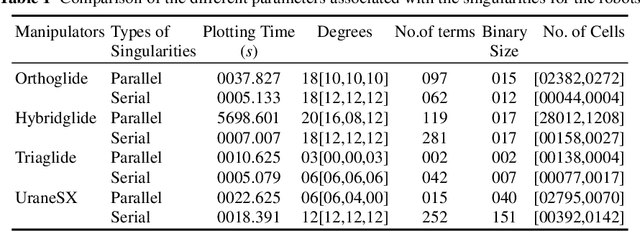
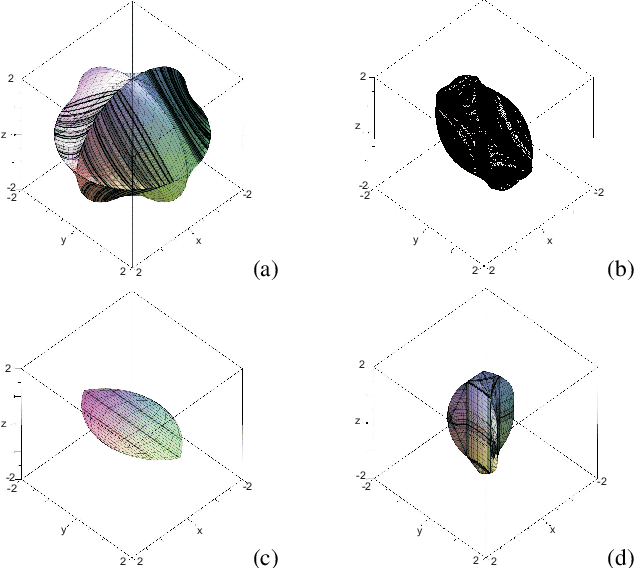
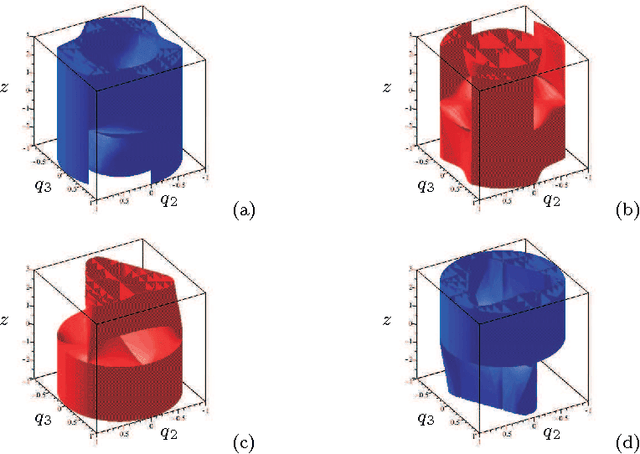
Workspace and joint space analysis are essential steps in describing the task and designing the control loop of the robot, respectively. This paper presents the descriptive analysis of a family of delta-like parallel robots by using algebraic tools to induce an estimation about the complexity in representing the singularities in the workspace and the joint space. A Gr{\"o}bner based elimination is used to compute the singularities of the manipulator and a Cylindrical Algebraic Decomposition algorithm is used to study the workspace and the joint space. From these algebraic objects, we propose some certified three dimensional plotting describing the the shape of workspace and of the joint space which will help the engineers or researchers to decide the most suited configuration of the manipulator they should use for a given task. Also, the different parameters associated with the complexity of the serial and parallel singularities are tabulated, which further enhance the selection of the different configuration of the manipulator by comparing the complexity of the singularity equations.

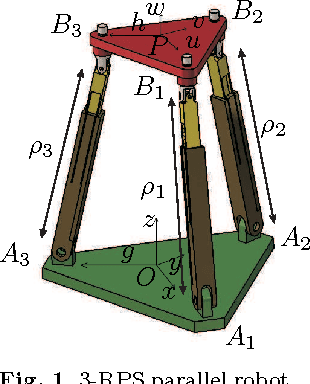
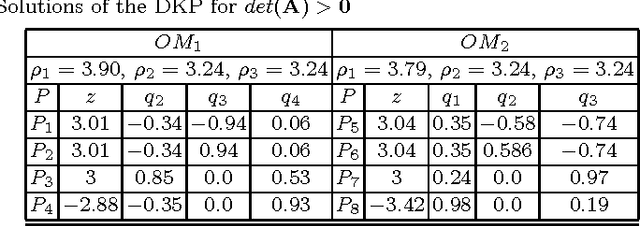
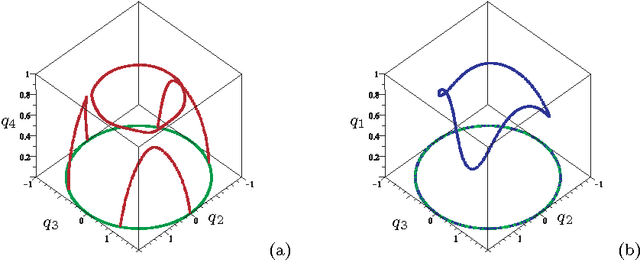
Non-singular assembly mode changing trajectories in the workspace for the 3-RPS parallel robot

Having non-singular assembly modes changing trajectories for the 3-RPS parallel robot is a well-known feature. The only known solution for defining such trajectory is to encircle a cusp point in the joint space. In this paper, the aspects and the characteristic surfaces are computed for each operation mode to define the uniqueness of the domains. Thus, we can easily see in the workspace that at least three assembly modes can be reached for each operation mode. To validate this property, the mathematical analysis of the determinant of the Jacobian is done. The image of these trajectories in the joint space is depicted with the curves associated with the cusp points.

Cusp Points in the Parameter Space of Degenerate 3-RPR Planar Parallel Manipulators

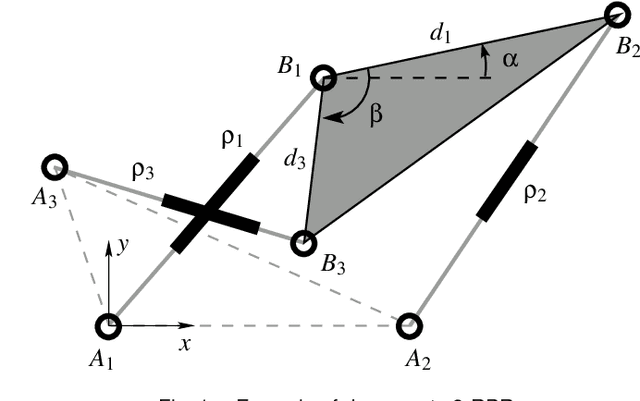
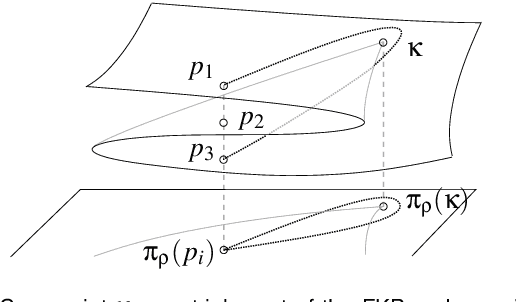
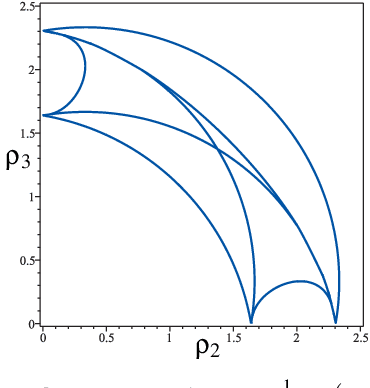
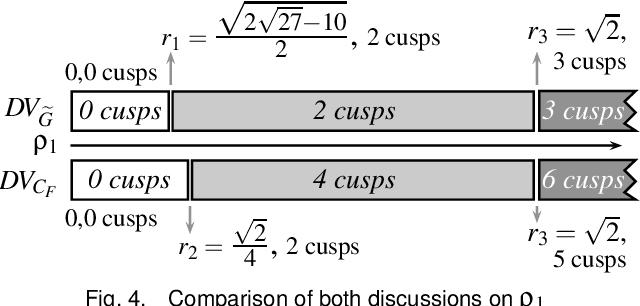
This paper investigates the conditions in the design parameter space for the existence and distribution of the cusp locus for planar parallel manipulators. Cusp points make possible non-singular assembly-mode changing motion, which increases the maximum singularity-free workspace. An accurate algorithm for the determination is proposed amending some imprecisions done by previous existing algorithms. This is combined with methods of Cylindric Algebraic Decomposition, Gr\"obner bases and Discriminant Varieties in order to partition the parameter space into cells with constant number of cusp points. These algorithms will allow us to classify a family of degenerate 3-RPR manipulators.