An algebraic method to check the singularity-free paths for parallel robots
Paper and Code
May 26, 2015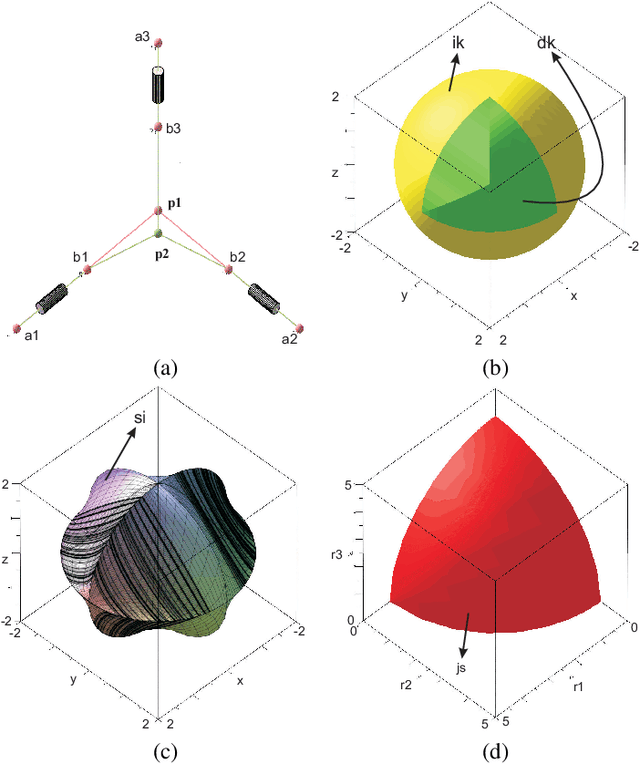
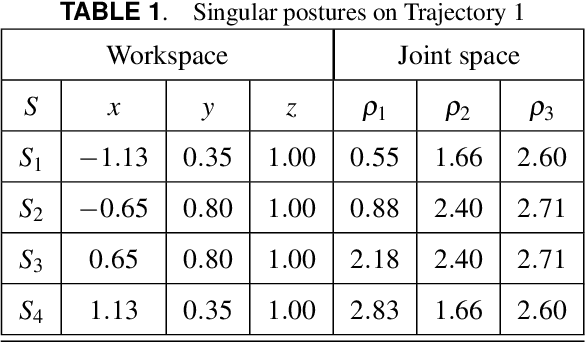
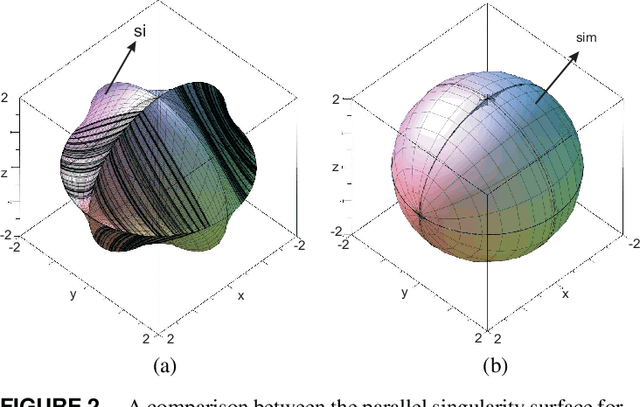
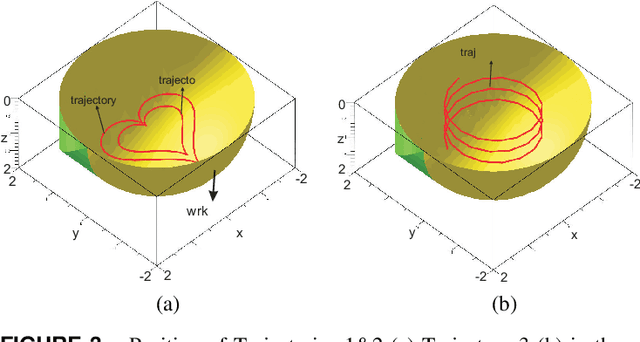
Trajectory planning is a critical step while programming the parallel manipulators in a robotic cell. The main problem arises when there exists a singular configuration between the two poses of the end-effectors while discretizing the path with a classical approach. This paper presents an algebraic method to check the feasibility of any given trajectories in the workspace. The solutions of the polynomial equations associated with the tra-jectories are projected in the joint space using Gr{\"o}bner based elimination methods and the remaining equations are expressed in a parametric form where the articular variables are functions of time t unlike any numerical or discretization method. These formal computations allow to write the Jacobian of the manip-ulator as a function of time and to check if its determinant can vanish between two poses. Another benefit of this approach is to use a largest workspace with a more complex shape than a cube, cylinder or sphere. For the Orthoglide, a three degrees of freedom parallel robot, three different trajectories are used to illustrate this method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge