The assembly modes of rigid 11-bar linkages
Paper and Code
Oct 17, 2017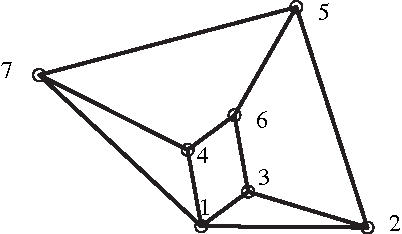
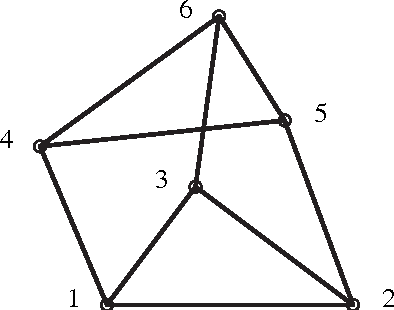
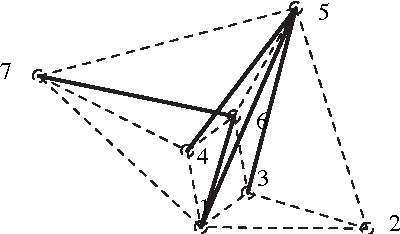
Designing an m-bar linkage with a maximal number of assembly modes is important in robot kinematics, and has further applications in structural biology and computational geometry. A related question concerns the number of assembly modes of rigid mechanisms as a function of their nodes n, which is uniquely defined given m. Rigid 11-bar linkages, where n=7, are the simplest planar linkages for which these questions were still open. It will be proven that the maximal number of assembly modes of such linkages is exactly 56. The rigidity of a linkage is captured by a polynomial system derived from distance, or Cayley-Menger, matrices. The upper bound on the number of assembly modes is obtained as the mixed volume of a 5x5 system. An 11-bar linkage admitting 56 configurations is constructed using stochastic optimisation methods. This yields a general lower bound of $\Omega(2.3^n)$ on the number of assembly modes, slightly improving the current record of $\Omega(2.289^n)$, while the best known upper bound is roughly $4^n$. Our methods are straightforward and have been implemented in Maple. They are described in general terms illustrating the fact that they can be readily extended to other planar or spatial linkages. The main results have been reported in conference publication [EM11]. This version (2017) typesets correctly the last Figure 5 so as to include all 28 configurations modulo reflection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge