Identifiability and generalizability from multiple experts in Inverse Reinforcement Learning

While Reinforcement Learning (RL) aims to train an agent from a reward function in a given environment, Inverse Reinforcement Learning (IRL) seeks to recover the reward function from observing an expert's behavior. It is well known that, in general, various reward functions can lead to the same optimal policy, and hence, IRL is ill-defined. However, (Cao et al., 2021) showed that, if we observe two or more experts with different discount factors or acting in different environments, the reward function can under certain conditions be identified up to a constant. This work starts by showing an equivalent identifiability statement from multiple experts in tabular MDPs based on a rank condition, which is easily verifiable and is shown to be also necessary. We then extend our result to various different scenarios, i.e., we characterize reward identifiability in the case where the reward function can be represented as a linear combination of given features, making it more interpretable, or when we have access to approximate transition matrices. Even when the reward is not identifiable, we provide conditions characterizing when data on multiple experts in a given environment allows to generalize and train an optimal agent in a new environment. Our theoretical results on reward identifiability and generalizability are validated in various numerical experiments.

Score matching enables causal discovery of nonlinear additive noise models

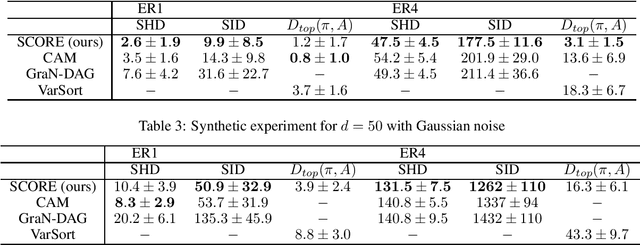
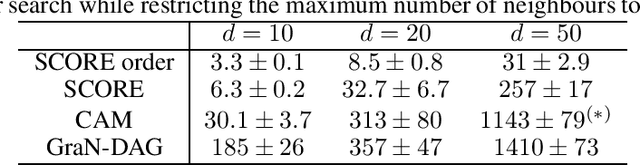
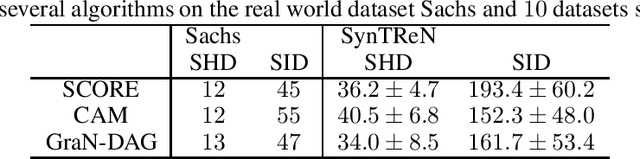
This paper demonstrates how to recover causal graphs from the score of the data distribution in non-linear additive (Gaussian) noise models. Using score matching algorithms as a building block, we show how to design a new generation of scalable causal discovery methods. To showcase our approach, we also propose a new efficient method for approximating the score's Jacobian, enabling to recover the causal graph. Empirically, we find that the new algorithm, called SCORE, is competitive with state-of-the-art causal discovery methods while being significantly faster.

Efficient Proximal Mapping of the 1-path-norm of Shallow Networks

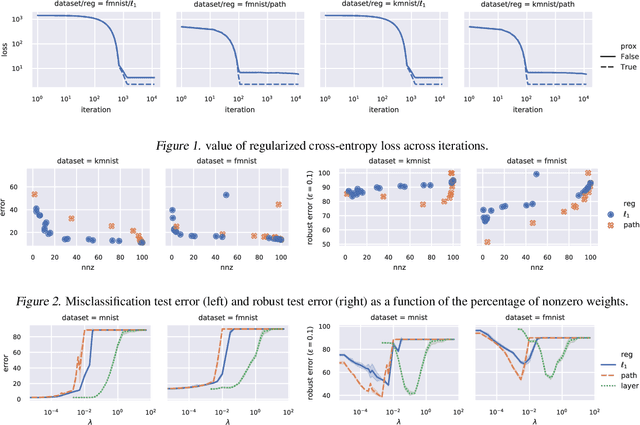
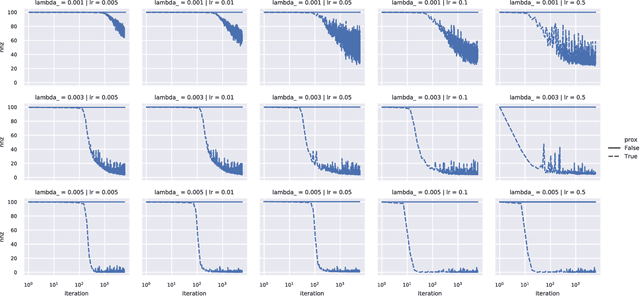
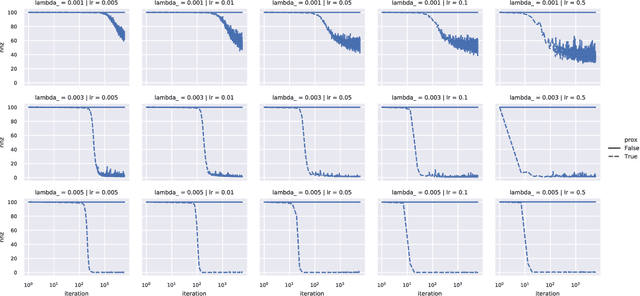
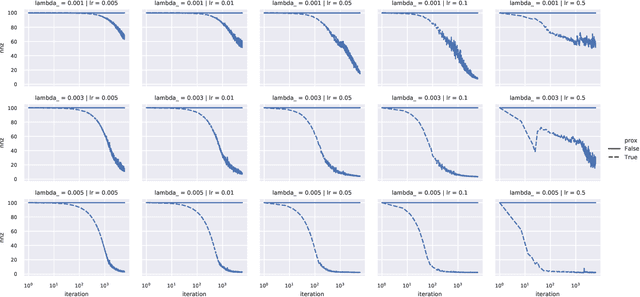
We demonstrate two new important properties of the 1-path-norm of shallow neural networks. First, despite its non-smoothness and non-convexity it allows a closed form proximal operator which can be efficiently computed, allowing the use of stochastic proximal-gradient-type methods for regularized empirical risk minimization. Second, when the activation functions is differentiable, it provides an upper bound on the Lipschitz constant of the network. Such bound is tighter than the trivial layer-wise product of Lipschitz constants, motivating its use for training networks robust to adversarial perturbations. In practical experiments we illustrate the advantages of using the proximal mapping and we compare the robustness-accuracy trade-off induced by the 1-path-norm, L1-norm and layer-wise constraints on the Lipschitz constant (Parseval networks).

Lipschitz constant estimation of Neural Networks via sparse polynomial optimization

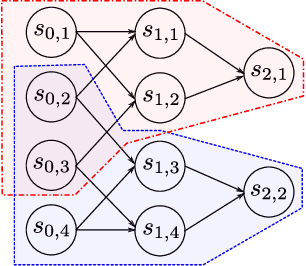
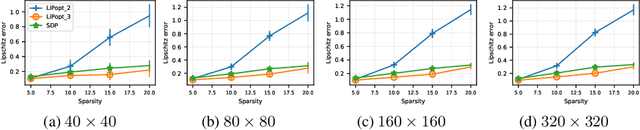
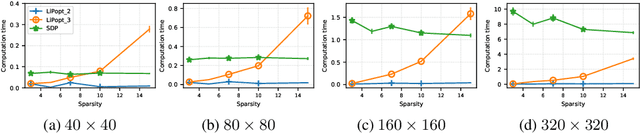
We introduce LiPopt, a polynomial optimization framework for computing increasingly tighter upper bounds on the Lipschitz constant of neural networks. The underlying optimization problems boil down to either linear (LP) or semidefinite (SDP) programming. We show how to use the sparse connectivity of a network, to significantly reduce the complexity of computation. This is specially useful for convolutional as well as pruned neural networks. We conduct experiments on networks with random weights as well as networks trained on MNIST, showing that in the particular case of the $\ell_\infty$-Lipschitz constant, our approach yields superior estimates, compared to baselines available in the literature.

Robust Reinforcement Learning via Adversarial training with Langevin Dynamics

We introduce a sampling perspective to tackle the challenging task of training robust Reinforcement Learning (RL) agents. Leveraging the powerful Stochastic Gradient Langevin Dynamics, we present a novel, scalable two-player RL algorithm, which is a sampling variant of the two-player policy gradient method. Our algorithm consistently outperforms existing baselines, in terms of generalization across different training and testing conditions, on several MuJoCo environments. Our experiments also show that, even for objective functions that entirely ignore potential environmental shifts, our sampling approach remains highly robust in comparison to standard RL algorithms.

Efficient learning of smooth probability functions from Bernoulli tests with guarantees

We study the fundamental problem of learning an unknown, smooth probability function via point-wise Bernoulli tests. We provide the first scalable algorithm for efficiently solving this problem with rigorous guarantees. In particular, we prove the convergence rate of our posterior update rule to the true probability function in L2-norm. Moreover, we allow the Bernoulli tests to depend on contextual features, and provide a modified inference engine with provable guarantees for this novel setting. Numerical results show that the empirical convergence rates match the theory, and illustrate the superiority of our approach in handling contextual features over the state-of-the-art.

Mirrored Langevin Dynamics

We consider the problem of sampling from constrained distributions, which has posed significant challenges to both non-asymptotic analysis and algorithmic design. We propose a unified framework, which is inspired by the classical mirror descent, to derive novel first-order sampling schemes. We prove that, for a general target distribution with strongly convex potential, our framework implies the existence of a first-order algorithm achieving $\tilde{O}(\epsilon^{-2}d)$ convergence, suggesting that the state-of-the-art $\tilde{O}(\epsilon^{-6}d^5)$ can be vastly improved. With the important Latent Dirichlet Allocation (LDA) application in mind, we specialize our algorithm to sample from Dirichlet posteriors, and derive the first non-asymptotic $\tilde{O}(\epsilon^{-2}d^2)$ rate for first-order sampling. We further extend our framework to the mini-batch setting and prove convergence rates when only stochastic gradients are available. Finally, we report promising experimental results for LDA on real datasets.

High-Dimensional Bayesian Optimization via Additive Models with Overlapping Groups

Bayesian optimization (BO) is a popular technique for sequential black-box function optimization, with applications including parameter tuning, robotics, environmental monitoring, and more. One of the most important challenges in BO is the development of algorithms that scale to high dimensions, which remains a key open problem despite recent progress. In this paper, we consider the approach of Kandasamy et al. (2015), in which the high-dimensional function decomposes as a sum of lower-dimensional functions on subsets of the underlying variables. In particular, we significantly generalize this approach by lifting the assumption that the subsets are disjoint, and consider additive models with arbitrary overlap among the subsets. By representing the dependencies via a graph, we deduce an efficient message passing algorithm for optimizing the acquisition function. In addition, we provide an algorithm for learning the graph from samples based on Gibbs sampling. We empirically demonstrate the effectiveness of our methods on both synthetic and real-world data.