Regret minimization in stochastic non-convex learning via a proximal-gradient approach

Motivated by applications in machine learning and operations research, we study regret minimization with stochastic first-order oracle feedback in online constrained, and possibly non-smooth, non-convex problems. In this setting, the minimization of external regret is beyond reach for first-order methods, so we focus on a local regret measure defined via a proximal-gradient mapping. To achieve no (local) regret in this setting, we develop a prox-grad method based on stochastic first-order feedback, and a simpler method for when access to a perfect first-order oracle is possible. Both methods are min-max order-optimal, and we also establish a bound on the number of prox-grad queries these methods require. As an important application of our results, we also obtain a link between online and offline non-convex stochastic optimization manifested as a new prox-grad scheme with complexity guarantees matching those obtained via variance reduction techniques.

Efficient Proximal Mapping of the 1-path-norm of Shallow Networks

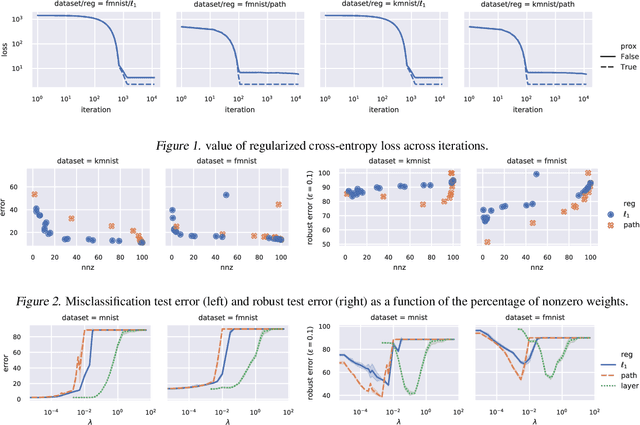
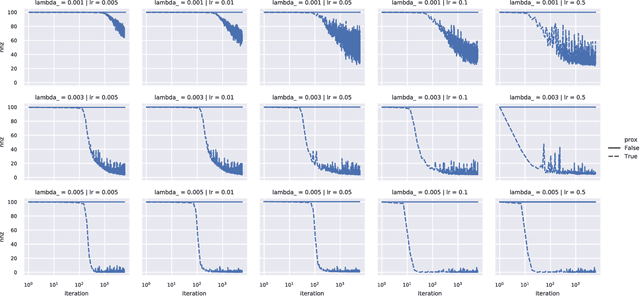
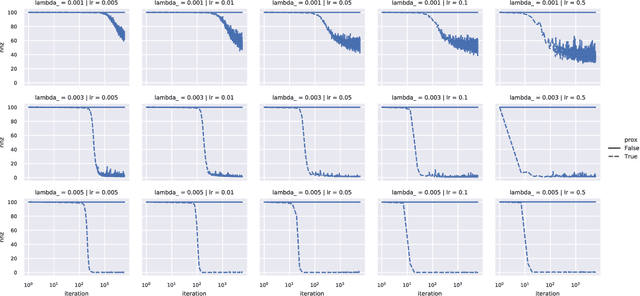
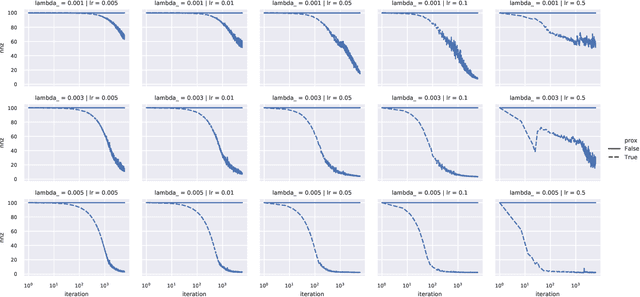
We demonstrate two new important properties of the 1-path-norm of shallow neural networks. First, despite its non-smoothness and non-convexity it allows a closed form proximal operator which can be efficiently computed, allowing the use of stochastic proximal-gradient-type methods for regularized empirical risk minimization. Second, when the activation functions is differentiable, it provides an upper bound on the Lipschitz constant of the network. Such bound is tighter than the trivial layer-wise product of Lipschitz constants, motivating its use for training networks robust to adversarial perturbations. In practical experiments we illustrate the advantages of using the proximal mapping and we compare the robustness-accuracy trade-off induced by the 1-path-norm, L1-norm and layer-wise constraints on the Lipschitz constant (Parseval networks).

On the Almost Sure Convergence of Stochastic Gradient Descent in Non-Convex Problems

This paper analyzes the trajectories of stochastic gradient descent (SGD) to help understand the algorithm's convergence properties in non-convex problems. We first show that the sequence of iterates generated by SGD remains bounded and converges with probability $1$ under a very broad range of step-size schedules. Subsequently, going beyond existing positive probability guarantees, we show that SGD avoids strict saddle points/manifolds with probability $1$ for the entire spectrum of step-size policies considered. Finally, we prove that the algorithm's rate of convergence to Hurwicz minimizers is $\mathcal{O}(1/n^{p})$ if the method is employed with a $\Theta(1/n^p)$ step-size schedule. This provides an important guideline for tuning the algorithm's step-size as it suggests that a cool-down phase with a vanishing step-size could lead to faster convergence; we demonstrate this heuristic using ResNet architectures on CIFAR.