t-SNE Exaggerates Clusters, Provably

Central to the widespread use of t-distributed stochastic neighbor embedding (t-SNE) is the conviction that it produces visualizations whose structure roughly matches that of the input. To the contrary, we prove that (1) the strength of the input clustering, and (2) the extremity of outlier points, cannot be reliably inferred from the t-SNE output. We demonstrate the prevalence of these failure modes in practice as well.

LogicLearner: A Tool for the Guided Practice of Propositional Logic Proofs

The study of propositional logic -- fundamental to the theory of computing -- is a cornerstone of the undergraduate computer science curriculum. Learning to solve logical proofs requires repeated guided practice, but undergraduate students often lack access to on-demand tutoring in a judgment-free environment. In this work, we highlight the need for guided practice tools in undergraduate mathematics education and outline the desiderata of an effective practice tool. We accordingly develop LogicLearner, a web application for guided logic proof practice. LogicLearner consists of an interface to attempt logic proofs step-by-step and an automated proof solver to generate solutions on the fly, allowing users to request guidance as needed. We pilot LogicLearner as a practice tool in two semesters of an undergraduate discrete mathematics course and receive strongly positive feedback for usability and pedagogical value in student surveys. To the best of our knowledge, LogicLearner is the only learning tool that provides an end-to-end practice environment for logic proofs with immediate, judgment-free feedback.

Using Deep Autoregressive Models as Causal Inference Engines

Existing causal inference (CI) models are limited to primarily handling low-dimensional confounders and singleton actions. We propose an autoregressive (AR) CI framework capable of handling complex confounders and sequential actions common in modern applications. We accomplish this by {\em sequencification}, transforming data from an underlying causal diagram into a sequence of tokens. This approach not only enables training with data generated from any DAG but also extends existing CI capabilities to accommodate estimating several statistical quantities using a {\em single} model. We can directly predict interventional probabilities, simplifying inference and enhancing outcome prediction accuracy. We demonstrate that an AR model adapted for CI is efficient and effective in various complex applications such as navigating mazes, playing chess endgames, and evaluating the impact of certain keywords on paper acceptance rates.

Contrastive Loss is All You Need to Recover Analogies as Parallel Lines

While static word embedding models are known to represent linguistic analogies as parallel lines in high-dimensional space, the underlying mechanism as to why they result in such geometric structures remains obscure. We find that an elementary contrastive-style method employed over distributional information performs competitively with popular word embedding models on analogy recovery tasks, while achieving dramatic speedups in training time. Further, we demonstrate that a contrastive loss is sufficient to create these parallel structures in word embeddings, and establish a precise relationship between the co-occurrence statistics and the geometric structure of the resulting word embeddings.

Improving Model Training via Self-learned Label Representations

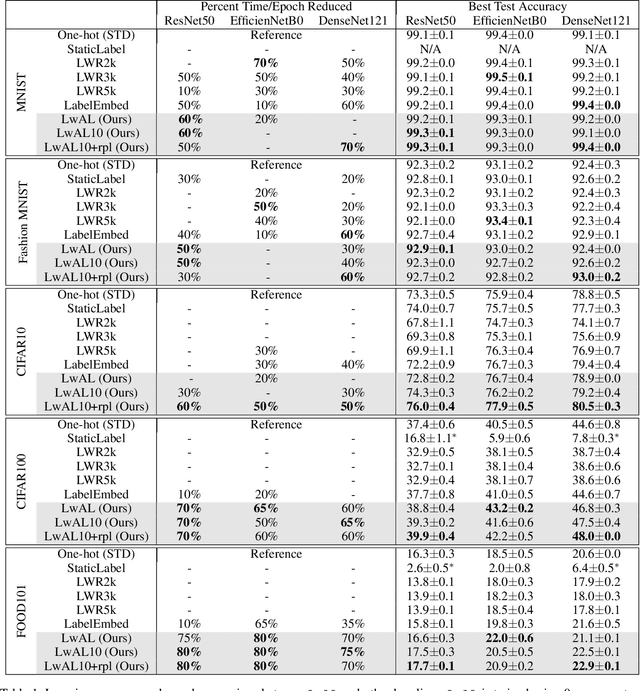
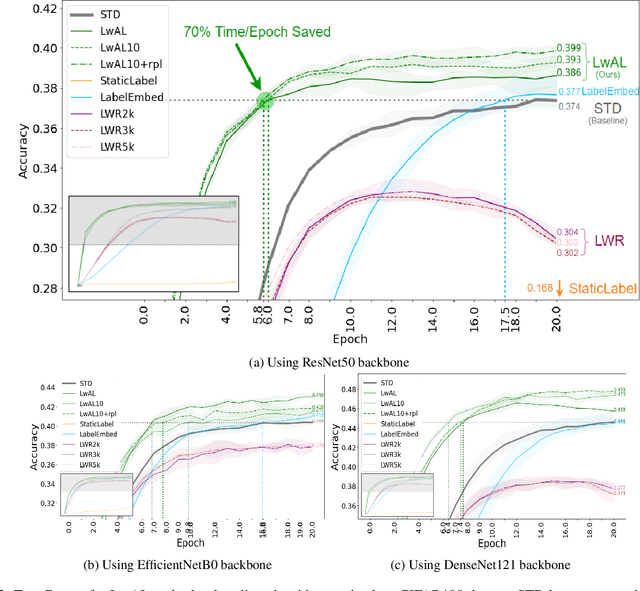
Modern neural network architectures have shown remarkable success in several large-scale classification and prediction tasks. Part of the success of these architectures is their flexibility to transform the data from the raw input representations (e.g. pixels for vision tasks, or text for natural language processing tasks) to one-hot output encoding. While much of the work has focused on studying how the input gets transformed to the one-hot encoding, very little work has examined the effectiveness of these one-hot labels. In this work, we demonstrate that more sophisticated label representations are better for classification than the usual one-hot encoding. We propose Learning with Adaptive Labels (LwAL) algorithm, which simultaneously learns the label representation while training for the classification task. These learned labels can significantly cut down on the training time (usually by more than 50%) while often achieving better test accuracies. Our algorithm introduces negligible additional parameters and has a minimal computational overhead. Along with improved training times, our learned labels are semantically meaningful and can reveal hierarchical relationships that may be present in the data.

A Neural Network Solves and Generates Mathematics Problems by Program Synthesis: Calculus, Differential Equations, Linear Algebra, and More

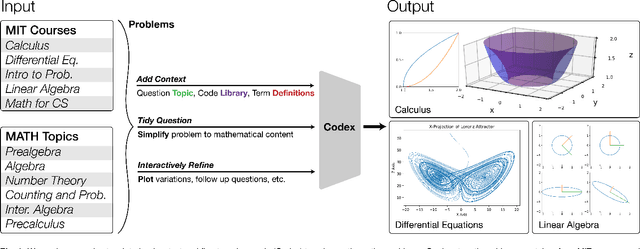
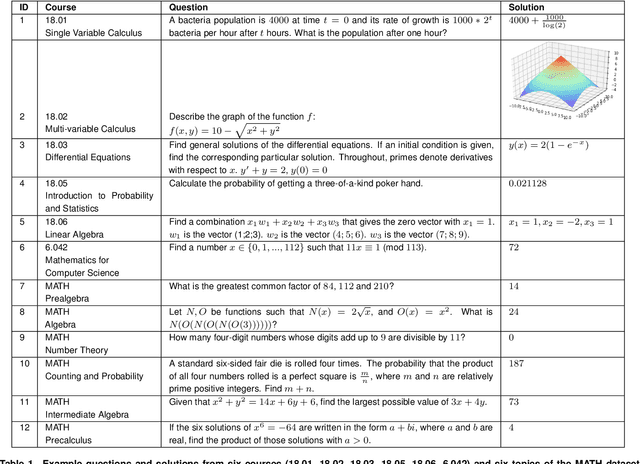
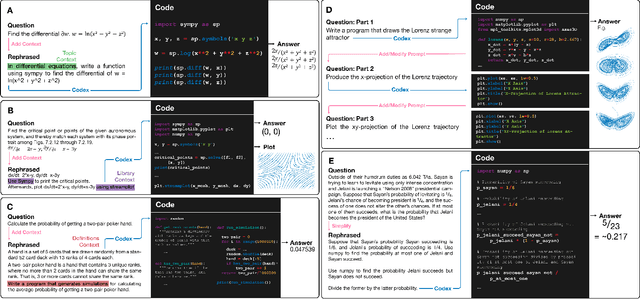
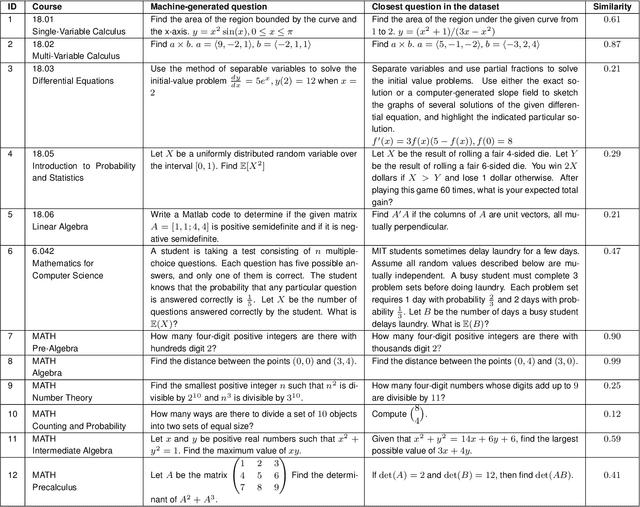
We demonstrate that a neural network pre-trained on text and fine-tuned on code solves Mathematics problems by program synthesis. We turn questions into programming tasks, automatically generate programs, and then execute them, perfectly solving university-level problems from MIT's large Mathematics courses (Single Variable Calculus 18.01, Multivariable Calculus 18.02, Differential Equations 18.03, Introduction to Probability and Statistics 18.05, Linear Algebra 18.06, and Mathematics for Computer Science 6.042), Columbia University's COMS3251 Computational Linear Algebra course, as well as questions from a MATH dataset (on Prealgebra, Algebra, Counting and Probability, Number Theory, and Precalculus), the latest benchmark of advanced mathematics problems specifically designed to assess mathematical reasoning. We explore prompt generation methods that enable Transformers to generate question solving programs for these subjects, including solutions with plots. We generate correct answers for a random sample of questions in each topic. We quantify the gap between the original and transformed questions and perform a survey to evaluate the quality and difficulty of generated questions. This is the first work to automatically solve, grade, and generate university-level Mathematics course questions at scale. This represents a milestone for higher education.

An analysis of document graph construction methods for AMR summarization

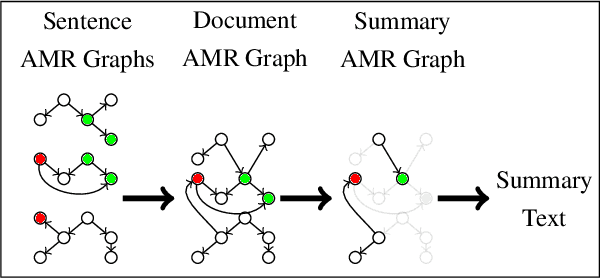
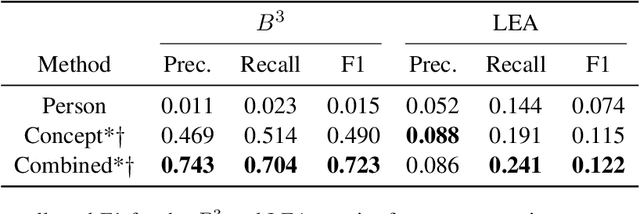
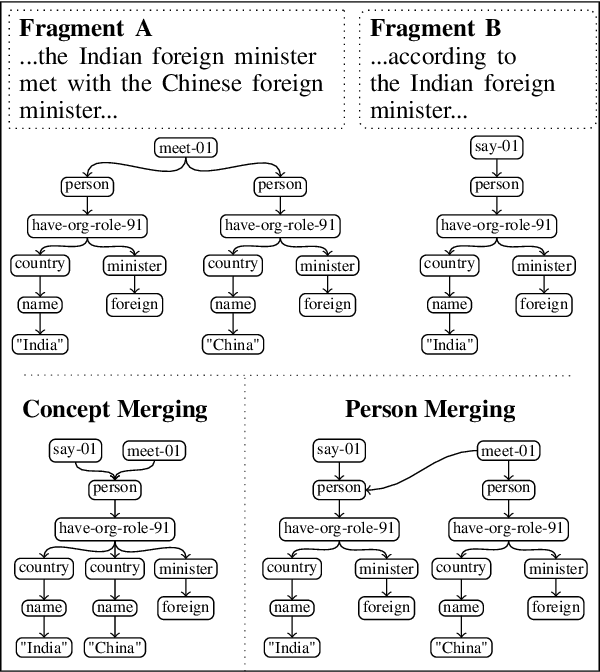
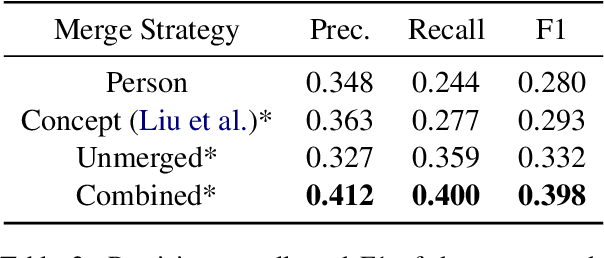
Meaning Representation (AMR) is a graph-based semantic representation for sentences, composed of collections of concepts linked by semantic relations. AMR-based approaches have found success in a variety of applications, but a challenge to using it in tasks that require document-level context is that it only represents individual sentences. Prior work in AMR-based summarization has automatically merged the individual sentence graphs into a document graph, but the method of merging and its effects on summary content selection have not been independently evaluated. In this paper, we present a novel dataset consisting of human-annotated alignments between the nodes of paired documents and summaries which may be used to evaluate (1) merge strategies; and (2) the performance of content selection methods over nodes of a merged or unmerged AMR graph. We apply these two forms of evaluation to prior work as well as a new method for node merging and show that our new method has significantly better performance than prior work.

Solving Probability and Statistics Problems by Program Synthesis

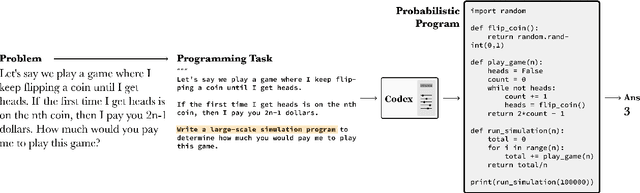
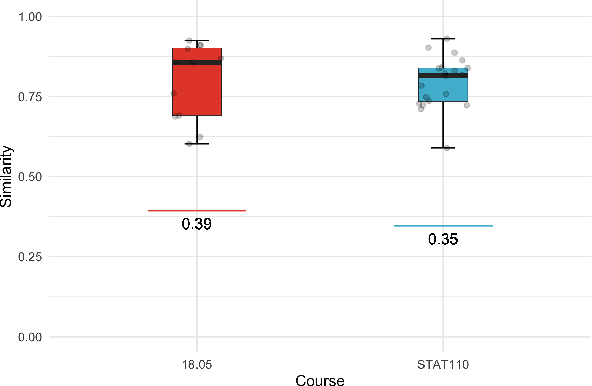
We solve university level probability and statistics questions by program synthesis using OpenAI's Codex, a Transformer trained on text and fine-tuned on code. We transform course problems from MIT's 18.05 Introduction to Probability and Statistics and Harvard's STAT110 Probability into programming tasks. We then execute the generated code to get a solution. Since these course questions are grounded in probability, we often aim to have Codex generate probabilistic programs that simulate a large number of probabilistic dependencies to compute its solution. Our approach requires prompt engineering to transform the question from its original form to an explicit, tractable form that results in a correct program and solution. To estimate the amount of work needed to translate an original question into its tractable form, we measure the similarity between original and transformed questions. Our work is the first to introduce a new dataset of university-level probability and statistics problems and solve these problems in a scalable fashion using the program synthesis capabilities of large language models.

Solving Linear Algebra by Program Synthesis

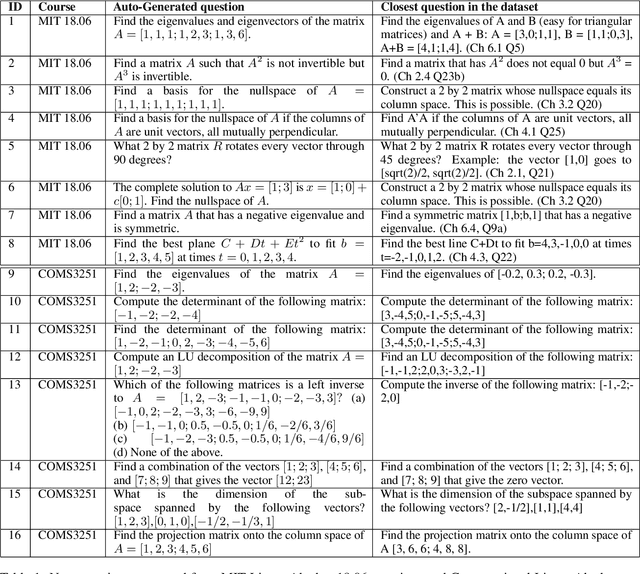
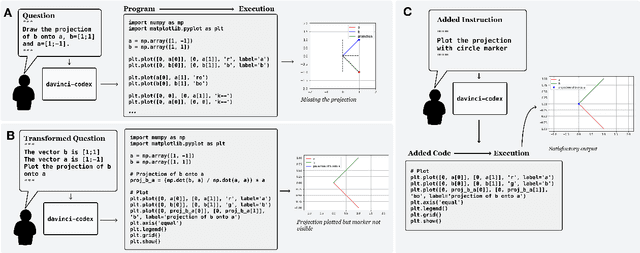
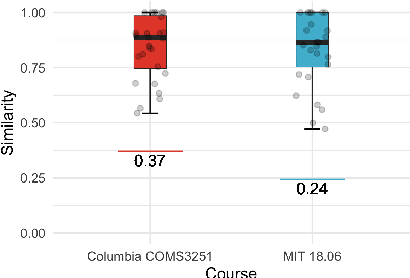
We solve MIT's Linear Algebra 18.06 course and Columbia University's Computational Linear Algebra COMS3251 courses with perfect accuracy by interactive program synthesis. This surprisingly strong result is achieved by turning the course questions into programming tasks and then running the programs to produce the correct answers. We use OpenAI Codex with zero-shot learning, without providing any examples in the prompts, to synthesize code from questions. We quantify the difference between the original question text and the transformed question text that yields a correct answer. Since all COMS3251 questions are not available online the model is not overfitting. We go beyond just generating code for questions with numerical answers by interactively generating code that also results visually pleasing plots as output. Finally, we automatically generate new questions given a few sample questions which may be used as new course content. This work is a significant step forward in solving quantitative math problems and opens the door for solving many university level STEM courses by machine.

Meta-Learning to Cluster

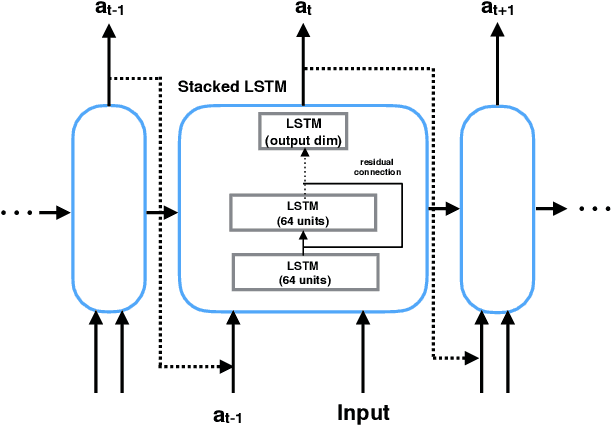
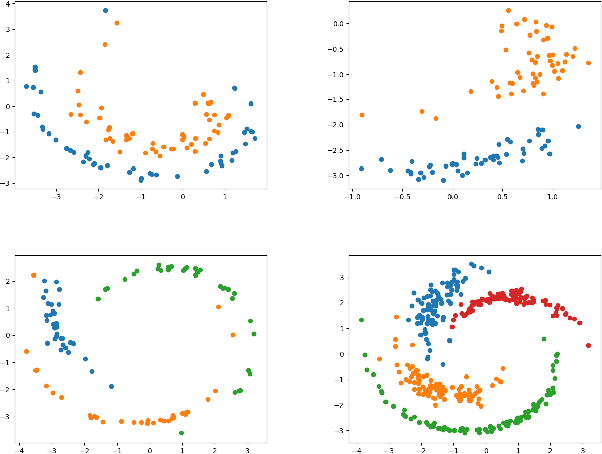
Clustering is one of the most fundamental and wide-spread techniques in exploratory data analysis. Yet, the basic approach to clustering has not really changed: a practitioner hand-picks a task-specific clustering loss to optimize and fit the given data to reveal the underlying cluster structure. Some types of losses---such as k-means, or its non-linear version: kernelized k-means (centroid based), and DBSCAN (density based)---are popular choices due to their good empirical performance on a range of applications. Although every so often the clustering output using these standard losses fails to reveal the underlying structure, and the practitioner has to custom-design their own variation. In this work we take an intrinsically different approach to clustering: rather than fitting a dataset to a specific clustering loss, we train a recurrent model that learns how to cluster. The model uses as training pairs examples of datasets (as input) and its corresponding cluster identities (as output). By providing multiple types of training datasets as inputs, our model has the ability to generalize well on unseen datasets (new clustering tasks). Our experiments reveal that by training on simple synthetically generated datasets or on existing real datasets, we can achieve better clustering performance on unseen real-world datasets when compared with standard benchmark clustering techniques. Our meta clustering model works well even for small datasets where the usual deep learning models tend to perform worse.