Masahito Ueda
Symbolic Equation Solving via Reinforcement Learning
Jan 24, 2024Abstract:Machine-learning methods are gradually being adopted in a great variety of social, economic, and scientific contexts, yet they are notorious for struggling with exact mathematics. A typical example is computer algebra, which includes tasks like simplifying mathematical terms, calculating formal derivatives, or finding exact solutions of algebraic equations. Traditional software packages for these purposes are commonly based on a huge database of rules for how a specific operation (e.g., differentiation) transforms a certain term (e.g., sine function) into another one (e.g., cosine function). Thus far, these rules have usually needed to be discovered and subsequently programmed by humans. Focusing on the paradigmatic example of solving linear equations in symbolic form, we demonstrate how the process of finding elementary transformation rules and step-by-step solutions can be automated using reinforcement learning with deep neural networks.
Law of Balance and Stationary Distribution of Stochastic Gradient Descent
Aug 13, 2023



Abstract:The stochastic gradient descent (SGD) algorithm is the algorithm we use to train neural networks. However, it remains poorly understood how the SGD navigates the highly nonlinear and degenerate loss landscape of a neural network. In this work, we prove that the minibatch noise of SGD regularizes the solution towards a balanced solution whenever the loss function contains a rescaling symmetry. Because the difference between a simple diffusion process and SGD dynamics is the most significant when symmetries are present, our theory implies that the loss function symmetries constitute an essential probe of how SGD works. We then apply this result to derive the stationary distribution of stochastic gradient flow for a diagonal linear network with arbitrary depth and width. The stationary distribution exhibits complicated nonlinear phenomena such as phase transitions, broken ergodicity, and fluctuation inversion. These phenomena are shown to exist uniquely in deep networks, implying a fundamental difference between deep and shallow models.
The Probabilistic Stability of Stochastic Gradient Descent
Mar 23, 2023



Abstract:A fundamental open problem in deep learning theory is how to define and understand the stability of stochastic gradient descent (SGD) close to a fixed point. Conventional literature relies on the convergence of statistical moments, esp., the variance, of the parameters to quantify the stability. We revisit the definition of stability for SGD and use the \textit{convergence in probability} condition to define the \textit{probabilistic stability} of SGD. The proposed stability directly answers a fundamental question in deep learning theory: how SGD selects a meaningful solution for a neural network from an enormous number of solutions that may overfit badly. To achieve this, we show that only under the lens of probabilistic stability does SGD exhibit rich and practically relevant phases of learning, such as the phases of the complete loss of stability, incorrect learning, convergence to low-rank saddles, and correct learning. When applied to a neural network, these phase diagrams imply that SGD prefers low-rank saddles when the underlying gradient is noisy, thereby improving the learning performance. This result is in sharp contrast to the conventional wisdom that SGD prefers flatter minima to sharp ones, which we find insufficient to explain the experimental data. We also prove that the probabilistic stability of SGD can be quantified by the Lyapunov exponents of the SGD dynamics, which can easily be measured in practice. Our work potentially opens a new venue for addressing the fundamental question of how the learning algorithm affects the learning outcome in deep learning.
What shapes the loss landscape of self-supervised learning?
Oct 02, 2022



Abstract:Prevention of complete and dimensional collapse of representations has recently become a design principle for self-supervised learning (SSL). However, questions remain in our theoretical understanding: When do those collapses occur? What are the mechanisms and causes? We provide answers to these questions by thoroughly analyzing SSL loss landscapes for a linear model. We derive an analytically tractable theory of SSL landscape and show that it accurately captures an array of collapse phenomena and identifies their causes. Finally, we leverage the interpretability afforded by the analytical theory to understand how dimensional collapse can be beneficial and what affects the robustness of SSL against data imbalance.
Three Learning Stages and Accuracy-Efficiency Tradeoff of Restricted Boltzmann Machines
Sep 02, 2022Abstract:Restricted Boltzmann Machines (RBMs) offer a versatile architecture for unsupervised machine learning that can in principle approximate any target probability distribution with arbitrary accuracy. However, the RBM model is usually not directly accessible due to its computational complexity, and Markov-chain sampling is invoked to analyze the learned probability distribution. For training and eventual applications, it is thus desirable to have a sampler that is both accurate and efficient. We highlight that these two goals generally compete with each other and cannot be achieved simultaneously. More specifically, we identify and quantitatively characterize three regimes of RBM learning: independent learning, where the accuracy improves without losing efficiency; correlation learning, where higher accuracy entails lower efficiency; and degradation, where both accuracy and efficiency no longer improve or even deteriorate. These findings are based on numerical experiments and heuristic arguments.
Exact Phase Transitions in Deep Learning
May 25, 2022
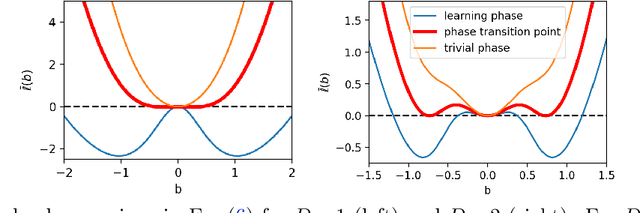
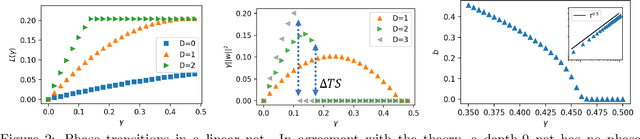
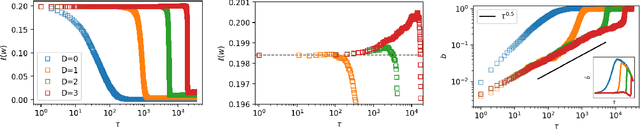
Abstract:This work reports deep-learning-unique first-order and second-order phase transitions, whose phenomenology closely follows that in statistical physics. In particular, we prove that the competition between prediction error and model complexity in the training loss leads to the second-order phase transition for nets with one hidden layer and the first-order phase transition for nets with more than one hidden layer. The proposed theory is directly relevant to the optimization of neural networks and points to an origin of the posterior collapse problem in Bayesian deep learning.
Stochastic Neural Networks with Infinite Width are Deterministic
Jan 30, 2022



Abstract:This work theoretically studies stochastic neural networks, a main type of neural network in use. Specifically, we prove that as the width of an optimized stochastic neural network tends to infinity, its predictive variance on the training set decreases to zero. Two common examples that our theory applies to are neural networks with dropout and variational autoencoders. Our result helps better understand how stochasticity affects the learning of neural networks and thus design better architectures for practical problems.
Interplay between depth of neural networks and locality of target functions
Jan 28, 2022



Abstract:It has been recognized that heavily overparameterized deep neural networks (DNNs) exhibit surprisingly good generalization performance in various machine-learning tasks. Although benefits of depth have been investigated from different perspectives such as the approximation theory and the statistical learning theory, existing theories do not adequately explain the empirical success of overparameterized DNNs. In this work, we report a remarkable interplay between depth and locality of a target function. We introduce $k$-local and $k$-global functions, and find that depth is beneficial for learning local functions but detrimental to learning global functions. This interplay is not properly captured by the neural tangent kernel, which describes an infinitely wide neural network within the lazy learning regime.
SGD May Never Escape Saddle Points
Jul 25, 2021



Abstract:Stochastic gradient descent (SGD) has been deployed to solve highly non-linear and non-convex machine learning problems such as the training of deep neural networks. However, previous works on SGD often rely on highly restrictive and unrealistic assumptions about the nature of noise in SGD. In this work, we mathematically construct examples that defy previous understandings of SGD. For example, our constructions show that: (1) SGD may converge to a local maximum; (2) SGD may escape a saddle point arbitrarily slowly; (3) SGD may prefer sharp minima over the flat ones; and (4) AMSGrad may converge to a local maximum. Our result suggests that the noise structure of SGD might be more important than the loss landscape in neural network training and that future research should focus on deriving the actual noise structure in deep learning.
A Convergent and Efficient Deep Q Network Algorithm
Jun 29, 2021



Abstract:Despite the empirical success of the deep Q network (DQN) reinforcement learning algorithm and its variants, DQN is still not well understood and it does not guarantee convergence. In this work, we show that DQN can diverge and cease to operate in realistic settings. Although there exist gradient-based convergent methods, we show that they actually have inherent problems in learning behaviour and elucidate why they often fail in practice. To overcome these problems, we propose a convergent DQN algorithm (C-DQN) by carefully modifying DQN, and we show that the algorithm is convergent and can work with large discount factors (0.9998). It learns robustly in difficult settings and can learn several difficult games in the Atari 2600 benchmark where DQN fail, within a moderate computational budget. Our codes have been publicly released and can be used to reproduce our results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge