A Convergent and Efficient Deep Q Network Algorithm

Despite the empirical success of the deep Q network (DQN) reinforcement learning algorithm and its variants, DQN is still not well understood and it does not guarantee convergence. In this work, we show that DQN can diverge and cease to operate in realistic settings. Although there exist gradient-based convergent methods, we show that they actually have inherent problems in learning behaviour and elucidate why they often fail in practice. To overcome these problems, we propose a convergent DQN algorithm (C-DQN) by carefully modifying DQN, and we show that the algorithm is convergent and can work with large discount factors (0.9998). It learns robustly in difficult settings and can learn several difficult games in the Atari 2600 benchmark where DQN fail, within a moderate computational budget. Our codes have been publicly released and can be used to reproduce our results.

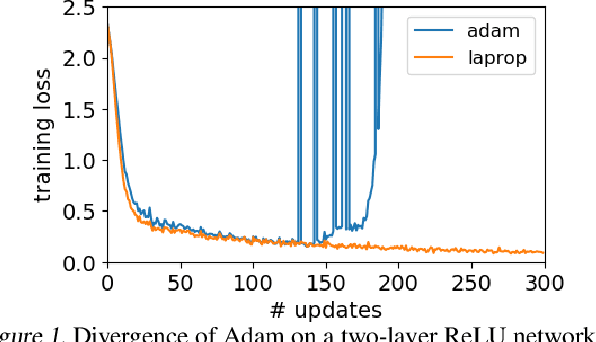
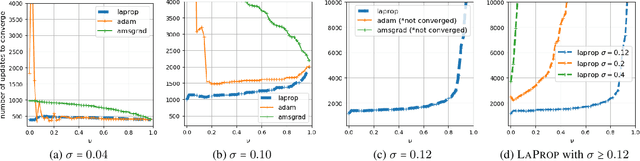
LaProp: a Better Way to Combine Momentum with Adaptive Gradient

Identifying a divergence problem in Adam, we propose a new optimizer, LaProp, which belongs to the family of adaptive gradient descent methods. This method allows for greater flexibility in choosing its hyperparameters, mitigates the effort of fine tuning, and permits straightforward interpolation between the signed gradient methods and the adaptive gradient methods. We bound the regret of LaProp on a convex problem and show that our bound differs from the previous methods by a key factor, which demonstrates its advantage. We experimentally show that LaProp outperforms the previous methods on a toy task with noisy gradients, optimization of extremely deep fully-connected networks, neural art style transfer, natural language processing using transformers, and reinforcement learning with deep-Q networks. The performance improvement of LaProp is shown to be consistent, sometimes dramatic and qualitative.

Deep Reinforcement Learning Control of Quantum Cartpoles

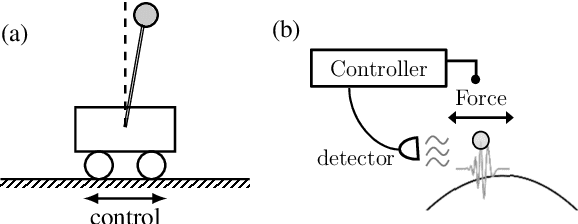
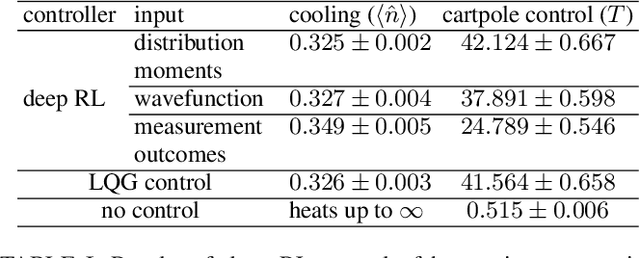
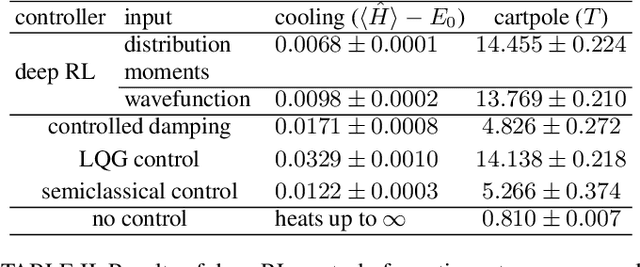
We generalize a standard benchmark of reinforcement learning, the classical cartpole balancing problem, to the quantum regime by stabilizing a particle in an unstable potential through measurement and feedback. We use the state-of-the-art deep reinforcement learning to stabilize the quantum cartpole and find that our deep learning approach performs comparably to or better than other strategies in standard control theory. Our approach also applies to measurement-feedback cooling of quantum oscillators, showing the applicability of deep learning to general continuous-space quantum control.