LaProp: a Better Way to Combine Momentum with Adaptive Gradient
Paper and Code
Feb 12, 2020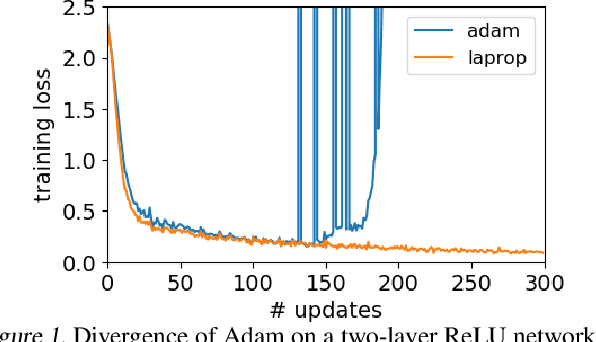


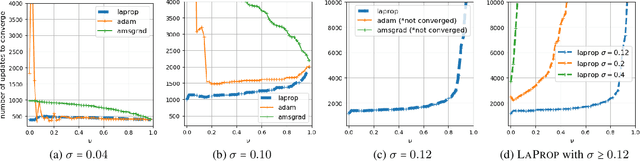
Identifying a divergence problem in Adam, we propose a new optimizer, LaProp, which belongs to the family of adaptive gradient descent methods. This method allows for greater flexibility in choosing its hyperparameters, mitigates the effort of fine tuning, and permits straightforward interpolation between the signed gradient methods and the adaptive gradient methods. We bound the regret of LaProp on a convex problem and show that our bound differs from the previous methods by a key factor, which demonstrates its advantage. We experimentally show that LaProp outperforms the previous methods on a toy task with noisy gradients, optimization of extremely deep fully-connected networks, neural art style transfer, natural language processing using transformers, and reinforcement learning with deep-Q networks. The performance improvement of LaProp is shown to be consistent, sometimes dramatic and qualitative.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge