Exact Phase Transitions in Deep Learning

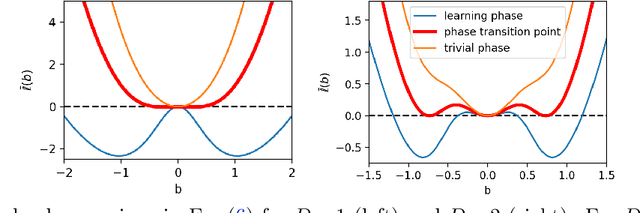
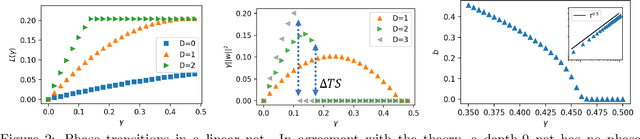
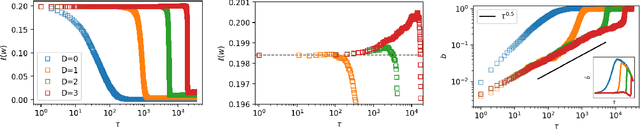
This work reports deep-learning-unique first-order and second-order phase transitions, whose phenomenology closely follows that in statistical physics. In particular, we prove that the competition between prediction error and model complexity in the training loss leads to the second-order phase transition for nets with one hidden layer and the first-order phase transition for nets with more than one hidden layer. The proposed theory is directly relevant to the optimization of neural networks and points to an origin of the posterior collapse problem in Bayesian deep learning.