Interplay between depth of neural networks and locality of target functions

It has been recognized that heavily overparameterized deep neural networks (DNNs) exhibit surprisingly good generalization performance in various machine-learning tasks. Although benefits of depth have been investigated from different perspectives such as the approximation theory and the statistical learning theory, existing theories do not adequately explain the empirical success of overparameterized DNNs. In this work, we report a remarkable interplay between depth and locality of a target function. We introduce $k$-local and $k$-global functions, and find that depth is beneficial for learning local functions but detrimental to learning global functions. This interplay is not properly captured by the neural tangent kernel, which describes an infinitely wide neural network within the lazy learning regime.

Logarithmic landscape and power-law escape rate of SGD

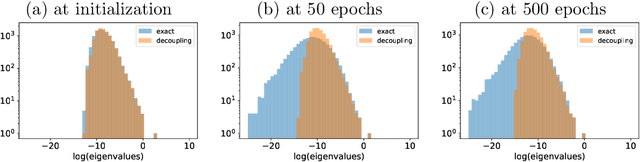
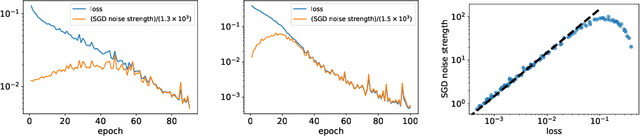
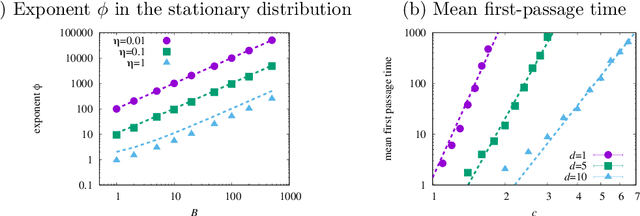
Stochastic gradient descent (SGD) undergoes complicated multiplicative noise for the mean-square loss. We use this property of the SGD noise to derive a stochastic differential equation (SDE) with simpler additive noise by performing a non-uniform transformation of the time variable. In the SDE, the gradient of the loss is replaced by that of the logarithmized loss. Consequently, we show that, near a local or global minimum, the stationary distribution $P_\mathrm{ss}(\theta)$ of the network parameters $\theta$ follows a power-law with respect to the loss function $L(\theta)$, i.e. $P_\mathrm{ss}(\theta)\propto L(\theta)^{-\phi}$ with the exponent $\phi$ specified by the mini-batch size, the learning rate, and the Hessian at the minimum. We obtain the escape rate formula from a local minimum, which is determined not by the loss barrier height $\Delta L=L(\theta^s)-L(\theta^*)$ between a minimum $\theta^*$ and a saddle $\theta^s$ but by the logarithmized loss barrier height $\Delta\log L=\log[L(\theta^s)/L(\theta^*)]$. Our escape-rate formula explains an empirical fact that SGD prefers flat minima with low effective dimensions.

On Minibatch Noise: Discrete-Time SGD, Overparametrization, and Bayes

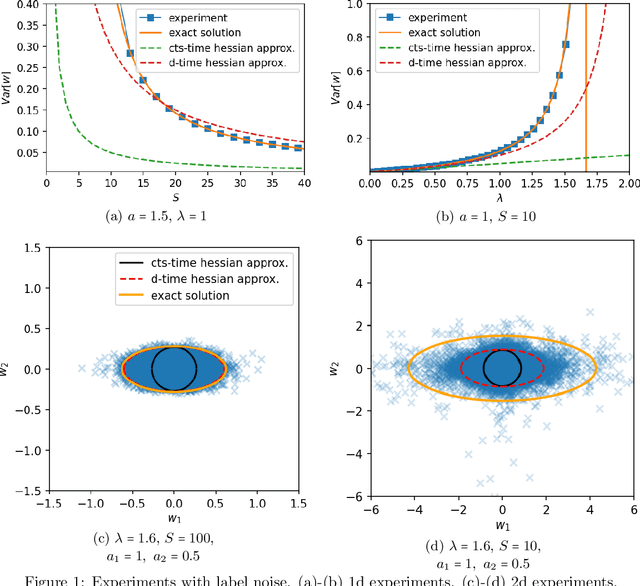
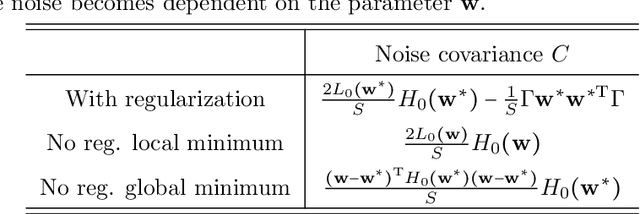
The noise in stochastic gradient descent (SGD), caused by minibatch sampling, remains poorly understood despite its enormous practical importance in offering good training efficiency and generalization ability. In this work, we study the minibatch noise in SGD. Motivated by the observation that minibatch sampling does not always cause a fluctuation, we set out to find the conditions that cause minibatch noise to emerge. We first derive the analytically solvable results for linear regression under various settings, which are compared to the commonly used approximations that are used to understand SGD noise. We show that some degree of mismatch between model and data complexity is needed in order for SGD to "cause" a noise, and that such mismatch may be due to the existence of static noise in the labels, in the input, the use of regularization, or underparametrization. Our results motivate a more accurate general formulation to describe minibatch noise.

Improved generalization by noise enhancement

Recent studies have demonstrated that noise in stochastic gradient descent (SGD) is closely related to generalization: A larger SGD noise, if not too large, results in better generalization. Since the covariance of the SGD noise is proportional to $\eta^2/B$, where $\eta$ is the learning rate and $B$ is the minibatch size of SGD, the SGD noise has so far been controlled by changing $\eta$ and/or $B$. However, too large $\eta$ results in instability in the training dynamics and a small $B$ prevents scalable parallel computation. It is thus desirable to develop a method of controlling the SGD noise without changing $\eta$ and $B$. In this paper, we propose a method that achieves this goal using ``noise enhancement'', which is easily implemented in practice. We expound the underlying theoretical idea and demonstrate that the noise enhancement actually improves generalization for real datasets. It turns out that large-batch training with the noise enhancement even shows better generalization compared with small-batch training.

Is deeper better? It depends on locality of relevant features

It has been recognized that a heavily overparameterized artificial neural network exhibits surprisingly good generalization performance in various machine-learning tasks. Recent theoretical studies have made attempts to unveil the mystery of the overparameterization. In most of those previous works, the overparameterization is achieved by increasing the width of the network, while the effect of increasing the depth has been less well understood. In this work, we investigate the effect of increasing the depth within an overparameterized regime. To gain an insight into the advantage of depth, we introduce local and global labels as abstract but simple classification rules. It turns out that the locality of the relevant feature for a given classification rule plays an important role; our experimental results suggest that deeper is better for local labels, whereas shallower is better for global labels. We also compare the results of finite networks with those of the neural tangent kernel (NTK), which is equivalent to an infinitely wide network with a proper initialization and an infinitesimal learning rate. It is shown that the NTK does not correctly capture the depth dependence of the generalization performance, which indicates the importance of the feature learning, rather than the lazy learning.